Condition de Hölder
|
Read other articles:

H.Rohadi WidodoS.P Wakil Bupati KaranganyarMasa jabatan15 Desember 2013 – 15 Desember 2018PresidenSusilo Bambang Yudhoyono Joko WidodoGubernurGanjar Pranowo PendahuluParyonoPenggantiRober Christanto Informasi pribadiLahir(1973-04-01)1 April 1973KaranganyarMeninggal24 Januari 2023(2023-01-24) (umur 49)SemarangPartai politikPartai Keadilan SejahteraSunting kotak info • L • B H. Rohadi Widodo, S.P (1 April 1973 – 24 Januari 2023) adalah Wakil Bupati ...

Roman Catholic church in Laguna, Philippines Church in Laguna, PhilippinesPila ChurchSt. Anthony of Padua ParishNational Shrine of St. Anthony of PaduaSantuario Nacional de San Antonio de Padua (Spanish)Pambansang Dambana ng San Antonio de Padua (Filipino)Church facade in 2015Pila ChurchShow map of LagunaPila ChurchShow map of LuzonPila ChurchShow map of Philippines14°14′02″N 121°21′52″E / 14.233958°N 121.364398°E / 14.233958; 121.364398LocationPo...

Cette page présente les armoiries (figures et blasonnements) des différentes branches et des membres issus de la Maison Grimaldi et de la famille princière de Monaco. Armorial Figure Nom de la branche familiale ou du personnage, et blasonnement Branche des princes de Monaco. Fuselé d'argent et de gueules. Tenants : Deux moines de l’Ordre des frères mineurs, chevelus, barbus et chaussés, portant chacun une épée levée, debout sur une banderole.Les moines soutenant le bouclier é...

1982 Italian giallo film directed by Lucio Fulci Psycho Ripper redirects here. For the professional wrestler, see Psyco Ripper. The New York RipperItalian theatrical release poster by Enzo Sciotti[1]Directed byLucio FulciScreenplay by Gianfranco Clerici Lucio Fulci Vincenzo Mannino Dardano Sacchetti[1] Story by Gianfranco Clerici Lucio Fulci Vincenzo Mannino[1] Produced byFabrizio De Angelis[1]Starring Jack Hedley Paolo Malco Almanta Suska Alexandra Delli Colli...

Eleanor & Park Sampul edisi IndonesiaPengarangRainbow RowellNegaraAmerika SerikatBahasaInggrisGenreRomansaPenerbitOrion BooksTanggal terbitApril 2012Jenis mediaPrint (Hardback), AudiobookHalaman333ISBNISBN 1250012570 Eleanor & Park adalah sebuah novel debut karya Rainbow Rowell. Ceritanya mengikuti narasi ganda dari Eleanor dan Park, dua orang aneh yang tinggal di Omaha, Nebraska dari tahun 1986 hingga 1987. Eleanor, seorang gadis gemuk berusia 16 tahun dengan rambut merah k...

American art historian For the actress, see Christiane Paul. Christiane Paul is Curator of Digital Art at the Whitney Museum of American Art and professor emerita in the School of Media Studies at The New School. She is the author of the book Digital Art, which is part of the 'World of Art' series published by Thames & Hudson.[1] Education Paul received both her MA and PhD from the University of Düsseldorf in North Rhine-Westphalia, Germany.[2] Career In 2016, Paul was th...

Fernando Amárica Medina Busto en homenaje de Fernando de Amárica en los jardines del Museo de Bellas Artes de ÁlavaInformación personalNacimiento 1 de junio de 1866Vitoria, EspañaFallecimiento 6 de noviembre de 1956 (91 años)Vitoria, EspañaSepultura Cementerio de Santa Isabel Nacionalidad EspañolaEducaciónEducado en Universidad de Valladolid Alumno de Joaquín Sorolla Información profesionalÁrea PinturaMovimiento Impresionismo[editar datos en Wikidata] Fernando Amárica M...

Battaglia di Marj al-Suffarparte delle invasioni mongole della SiriaLa battaglia di Marj al-Saffar nel contesto delle offensive mongole nel Levante arabo, 1299-1300Data20-22 aprile 1303 LuogoGhabaghib, Siria Esitodecisiva vittoria dei mamelucchi Schieramenti Sultanato mamelucco Ilkhanato Regno armeno di Cilicia[1] ComandantiBaybars IIal-Nasir MuhammadQutlugh-ShahAitone II d'Armenia Effettivi40000 uomini80000 uomini Voci di battaglie presenti su Wikipedia Manuale La battaglia di Marj a...
2020年夏季奥林匹克运动会科索沃代表團科索沃国旗IOC編碼KOSNOC科索沃奧林匹克委員會網站www.noc-kosovo.org(英文)(阿爾巴尼亞文)(塞爾維亞文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員11參賽項目6个大项旗手开幕式:阿基爾·賈科瓦(英语:Akil Gjakova)和瑪琳達·開爾門蒂(柔道)[1]闭幕式�...

Pour les articles homonymes, voir Comté de McHenry. Cet article est une ébauche concernant le Dakota du Nord. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Comté de McHenry(McHenry County) Le palais de justice de Towner, siège du comté. Administration Pays États-Unis État Dakota du Nord Chef-lieu Towner Démographie Population 5 345 hab. (2020) Densité 1,1 hab./km2 Géographie Coordonné...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

American artist Bessie Niemeyer MarshallBornSarah Elizabeth Niemeyer(1884-12-25)December 25, 1884Portsmouth, VirginiaDiedFebruary 14, 1960(1960-02-14) (aged 75)Portsmouth, VirginiaNationalityAmericanKnown forPainting (watercolor) Bessie Niemeyer Marshall was an American botanical illustrator known for her watercolor paintings of the wildflowers of Lee Memorial Park. Her artwork documented the variety of plant species being preserved in Lee Memorial Park, a Works Progress Administrat...

لمعانٍ أخرى، طالع حزب الله (توضيح). ميّز عن حزب الله اللبناني. حزب الله هو حزب يمني أنشأهمحمد محمود الزبيري عام 1963 في الجمهورية العربية اليمنية خلال فترة الصراع الملكي الجمهوري بعد قيام ثورة 26 سبتمبر وكان هدفه قيام دولة اليمن الإسلامية، واستمر فاعلاً حتى اغتيا�...

Trails in MinneapolisMidtown Greenway is one of many shared-use paths in Minneapolis for bicyclists and pedestrians.TypeShared-use pathsHiking trailsCross-country ski trailsPedestrian areasLong-distance trailsLocationMinneapolis, Minnesota, United States Minneapolis is often considered one of the top biking and walking cities in the United States due to its vast network of trails and dedicated pedestrian areas. In 2020, Walk Score rated Minneapolis as 13th highest among cities over 200,000 p...

Bagian dari seriPendidikan di Indonesia Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi Republik Indonesia Pendidikan anak usia dini TK RA KB Pendidikan dasar (kelas 1–6) SD MI Paket A Pendidikan dasar (kelas 7–9) SMP MTs Paket B Pendidikan menengah (kelas 10–12) SMA MA SMK MAK SMA SMTK SMAK Utama Widya Pasraman Paket C Pendidikan tinggi Perguruan tinggi Akademi Akademi komunitas Institut Politeknik Sekolah tinggi Universitas Lain-lain Madrasah Pesantren Sekolah alam Sekolah ru...

British socialist organisation founded in 1884 For other organisations known by the same name, see § Fabianism outside the United Kingdom. The Fabian SocietyAbbreviationFSFormation4 January 1884; 140 years ago (1884-01-04)Legal statusUnincorporated membership associationPurposeTo promote greater equality of power, wealth and opportunity; the value of collective action and public service; an accountable, tolerant and active democracy; citizenship, liberty and human righ...

Indian actor and comedian (1961–2021) Not to be confused with Vivek Oberoi. VivekVivek in 2019BornVivekanandan[1](1961-11-19)19 November 1961Sankarankovil, Tenkasi District, Tamil Nadu, IndiaDied17 April 2021(2021-04-17) (aged 59)Chennai, Tamil Nadu, IndiaAlma materAmerican College, MaduraiOccupation(s)Actor, Comedian, Television personality, Playback singer, Lyricist, Social activistYears active1987 - 2021Height172 cm (5 ft 8 in)SpouseArulselviChildren...

В Википедии есть статьи о других людях с такой фамилией, см. Сикорский. Анатолий Сергеевич Сикорский Рождение 15 июля 1956(1956-07-15) (67 лет)Корчовка Партия Либерально-демократическая партия России Медиафайлы на Викискладе Анатолий Сергеевич Сикорский (род. 15 июля 1956, Корчов�...
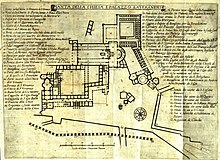
Election of Pope Celestine II Papal electionSeptember 1143Dates and location26 September 1143Archbasilica of St. John Lateran, RomeKey officialsDeanCorrado Demetri della SuburraProtopriestGerardo CaccianemiciProtodeaconGregorio TarquiniElected popeGuido di CastelloName taken: Celestine II← 11301144 → The 1143 papal election followed the death of Pope Innocent II and resulted in the election of Pope Celestine II. Plan of the medieval Lateran Basilica Election of Celestine II Pope...

Football clubDoxa VyronasFull nameΠοδοσφαιρικός Αθλητικός Όμιλος Δόξα Βύρωνα(Football Athletic Club Doxa Vyronas)Nickname(s)Doxa (Glory)Founded1945; 79 years ago (1945)GroundVyronas National StadiumCapacity4,500ChairmanIlias SaltantzoglouManagerLoukas RopasLeagueAthens FCA First Division2023–24Athens FCA First Division (2nd Group), 10thWebsiteClub website Home colours Away colours Doxa Vyronas (Greek: Π.Α.Ο. Δόξα Βύρωνος;...


![{\displaystyle C_{a}=1/[e(1-a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af12b4c00eec9558daf972bba84188f030b6e95b)

















![{\displaystyle [0,1]\rightarrow [0,1]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb92c9eddacbbab731ad54faec51ce8fd275ac5)

