Calcul de la date de PûÂques selon la mûˋthode de Conway
|
Read other articles:

The Water DivinerPoster rilis teatrikalSutradaraRussell CroweProduser Troy Lum Andrew Mason Keith Rodger Ditulis oleh Andrew Anastasios Andrew Knight Pemeran Russell Crowe Olga Kurylenko YáÝlmaz Erdoáan Jacqueline McKenzie Penata musikDavid HirschfelderSinematograferAndrew LesniePenyuntingMatt VillaPerusahaanproduksi RatPac Entertainment Seven Network Australia Hopscotch Features Fear of God Films Distributor Entertainment One Films (Australia) Universal Pictures Australia (Australia) ...

DinoNama asalLee Chan (šÇš¯˜)Lahir11 Februari 1999 (umur 25)Iksan, Jeollabuk-do, Korea SelatanPekerjaanRapper, penari, penyanyiTahun aktif2015ãsekarang Lee Chan (šÇš¯˜) (lahir 11 Februari 1999) atau yang lebih dikenal dengan nama panggung Dino, adalah seorang rapper, penyanyi dan penari asal Korea Selatan. Ia adalah anggota grup vokal laki-laki SEVENTEEN.[1] Ia berperan sebagai koreografer di grup SEVENTEEN bersama dengan Hoshi. Referensi ^ [SEVENTEEN Ó¯ÀÌÙñã´...

Village in Ardabil, IranKhan Kandi ÄÛÄÏì ììÄ₤ìvillageKhan KandiCoordinates: 38ô¯55ãý17ã°N 48ô¯03ãý25ã°E / 38.92139ô¯N 48.05694ô¯E / 38.92139; 48.05694Country IranProvinceArdabilCountyGermiBakhshCentralRural DistrictOjarud-e GharbiElevation1,664 m (5,459 ft)Population (2006) ã Total18Time zoneUTC+3:30 (IRST) ã Summer (DST)UTC+4:30 (IRDT)Area code655 Khan Kandi (Persian: ÄÛÄÏì ììÄ₤ì, also Romanized as Khán Kandá¨)&...

Russian civil society organization Anti-War Committee of Russia ÅŧîÅ¡ÅýŃÅçŧŧîÅ¿ ŤŃťšîÅçî ŠŃîîÅ¡Å¡AbbreviationAWCR (English)ÅKÅ (Russian)Founders Mikhail Khodorkovsky Lyubov Sobol Mikhail Kasyanov Garry Kasparov Sergei Guriev Vladimir Kara-Murza Dmitry Gudkov Boris Zimin Mikhail Kokorich Evgeny Chichvarkin Sergei Aleksashenko Alexander Nevzorov FoundedFebruary 27, 2022; 2 years ago (2022-02-27)IdeologyAnti-PutinismAnti-warPolitical positionBig tentNati...

Dolf JoekesDolf Joekes pada tahun 1930.Lahir5 Mei 1884Buo, Lintau Buo, Tanah DatarMeninggal1 April 1962's-GravenhagePekerjaanPolitisi Adolf Marcus Dolf Joekes (5 Mei 1884 – 1 April 1962) adalah politikus Belanda. Riwayat hidup Dolf Joekes belajar Ilmu Hukum di Universitas Leiden pada tahun 1908. Pada tahun 1911, ia mempelajari Ilmu Tata Negara di perguruan tinggi yang sama. Joekes memulai karier parlemennya pada bulan September 1925 sebagai anggota fraksi Perhimpunan Demokrat...

Elvis Presley fan This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: June Juanico ã news ôñ newspapers ôñ books ôñ scholar ôñ JSTOR (October 2021) (Learn how and when to remove this template message) J...

Mordanocomune LocalizzazioneStato Italia Regione Emilia-Romagna Cittû metropolitana Bologna AmministrazioneSindacoNicola Tassinari (Partito Democratico) dal 27-5-2019 TerritorioCoordinate44ô¯24ãýN 11ô¯49ãýE / 44.4ô¯N 11.816667ô¯E44.4; 11.816667ÿ£¢ (Mordano)Coordinate: 44ô¯24ãýN 11ô¯49ãýE / 44.4ô¯N 11.816667ô¯E44.4; 11.816667ÿ£¢ (Mordano) Altitudine21 m s.l.m. Superficie21,45 kmôý Abitanti4 582[2] (31-10-2...

Geshe Sonam Rinchen reads a Buddhist text at home in Dharamsala in 2008 (photo by Peter Aronson) Geshe Sonam Rinchen (1933ã2013) was a Tibetan Buddhist scholar, writer, and teacher. He was born in Trehor region of Kham in Eastern Tibet in 1933. He died in Dharamshala, India, on 5 October 2013. In 1945, he joined Dhargyey Monastery and entered the monastic university of Sera in Lhasa in 1952, where he studied until he was forced to flee Tibet in 1959. In India, he completed his studies for t...
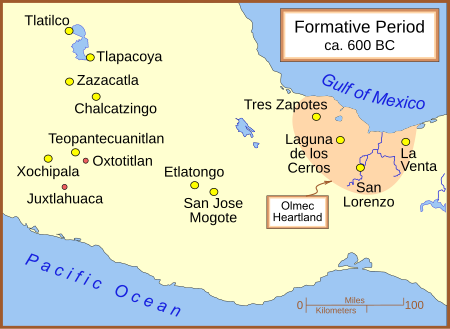
For the town by this name in Oaxaca, see Santiago Juxtlahuaca. Painting 1 from Juxtlahuaca. Juxtlahuaca Spanish pronunciation: [xuòtè˜aùwaka] is a cave and archaeological site in the Mexican state of Guerrero containing murals linked to the Olmec motifs and iconography. Along with the nearby OxtotitlûÀn cave, Juxtlahuaca walls contain the earliest sophisticated painted art known in Mesoamerica,[1] and only known example of non-Maya deep cave art in Mesoamerica.[2] Th...

NXT Women's ChampionshipDesain pertama Sabuk NXT Women's Championship.InformasiJuara saat iniLyra ValkyriaTanggal dimenangkan24 Oktober 2023Tanggal dibentuk5 April 2013PromotorWWEMerekNXTStatistikPemegang pertamaPaige[1]Pemegang terbanyakSemua (1 kali)Pemegang terlamaPaige (308 hari)Pemegang tersingkatSasha Banks (192 hari)Pemegang tertuaAsuka (34 tahun, 188 hari)Pemegang termudaPaige (20 tahun, 308 hari)Pemegang terberatAsuka 137 lbs (62 kg)Pemegang paling ringanS...

Ì₤ÌÇÍð¡¿ôñÓÝ°ÌÇÒÓ£ÇÍËÅÀţŃÅÝŃÅÇůŧ ÅšţŃîÅçÅýÅ¡îSlobodan MiloéÀeviá ÍÌ₤ÌÍʨÒÓÍ ÝÍͧӘ˜3ð££Ì£Ó£ð££Ì1997Í¿Ç7Ì23ÌËã2000Í¿Ç10Ì7ÌËÌ£ÓÌÍÊÒÑôñÍÙÒÍËÒ¨ÓݰͯôñÍ¡ÌÌÓ£ÇÍËÍð££ð§Í ¯ôñÍˋÍˋÍËÿ¥ÒÝÒ₤Ùÿ¥Zoran Liliáÿ¥Ó£Ïð££Ìýð¥Ì₤ÌÍʨôñÓÏð£ÍƒÍ¯¥Í₤Ó˜˜1ð££ÍÀͯӣÇð¤Ì£Ó£ð££Ì1991Í¿Ç1Ì11ÌË[Ì°´]ã1997Í¿Ç7Ì23ÌËÌ£Ó̓ñÌÍÊð¤˜ôñÌ°§ÒÝÒ₤¤Ó£ÇÍËÿ¥ÒÝÒ₤Ùÿ¥Dragutin Zelenoviáÿ¥ÌÍÊÌ¥ôñÍÒËÓ£ÇÍËÿ¥ÒÝÒ₤Ùÿ¥Radoman Bo...

ì ÄÏììì ììì Michael Caine ì Ä¿ììì ÄÏĈ ÄÇÄÛÄçìÄˋ ÄÏÄ°ì ÄÏìììÄÏÄ₤Äˋ ì ìÄÝìÄ° ĘìÄýìì ì ììììììĈ ÄÏìì ììÄÏÄ₤ 14 ì ÄÏÄÝÄ° 1933 (ÄÏìÄ¿ì ÄÝ 91 Ä°ìÄˋ)ììÄ₤ìÄ ÄËìĘìĈÄÝÄÏ ÄÏìÄËìÄÏì Äˋ ììÄ₤ÄýÄÝÄ Ä´ìÄÝìÄÇÄÏìÄÝ (ÄÏìÄ¿ìÄ₤ 1960ãÄÏìÄ¿ìÄ₤ 1970) ÄÏìĘìÄ°ìÄˋ ÄÏìì ì ììÄˋ ÄÏìì ĈÄÙÄ₤Äˋ ÄÏìÄñìì ìÄÏìÄ´:ÄÏìÄÏÄÝĈìÄÏÄ¿m=2.26I ÄÏìÄýìĘÄˋ ÄÇÄÏììÄÝÄÏ ììì (8 ììÄÏìÄÝ 1973ã) ÄËÄÛìÄˋ ìÄÈÄÛìÄÏĈ İĈÄÏììì ììì ÄÏìÿ¢§...

2018 book by Ben Rhodes The World as It Is AuthorBen RhodesCountryUnited StatesLanguageEnglishSubjectPresidency of Barack ObamaGenreMemoirPublishedJune 5, 2018PublisherRandom HousePages480ISBN978-0-5255-0935-6 The World as It Is is a memoir by Ben Rhodes, a former White House staffer and longtime adviser to former U.S. President Barack Obama. The book was released by Random House on June 5, 2018. It includes a recounting of many important events during Obama's two terms as President. It also ...

Cet article est une ûˋbauche concernant le sport automobile. Vous pouvez partager vos connaissances en lãamûˋliorant (comment ?) selon les recommandations des projets correspondants. Rod MillenBiographieNaissance 22 mars 1951 (73 ans)Newport BeachNationalitûˋ nûˋo-zûˋlandaiseActivitûˋ Pilote de rallyeAutres informationsSport Rallye automobilemodifier - modifier le code - modifier Wikidata Rodney K. Rod Millen, nûˋ le 22 mars 1951, est un ancien pilote automobile ûˋclectique, de r...

Manuel GonzûÀlez de Candamo e Iriarte Presiden Junta Pemerintahan Sementara PeruMasa jabatan20 Maret 1895 ã 8 September 1895PendahuluAndrûˋs Avelino CûÀceresPenggantiNicolûÀs de PiûˋrolaPresiden PeruMasa jabatan8 September 1903 ã 7 Mei 1904PendahuluEduardo Lû°pez de RomaûÝaPenggantiSerapio Calderû°n Informasi pribadiLahir(1841-07-14)14 Juli 1841Lima, PeruMeninggal7 Mei 1904(1904-05-07) (umur 62)Arequipa, PeruKebangsaanPeruPartai politikPartido CivilSuami/istriTeresa...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Decree on Land ã news ôñ newspapers ôñ books ôñ scholar ôñ JSTOR (January 2017) (Learn how and when to remove this message) Main article: Soviet Decree Decree on Land title page The Decree on Land (Russian: ÅÅçŤîÅçîî Ń ÅñÅçťţîÈ), written by Vladimir Lenin, ...

Quasi famosiPatrick Fugit e Kate Hudson in una scena del filmTitolo originaleAlmost Famous Paese di produzioneStati Uniti d'America Anno2000 Durata122 min (versione originale)161 min (versione Untitled) Generecommedia, drammatico, musicale RegiaCameron Crowe SceneggiaturaCameron Crowe ProduttoreCameron Crowe, Ian Bryce Casa di produzioneColumbia Pictures, DreamWorks Pictures, Vinyl Films FotografiaJohn Toll MontaggioJoe Hutshing, Saar Klein Effetti specialiJohn Frazier, Ed Jones Music...

ÐÐÛÒ´ð¤Ð₤ÌÊÒ´¥Í₤ҧЈÍÒÌÓÛÐÍ¤Í ¡ÐÍ ´ÐÓʤÐÐÐÎÐЈÐÐÐð¡ÍÍÐÏÐÐ Í¤Í ¡ÐÒ¢§Í ÐÐÎÒ´ð¤ÐÛð¢ÀÕ ¥ÌÏÍð¡Ð¨ÐÍÍÐÐ ÐÐÐÿ¥ÐÐÛÐаÐИХÐÐÛð§¢ÐÌ¿ÿ¥Í¤Í ¡ÌÊÓÇÂ?: ÐÎÐˋХТХÐпÐÝÐÐÐХШ ã ÐÐËХп ôñ Ì¡ÓÝ ôñ пШÐˋÐ¥ ôñ CiNii ôñ J-STAGE ôñ NDL ôñ dlib.jp ôñ СÐÈÐаÐçХРôñ TWL (2023Í¿Ç2Ì) ÐÎÐˋХТХÐпÐÝÐÐÐХШÿ¢§...

Family of philosophical views For the negative mental attitude, see pessimism. Melancholy by Domenico Fetti (1612). Death, suffering and meaninglessness are the main themes of philosophical pessimism. Philosophical pessimism is a family of philosophical views that assign a negative value to life or existence. Philosophical pessimists commonly argue that the world contains an empirical prevalence of pains over pleasures, that existence is ontologically or metaphysically adverse to living being...

Monetary union formed by Sweden and Denmark on May 5, 1873 Scandinavian Monetary UnionDen Skandinaviske Mû¡ntunion (Danish) Den skandinaviske myntunionen (Norwegian)Skandinaviska Myntunionen (Swedish)Two golden 20 kr coins, with identical weight and composition. The coin to the left is Swedish and the right one is Danish.UnitUnitkrone/kronaPluralkroner/kronorSymbolkr.DenominationsSubunit 1⁄100û¡re/ûÑrePlural û¡re/ûÑreû¡re/ûÑre (singular and plural)...