Read other articles:

Hari KemenanganPrajurit Angkatan Bersenjata Turki selama parade Hari Kemenangan, 30 Agustus 2007.Nama resmiZafer Bayramıcode: tr is deprecated   (Turkish)Nama lainHari Angkatan Bersenjata TurkiTiga Puluh AgustusDirayakan oleh Turkey Siprus UtaraJenisNasionalMaknaHari pada tahun 1922 Pertempuran Dumlupınar dimenangkan oleh tentara TurkiPerayaanParade militer, aerobatik demonstrasi, konser, acara di sekolah militerTanggal30 AgustusFrekuensitahunan Hari Kemenangan (Turki: Z...

Borgo d'Ale commune di Italia Tempat categoria:Articles mancats de coordenades Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Vercelli NegaraItalia Ibu kotaBorgo d'Ale PendudukTotal2.207  (2023 )GeografiLuas wilayah39,57 km² [convert: unit tak dikenal]Ketinggian242 m Berbatasan denganAlice Castello Azeglio Bianzè Cossano Canavese Maglione Moncrivello Settimo Rottaro Tronzano Vercellese Viverone Borgomasino SejarahSanto pelindungMikhael Informasi tamba...

Former railway station in England Lordship LaneLordship Lane Station, Dulwich, by Camille PissarroLocationEast DulwichLocal authorityMetropolitan Borough of CamberwellNumber of platforms2Railway companiesOriginal companyLondon, Chatham and Dover RailwayPre-groupingSouth Eastern and Chatham RailwayPost-groupingSouthern Railway British RailwaysKey dates1 September 1865Opened1 January 1917closed1 March 1919reopened22 May 1944closed4 March 1946reopened20 September 1954ClosedOther information ...

Physique du solideThéorie des bandes : cas d'un semi-conducteur.Partie de PhysiqueObjet Matière solidemodifier - modifier le code - modifier Wikidata La physique du solide est l'étude des propriétés fondamentales des matériaux solides, cristallins – par exemple la plupart des métaux –, ou amorphes – par exemple les verres – en partant autant que possible des propriétés à l'échelle atomique (par exemple la fonction d'onde électronique) pour remonter aux propriétés à...

Brian Goodwin pada 1992 Brian Carey Goodwin (25 Maret 1931 – 15 Juli 2009) adalah seorang matematikawan dan biologis asal Kanada, Profesor Emeritus di Open University dan pendiri biologi teoretiakl dan biomatematika. Ia mengenalkan pemakaian sistem kompleks dan model generatif dalam biologi perkembangan. Publikasi Buku 1963. Temporal Organization in Cells Academic Press, London 1963, ISBN 1376206161 1989. Theoretical Biology: Epigenetic and Evolutionary Order for Complex Syste...

MetrolinkInfoPemilikTransport for Greater ManchesterWilayahManchester RayaJenisTrem/kereta api ringan[1]Jumlah jalur 5 (2 sedang dibangun) Bury Line Altrincham Line Eccles Line South Manchester Line Oldham and Rochdale Line East Manchester Line (sedang dibangun) Manchester Airport Line (sedang dibangun) Trafford Line (planned)[2] Jumlah stasiun50 (Juni 2012, setidaknya 105 pada 2016)Penumpang harian54.000 (2009/10)Kantor pusatMetrolink House, Queens Road, Manchester, InggrisOp...

Chrome Web StoreTanggal diluncurkanDesember 2010; Galat: first parameter cannot be parsed as a date or time. (2010-12)Situs webchrome.google.com/webstore Toko Web Chrome (bahasa Inggris: Chrome Web Store) adalah toko daring Google untuk peramban web Chrome. Pada 2019, Toko Web Chrome menampung sekitar 190.000 ekstensi dan aplikasi web.[1] Sejarah Toko Web Chrome diresmikan pada bulan Desember 2010,[2] dan dibuka pada tanggal 11 Februari 2011, dengan merilis Google Chrome ...

Germanic duke of Italy (c. 433 – 493) OdoacerRex/DuxPatriciusCoin of Odoacer minted in Ravenna, 477, with Odoacer in profile, depicted with a barbarian moustacheKing of ItalyReign4 September 476 – 15 March 493SuccessorTheodoric the GreatBornc. 433[1]Died15 March 493 (aged about 60)Ravenna, Kingdom of ItalySpouseSunigildaIssueThelaFatherEdekoReligionArianism Odoacer[a] (/ˌoʊdoʊˈeɪsər/ OH-doh-AY-sər;[b] c. 433 – 15 March 493 AD), also spelled Odo...

Government department that ran South Australia's railways from 1854 to 1978 Not to be confused with South Australian Railway Company. South Australian RailwaysIndustryRailway operatorFounded1854Defunct28 February 1978FateSold to the federal governmentSuccessorAustralian NationalHeadquartersAdelaide, AustraliaArea servedSouth AustraliaParentGovernment of South Australia South Australian Railways (SAR) was the statutory corporation through which the Government of South Australia built and opera...

2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl（英文）（波兰文）2020年夏季奥林匹克运动会（東京）2021年7月23日至8月8日（受2019冠状病毒病疫情影响推迟，但仍保留原定名称）運動員206參賽項目24个大项旗手开幕式：帕维尔·科热尼奥夫斯基（游泳）和马娅·沃什乔夫斯卡（自行车）[1]闭幕式：卡罗利娜·纳亚（皮划艇）&#...

Untuk generasi pertama dan kedua Toyota Voxy, lihat Toyota NAV1. Toyota Voxy2022 Toyota Voxy (MZRA90W, Indonesia)InformasiProdusenToyotaJuga disebutToyota NoahToyota Esquire (2014–2021)[1]Toyota NAV1 (Indonesia, 2012–2017)Masa produksiNovember 2001[2] – sekarangBodi & rangkaKelasMPV ukuran menengahBentuk kerangkaMPV 5 pintuTata letakMesin depan, penggerak roda depan / penggerak 4 rodaMobil terkaitToyota Kijang InnovaKronologiPendahuluToyota TownAce/LiteAce ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Bagian dari seri tentang PemerintahanKeuangan publik KebijakanKebijakan ekonomiKebijakan fiskal · Kebijakan moneterKebijakan perdagangan · Kebijakan investasiKebijakan pertanian · Kebijakan industriKebijakan energi ...

نادي الشرق بالدلم شعار نادي الشرق الاسم الكامل نادي الشرق تأسس عام 1962 الملعب اسم الملعب الدلم، السعودية(السعة: 0,000) البلد السعودية[1]  الدوري دوري الدرجة الثالثة السعودي 2023/2024 ( صعد لدوري الدرجة الثانية ) ---- الإدارة المالك وزارة الرياضة الرئيس الأستاذ داود بن محمد الم�...

Stimulus package American Recovery and Reinvestment Act of 2009Long titleAn Act making supplemental appropriations for job preservation and creation, infrastructure investment, energy efficiency and science, assistance to the unemployed, State, and local fiscal stabilization, for the fiscal year ending September 30, 2009, and for other purposes.Acronyms (colloquial)ARRANicknamesRecovery ActEnacted bythe 111th United States CongressEffectiveFebruary 17, 2009CitationsPublic law111-5Statute...

In this Spanish name, the first or paternal surname is Sánchez and the second or maternal family name is Reyes. Mexican sports journalist and model Jimena SánchezSánchez in 2018BornJimena Sánchez Mejía Reyes (1984-09-28) September 28, 1984 (age 39)Mexico City, MexicoOccupationsSports journalisttelevision hostmodelactressYears active2008 - presentTelevisionLo Mejor de Fox SportsMLB en FOXWWE Saturday NightSpouse Tis Zombie ​(m. 2021)​Modelin...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menamba...

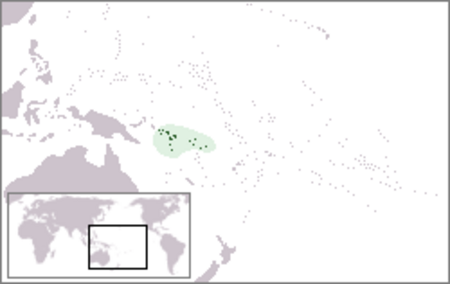
المقالة الرئيسة: أيزو 3166-2 أيزو 31166-2:SB هو الجزء المخصص لدولة جزر سليمان في أيزو 3166-2، وهو جزء من معيار أيزو 3166 الذي نشرته المنظمة الدولية للتوحيد القياسي (أيزو)، والذي يُعرف رموز لأسماء التقسيمات الرئيسية (مثل الأقاليم، الجهات، المقاطعات أو الولايات) من جميع البلدان في ترميز ...

Iranian singer (born 1987) SevdalizaSevdaliza performing in 2018Background informationBirth nameSevda AlizadehBorn (1987-09-01) 1 September 1987 (age 37)Tehran, IranOriginRotterdam, NetherlandsGenresElectronicalternative R&Btrip hopavant-popOccupation(s)SingersongwriterproducerYears active2014–presentLabelsTwisted EleganceWebsitesevdaliza.comMusical artist Sevda Alizadeh (Persian: سِودا علیزاده; born 1 September 1987), known professionally as Sevdaliza, is an Iranian-Du...

Civil Rights ActStatoStati Uniti d'America Tipo leggelegge federale Promulgazione1866 Il Civil Rights Act del 1866 è una legge federale degli Stati Uniti d'America che dichiara che chiunque nato negli Stati Uniti e non soggetto ad alcuna nazione straniera è un cittadino statunitense senza riguardo alla sua razza, colore, precedente condizione di schiavitù o servitù involontaria. È la legge con la quale, dopo la guerra di secessione, fu abolita la schiavitù negli stati confederati e quin...

Schematic picture of a 2-bridge knot. Bridge number 231516371... In the mathematical field of knot theory, a 2-bridge knot is a knot which can be regular isotoped so that the natural height function given by the z-coordinate has only two maxima and two minima as critical points. Equivalently, these are the knots with bridge number 2, the smallest possible bridge number for a nontrivial knot. Other names for 2-bridge knots are rational knots, 4-plats, and Viergeflechte (German for 'four br...