Diracin deltafunktio
|
Read other articles:

Tim Hortons Inc. (The TDL Group Corp.)JenisPerusahaan publikKode emitenTSX: THINYSE: THIIndustriRestoran[1]DidirikanHamilton, Ontario (1964)KantorpusatOakville, OntarioCabang4.000+Wilayah operasi KanadaTemplat:IRE Uni Emirat Arab Britania Raya Amerika SerikatTokohkunciPaul D. House, (Ketua Eksekutif, CEO sementara), Don Schroeder, CEO, dan Presiden, dan Direktur (1 Maret 2008 – 26 Mei 2011)Tim Horton dan Ron Joyce, pendiriPendapatan CA$2,536 milyar (201...

Australian Astronomical Observatory telescope Anglo-Australian TelescopePart ofAustralian Astronomical ObservatorySiding Spring Observatory Location(s)New South Wales, AUSCoordinates31°16′31″S 149°04′01″E / 31.2754°S 149.067°E / -31.2754; 149.067 OrganizationAustralian Astronomical Observatory Altitude1,100 m (3,600 ft) Built–1974 (–1974) First light27 April 1974 Telescope styleCassegrain reflectoroptical telescop...

American politician Ebenezer Jenckes PennimanMember of the U.S. House of Representativesfrom Michigan's 1st districtIn officeMarch 4, 1851 – March 3, 1853Preceded byAlexander W. BuelSucceeded byDavid Stuart Personal detailsBorn(1804-01-11)January 11, 1804Lansingburgh, New York, U.S.DiedApril 12, 1890(1890-04-12) (aged 86)Plymouth, Michigan, U.S.Resting placeRiverside CemeteryPlymouth, MichiganCitizenshipUSPolitical partyWhigSpouse(s)Maryette PennimanEliza Connor Pe...

Pseudoscientific attempts to change sexuality or gender identity Conversion therapyClaimsOne's sexual orientation, romantic orientation, gender identity, or gender expression can be changed to fit heterosexual, heteroromantic, and cisgender norms.Notable proponentsEx-gay movement(Overview of pseudoscientific concepts) Part of a series onLGBT rights Lesbian ∙ Gay ∙ Bisexual ∙ Transgender Overview Rights Movements Student Germany (pre-1933) United States Intersex rights Social attitudes T...

Bandar Udara Internasional Port HedlandPintu masuk terminal, 2012.IATA: PHEICAO: YPPDInformasiJenisUmumPemilikTown of Port HedlandPengelolaManager Airport, Port Hedland International AirportMelayaniPort Hedland and South HedlandLokasiPort Hedland, Australia BaratKetinggian dpl mdplSitus webporthedlandairport.com.auPetaYPPDLokasi di Australia BaratLandasan pacu Arah Panjang Permukaan m kaki 14/32 2,500 8.202 Chipseal 18/36 1,000 3.281 Chipseal Statistik (2010/11)Penumpang367.690Perge...
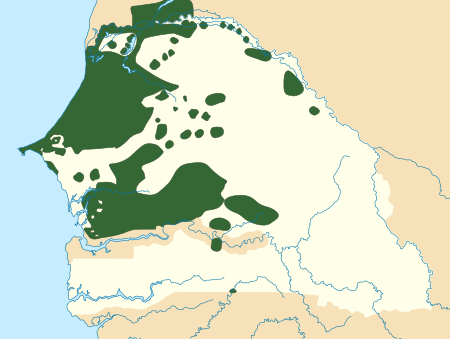
WolofWolofParlato in Senegal Gambia Guinea Guinea-Bissau Mali Mauritania LocutoriTotale12,3 milioni (Ethnologue, 2022) ClassificaNon nelle prime 100 (hanno almeno 5,5 milioni di parlanti L1) Altre informazioniTipoSVO TassonomiaFilogenesiLingue niger-kordofaniane Lingue congo-atlantiche Lingue atlantiche Lingue atlantiche settentrionali Lingue senegambiane Lingue fula-wolof &...

KolonelAssimi Goïta Presiden MaliSementaraPetahanaMulai menjabat 26 Mei 2021Perdana MenteriLowongPendahuluBah Ndaw (presiden sementara)PenggantiPetahanaWakil Presiden MaliMasa jabatan25 September 2020 – 25 Mei 2021PresidenBah NdawPendahuluMalick DiawPenggantiLowongKetua Komite Nasional untuk Keselamatan RakyatMasa jabatan19 Agustus 2020 – 25 September 2020Perdana MenteriKosongPendahuluIbrahim Boubacar Keïta (Presiden)PenggantiBah Ndaw (Presiden) Informasi pribadiLa...

Airport serving West Yorkshire, England Not to be confused with Leeds East Airport. Leeds Bradford AirportIATA: LBAICAO: EGNMSummaryAirport typePublicOwnerAMP CapitalOperatorLeeds Bradford Airport LimitedServesWest YorkshireNorth YorkshireLocationYeadon, England, United KingdomOpened17 October 1931; 92 years ago (1931-10-17)Operating base forJet2.comRyanairElevation AMSL681 ft / 208 mCoordinates53°51′58″N 001°39′39″W / 53.86611°N 1.6...

Origin, history and development of conservatism in Turkey Part of a series onConservatism Variants Authoritarian Corporatist Cultural Fiscal Green Liberal Libertarian Moderate National Paternalistic Populist Pragmatic Progressive Reactionary Religious Social Traditionalist Ultra Principles Ancestral worship Authority Traditional Class collaboration Collective identity Cultural heritage Cultural values Culture of life Pro-Life Discipline Duty Elitism Aristocracy Meritocracy Noblesse oblige Eth...

39°44′25″N 104°58′29″W / 39.74028°N 104.97472°W / 39.74028; -104.97472 Ogden TheatreFormer namesFox Theatres, National General Cinemas (NGC), Mann Theatres and Landmark Theater (1977-90)Address935 E Colfax AveDenver, CO 80218-1914LocationCapitol HillOwnerDoug KauffmanOperatorAEG Rocky MountainsCapacity1,600Current usemusic venueConstructionBroke groundNovember 13, 1916; 107 years ago (1916-11-13)OpenedSeptember 6, 1917; 106 ye...

STXBP5 المعرفات الأسماء المستعارة STXBP5, Tomosyn, LGL3, LLGL3, Nbla04300, syntaxin binding protein 5 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 604586 MGI: MGI:1926058 HomoloGene: 16402 GeneCards: 134957 علم الوجود الجيني الوظيفة الجزيئية • GO:0005097، GO:0005099، GO:0005100 GTPase activator activity• syntaxin-1 binding• syntaxin binding• myosin II binding المك�...

Oliver Makor Informasi pribadiNama lengkap Oliver Paul MakorTanggal lahir 9 Oktober 1973 (umur 50)Tempat lahir Monrovia, LiberiaTinggi 168 m (551 ft 2 in)Posisi bermain Gelandang tengahInformasi klubKlub saat ini Persik KediriNomor 11Karier senior*Tahun Tim Tampil (Gol) 1991–1992 1993 1994 1994–1996 1996–1997 1997–1999 1999–2001 2001–2002 2002–2009 2010–2011 2012-kini Black Star Julius Berger FC Canon Yaoundé Grenoble Foot 38 Tours FC Limoges FC Proodefti...

Due notti con CleopatraLingua originaleitaliano Paese di produzioneItalia Anno1954 Durata78 min Generecomico RegiaMario Mattoli SoggettoEttore Scola, Ruggero Maccari SceneggiaturaRuggero Maccari, Ettore Scola Casa di produzioneExcelsa, Rosa Film Distribuzione in italianoMinerva Film FotografiaKarl Struss, Riccardo Pallottini MontaggioRoberto Cinquini MusicheArmando Trovajoli ScenografiaAlberto Boccianti CostumiGaia Romanini Interpreti e personaggi Alberto Sordi: Cesarino Sophia Loren: Cleopat...

لمعانٍ أخرى، طالع درايدن (توضيح). درايدن الإحداثيات 49°46′48″N 92°50′02″W / 49.78°N 92.833888888889°W / 49.78; -92.833888888889 [1] [2] تاريخ التأسيس 1895 تقسيم إداري البلد كندا[3][4] خصائص جغرافية ارتفاع 371.90 متر عدد السكان عدد السكان 7749 (2016)[5...

Malaysian/Singaporean breakfast item Kaya toastKaya toastAlternative namesRoti bakarTypeToastCourseBreakfastPlace of originStraits Settlements (present day Malaysia and Singapore)[1][2]Region or stateSoutheast AsiaCreated byHainanese cooks during the Straits Settlements periodServing temperatureHotMain ingredientskaya (coconut jam)Glycemic index 49 (low) Media: Kaya toast Kaya toast is a dish consisting of two slices of toast with butter and kaya (coconut jam),...

Academic journalFeminist TheologyDisciplineTheologyLanguageEnglishEdited byLisa Isherwood, Lillalou Hughes, Beverley ClackPublication detailsHistory1992 -presentPublisherSAGE PublicationsFrequencyTri-annuallyImpact factor(2010)Standard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )ISO 4Fem. Theol.IndexingCODEN (alt · alt2) · JSTOR (alt) · LCCN (alt)MIAR · NLM ...

OmišMunicipality and townOmiš dari udaraKoordinat: 43°26′N 16°41′E / 43.433°N 16.683°E / 43.433; 16.683Negara KroasiaKabupaten Split-DalmasiaPemerintahan • WalikotaIvan Kovačić (Most)Luas • Total266 km2 (103 sq mi)Populasi (2011) • Total14,936Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST) 43°26′N 16°41′E / 43.433°N 16.683°E / 43.433; 16.683 Omiš ...

日本ローカルの事柄については「2007年の日本」をご覧ください。 千年紀: 3千年紀世紀: 20世紀 - 21世紀 - 22世紀十年紀: 1980年代 1990年代 2000年代 2010年代 2020年代年: 2004年 2005年 2006年 2007年 2008年 2009年 2010年 2007年 2007年の話題 主権国家 - 周年 - 表彰 指導者 国の指導者 - 宗教指導者 - 国際機関の指導者 社会 政治 - �...

Ini adalah nama Tionghoa; marganya adalah Chua (蔡). Yang Berhormat TuanChua Tian ChangMP蔡添强 Anggota Parlemen Malaysiadapil Batu, Kuala LumpurPetahanaMulai menjabat 8 Maret 2008PendahuluNg Lip YongPenggantiPetahanaMayoritas9,455Wakil Presiden Parti Keadilan RakyatPetahanaMulai menjabat 2008Ketua Informasi Parti Keadilan RakyatMasa jabatan2004–2008PenggantiMuhammad Nur Manuty Informasi pribadiLahir21 Desember 1963 (umur 60)Melaka, MalaysiaPartai politikPKR – Pakatan Rak...

Unclear ethnic group from North Europe, described by Tacitus The Aesti were located around the Baltic Sea. The Aesti (also Aestii, Astui or Aests) were an ancient people first described by the Roman historian Tacitus in his treatise Germania (circa 98 AD).[1] According to Tacitus, the territory of Aesti was located somewhere east of the Suiones (Swedes). Overview According to Tacitus, the Aesti live Upon the right of the Suevian Sea [2] and have the same customs and attire as ...













![{\displaystyle \delta (x^{2}-\alpha ^{2})={\frac {1}{2|\alpha |}}[\delta (x+\alpha )+\delta (x-\alpha )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/844d1dbe284e11c90c73bf79eed231f528435310)






