Órbita elíptica

En el dibujo, un cuerpo orbita alrededor de otro más grande (como un planeta alrededor del Sol) describiendo una órbita elíptica. El mayor estará localizado en uno de los focos de la elipse.

Se denomina órbita elíptica a aquella órbita de un astro girando en torno a otro describiendo una elipse. El astro central se sitúa en uno de los focos de la elipse. En astrodinámica o mecánica celeste y geometría una órbita elíptica tiene una excentricidad mayor que cero y menor que uno (si posee excentricidad 1 es una órbita circular y con excentricidad 2 es una órbita parabólica). La energía específica de una órbita elíptica es negativa. Ejemplos de órbitas elípticas incluyen: Órbita de transferencia Hohmann (ejecutada cuando un satélite cambia la cota de giro orbital), órbita Molniya y la órbita tundra.

Puntos notables de una trayectoria elíptica

Los puntos notables son aquellos que se describen como únicos y característicos de la trayectoria; de esta forma se tiene:

  • Periapsis, o lugar más cercano de la trayectoria al cuerpo central (en el caso de la Tierra, se denomina perigeo, y respecto al Sol se denomina también perihelio).
  • Apoapsis, o al contrario que el periapsis, es el lugar más alejado de la trayectoria (se denomina también apogeo en el caso de la Tierra y afelio en el caso del Sol).

Velocidad

Bajo las suposiciones estándar en astrodinámica la velocidad orbital () de un cuerpo que describe una trayectoria sobre una órbita elíptica se puede calcular como:

Donde:

  • es un parámetro gravitacional estándar,
  • es la distancia radial desde el cuerpo orbitante al cuerpo central,
  • es la longitud del semi-eje mayor de la elipse.

Conclusiones:

  • La velocidad no depende de la excentricidad pero se puede determinar por la longitud del semi-eje mayor (),
  • La ecuación de la velocidad es muy similar a la obtenida en las trayectorias hiperbólicas, con la diferencia de que la expresión para es positiva.

Periodo orbital

Bajo las suposiciones estándar en astrodinámica el periodo orbital () de un cuerpo que viaja sobre una trayectoria elíptica puede ser calculado mediante la siguiente fórmula:

Donde:

Conclusiones:

  • El periodo orbital es igual que el de un cuerpo que viaja en una órbita circular con radio igual al semi-eje mayor de la elipse ().
  • El periodo orbital no depende de la excentricidad (Véase la tercera Ley de Kepler).

Energía

Bajo las suposiciones estándar en astrodinámica la energía específica orbital () de un cuerpo que se mueve en una órbita elíptica es negativa y la ecuación de conservación de energía orbital para esta órbita toma la forma de:

Donde:

  • es la velocidad orbital del cuerpo que orbita,
  • es la distancia radial entre el cuerpo orbitante y el cuerpo central,
  • es la longitud del semi-eje mayor de la elipse,

Conclusiones:

  • La energía específica orbital para un movimiento elíptico es independiente de la excentricidad y está determinado solo por el semi-eje mayor de la elipse.

Usando el teorema de virial encontramos que:

  • El tiempo medio de la energía potencial específica es igual a 2ε
  • El tiempo medio de r-1 es a-1
  • El tiempo medio de la energía cinética específica es igual a -ε.

Véase también

Enlaces externos

Read other articles:

Asam glukuronat

Asam glukuronat Nama Nama IUPAC (2S,3S,4S,5R,6R)-3,4,5,6-Tetrahydroxyoxane-2-carboxylic acid Nama lain β-D-glucopyranuronic acid Penanda Nomor CAS 6556-12-3 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChemSpider 392615 Y Nomor EC MeSH Glucuronic+acid PubChem CID 441478 Nomor RTECS {{{value}}} UNII 8A5D83Q4RW Y CompTox Dashboard (EPA) DTXSID40273973 InChI InChI=1S/C6H10O7/c7-1-2(8)4(5(10)11)13-6(12)3(1)9/h1-4,6-9,12H,(H,10,11)/t1-,2-,3+,4-,6-/m0/s1 YKey: A...

 

Atletik pada Pekan Olahraga Nasional 2016 – 4 × 400 meter estafet putri

Atletik padaPekan Olahraga Nasional 2016 Lintasan 100 m putra putri 200 m putra putri 400 m putra putri 800 m putra putri 1500 m putra putri 5000 m putra putri 10.000 m putra putri 100 m gawang putri 110 m gawang putra 400 m gawang putra putri 3000 m h'rintang putra putri 10.000 m jalan cepat putra 4×100 m estafet putra putri 4×400 m estafet putra putri Jalan raya Maraton putra putri 20 km jalan cepat putra putri Lapangan Lompat tinggi putra putri Lompat galah putra putri Lompat jauh putra...

 

Article 59 de la Constitution de la Cinquième République française

Cet article est une ébauche concernant le droit français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Article 59 de la Constitution du 4 octobre 1958 Données clés Présentation Pays France Langue(s) officielle(s) Français Type Article de la Constitution Adoption et entrée en vigueur Législature IIIe législature de la Quatrième République française Gouvernement Charles de Gaulle (3e) Promulgation 4...

Pangkalan Udara TNI Angkatan Udara Atang Sendjaja

Pangkalan Udara TNI AU Atang SendjajaLambang LanudNegara IndonesiaCabang TNI Angkatan UdaraTipe unitLanud Tipe APeranPangkalan Angkatan UdaraBagian dariKomando Operasi Udara ILanudAtang Senjaya, Kemang, BogorPelindungTentara Nasional IndonesiaMotoPrayatna Kerta GeganaSitus webwww.tni-au.mil.id Pangkalan Udara Atang SenjayaAtang Senjaya AirbaseIATA: -ICAO: WIHJInformasiJenisMiliterPengelolaTNI Angkatan UdaraLokasiKemang, Kabupaten Bogor, Jawa Barat, IndonesiaKetinggian dpl164 mdplKoo...

 

Arteri vertebralis

Arteri di daerah leher. Arteri vertebralis berjalan dari arteri subklavia dan bergabung untuk membentuk arteri basilaris. Arteri vertebralis merupakan sepasang arteri besar di daerah leher.[1] Arteri ini memiliki empat segmen yaitu segmen preforaminal, segmen foraminal, segmen eksradural, dan segmen intradural.[2] Pada segmen preforaminal, arteri vertebralis berasal dari bagian pertama arteri subklavia dan berjalan secara posterosuperior melewati otot skalenus anterior dan lon...

 

San Benigno Canavese

San Benigno Canavesecomune San Benigno Canavese – VedutaUno scorcio del centro storico LocalizzazioneStato Italia Regione Piemonte Città metropolitana Torino AmministrazioneSindacoAlberto Graffino (lista civica) dal 13-6-2022 TerritorioCoordinate45°13′37.39″N 7°47′06.08″E / 45.227052°N 7.785021°E45.227052; 7.785021 (San Benigno Canavese)Coordinate: 45°13′37.39″N 7°47′06.08″E / 45.227052°N 7.785021°E45.22705...

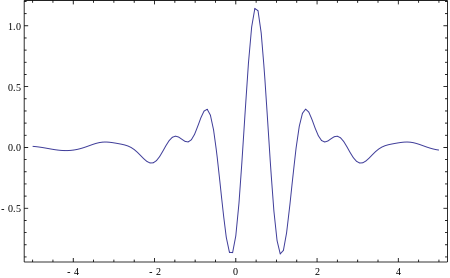
Wavelet

Function for integral Fourier-like transform For the concept in physics, see Wave packet. A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a brief oscillation. A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. Seismic wavelet For example, a wavelet...

 

Rick Tyler

American pastor (born 1957) For the DC Comics character, see Hourman (Rick Tyler). Rick TylerRichard Tyler Jr., July 7, 2020 mug shotBornRichard Seburn Tyler, Jr. (1957-10-10) October 10, 1957 (age 66)Miami, Florida, United StatesNationalityAmericanKnown forwhite nationalismPolitical partyIndependent (before 2019)American Freedom Party (2019 - present) Richard Seburn Tyler Jr.[1] (born October 10, 1957) is an American pastor and far-right political candidate from Tennessee. ...

 

Takuya Miyamoto (1983)

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Takuya MiyamotoInformasi pribadiNama lengkap Takuya MiyamotoTanggal lahir 8 Juli 1983 (umur 40)Tempat lahir Prefektur Hiroshima, JepangPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2006-2007 Cerezo Osaka 2008-2012 Montedio Yamagata 2013 Avis...

Surat Neacşu

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Surat Neacşu – berita · surat kabar · buku · cendekiawan · JSTORSurat Neacşu Surat Neacşu dari Câmpulung, ditulis pada 1521, adalah dokumen tertua dalam bahasa Rumania lama. Ditulis dengan menggunaka...

 

Nelson Figueroa

American baseball player (born 1974) Baseball player Nelson FigueroaFigueroa with the Uni-Lions in 2014PitcherBorn: (1974-05-18) May 18, 1974 (age 50)Brooklyn, New York, U.S.Batted: SwitchThrew: RightProfessional debutMLB: June 3, 2000, for the Arizona DiamondbacksCPBL: September 15, 2007, for the Uni-President LionsLast appearanceMLB: May 9, 2011, for the Houston AstrosCPBL: August 28, 2014, for the Uni-President 7-Eleven Lions...

 

2019 CAFA U-23 Women's Championship

2019 CAFA U-23 Women's ChampionshipЧемпионат CAFA-2019 среди женских олимпийских сборныхTournament detailsHost country TajikistanDates22–28 NovemberTeams6 (from 1 sub-confederation)Venue(s)2 (in 2 host cities)Final positionsChampions Uzbekistan (1st title)Runners-up IranThird place TajikistanFourth place KyrgyzstanTournament statisticsMatches played15Goals scored67 (4.47 per match)Attendance945 (63 per ...

Nakhon Phanom

For other uses, see Nakhon Phanom (disambiguation). Town in Nakhon Phanom Province, ThailandNakhon Phanom นครพนมTownWat Phra That PhanomNakhon PhanomCoordinates: 17°24′25″N 104°46′51″E / 17.40694°N 104.78083°E / 17.40694; 104.78083Country ThailandProvincesNakhon Phanom ProvinceAmphoeMueang Nakhon Phanom DistrictElevation149 m (489 ft)Population (2006)27,591Time zoneUTC+7 (ICT)ClimateAw Nakhon Phanom (Thai: นครพนม,...

 

Governor-General of Australia

Representative of the monarch of Australia For a list of office holders, see List of governors-general of Australia. Governor-General of the Commonwealth of AustraliaBadgeFlag of the governor-generalIncumbentDavid Hurleysince 1 July 2019ViceregalStyleHis Excellency the HonourableResidenceGovernment House (Canberra)Admiralty House (Sydney)AppointerMonarch of Australiaon the advice of the prime ministerTerm lengthAt His Majesty's pleasure(typically 5 years)[1]Formation29 October 19...

 

Metaheuristik

Dalam bidang Ilmu Komputer dan Optimasi Matematika, metaheuristik (bahasa Inggris: metaheuristic) didefinisikan sebagai suatu prosedur tingkat tinggi atau pendekatan heuristik yang dirancang agar dapat menemukan, menghasilkan, mengoptimalkan, atau memilih suatu heuristik (algoritma pencarian parsial) yang dapat memberikan solusi yang memadai terhadap suatu permasalahan optimasi atau pemelajaran mesin. Secara khusus, metaheuristik digunakan pada permasalahan yang memiliki keterbatasan informas...

United States Court of Appeals for the Seventh Circuit

Current United States federal appellate court United States Court of Appeals for the Seventh Circuit(7th Cir.)LocationEverett McKinley Dirksen U.S. Courthouse(Chicago)Appeals fromCentral District of IllinoisNorthern District of IllinoisSouthern District of IllinoisNorthern District of IndianaSouthern District of IndianaEastern District of WisconsinWestern District of WisconsinEstablishedJune 16, 1891Judges11Circuit JusticeAmy Coney BarrettChief JudgeDiane S. Sykeswww.ca7.uscour...

 

Columbinus

Part of a series of articles on theColumbine High School massacre Location:Columbine High School(Columbine, Colorado) Perpetrators:Eric Harris and Dylan Klebold Victims Cassie Bernall Austin Eubanks Rachel Scott Weaponry Intratec TEC-9 Mini Hi-Point 995 Carbine Savage 67H pump-action shotgun Stevens 311D double barreled sawed-off shotgun Related persons Dave Cullen Sue Klebold Danny Ledonne Sol Pais Bill White Media A Mother's Reckoning (2016) April Showers (2009) Bowling for Columbine (2002)...

 

Naomie Harris

Naomie HarrisNaomie Harris saat penayangan perdana film Skyfall di Sydney pada 16 November 2012.LahirNaomie Melanie Harris6 September 1976 (umur 47) LondonAlmamaterUniversitas CambridgePekerjaanAktrisTahun aktif1987–sekarang Naomie Melanie Harris (lahir 6 September 1976) adalah seorang aktris berkebangsaan Inggris yang mulai terkenal saat berperan sebagai Selena di film 28 Days Later. Ia dilahirkan di London. Dia berkarier di dunia film sejak tahun 1987. Filmografi Film Televisi ...

محافظة ثار

  هذه المقالة عن محافظة ثار. لمدينة ثار، طالع ثار. محافظة ثار ثار محافظة علم محافظة ثارعلمOfficial seal of محافظة ثارشعار الاسم الرسمي محافظة ثار  صورة لخريطة محافظة ثار نسبةً لمنطقة نجرانموقع محافظة ثار نسبةً لمنطقة نجران صورة لخريطة محافظة ثار والمحافظات الأخرى في منطقة...

 

Phloeostichidae

Family of beetles PhloeostichidaeTemporal range: Cenomanian–Recent PreꞒ Ꞓ O S D C P T J K Pg N Phloeostichus denticollis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Coleoptera Suborder: Polyphaga Infraorder: Cucujiformia Superfamily: Cucujoidea Family: PhloeostichidaeReitter, 1911 Genera See text Phloeostichidae is a family of beetles in the superfamily Cucujoidea. They are typically found under the bark of dead trees. Larvae ha...