Topología cociente
|
Read other articles:

Christopher A. SimsLahir21 Oktober 1942 (umur 81)Washington, D.C.KebangsaanAmerikaInstitusiPrinceton UniversityBidangMacroeconomicsEconometricsTime seriesAlma materHarvard University, (A.B, PhD)UC Berkeley[1]KontribusiUse of vector autoregressionPenghargaanNobel Ekonomi (2011)Informasi di IDEAS / RePEc Christopher Albert Chris Sims (lahir 21 Oktober 1942) adalah seorang ahli ekonometrika dan ekonomi makro. econometrician and macroeconomist. Saat ini ia menjadi pro...

Artikel ini bukan mengenai Supremasi kepausan, Keutamaan Petrus, Papisme, atau Hierokrasi. Paus Bonifasius VIII bersama dewan kardinal, ilustrasi dekretale (Kumpulan Surat Keputusan Paus) dari abad ke-14 Primasi, Supremasi, dan Infalibilitas Paus Selayang Pandang Primasi Petrus & Primasi Paus Supremasi Paus Infalibilitas Paus Konsili Vatikan I § Infalibilitas Paus BatrikDibanding Paus Primasi Paus Takhta Keuskupan § Gereja Katolik Apiarius orang Sika § Naik Banding ke Uskup Roma Pentar...

Nahuel Guzmán UANL Tigres 2015Informasi pribadiNama lengkap Nahuel Ignacio Guzmán[1]Tanggal lahir 10 Februari 1986 (umur 38)Tempat lahir Santa Fe,ArgentinaTinggi 192 cm (6 ft 4 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Tigres UANLNomor 1Karier junior Newell's Old BoysKarier senior*Tahun Tim Tampil (Gol)2005–2014 Newell's Old Boys 81 (0)2008–2009 → CSIR (pinjaman) 30 (0)2014– Tigres UANL 158 (0)Tim nasional2014– Argentina 6 (0) * Penam...

Lembah Hunza pada musim gugur akhir. Lembah Hunza pada musim semi awal. Hunza (Burushaski dan bahasa Urdu: ہنزہ) adalah lembah bergunung yang terletak di region Gilgit–Baltistan di Pakistan. Lembah ini terletak di ujung utara Pakistan. Bahasa-bahasa yang dituturkan di wilayah ini meliputi Burushaski, Wakhi dan Shina. Tingkat melek huruf di lembah Hunza diyakini melebihi 95%.[1] Setiap anak telah terdidik hingga paling tidak tingkatan sekolah menengah atas.[1] Sebagia...

Pancreatic polypeptide cells (PP cells), or formerly as gamma cells (γ-cells), or F cells, are cells in the pancreatic islets (Islets of Langerhans) of the pancreas. Their main role is to help synthesize and regulate the release of pancreatic polypeptide (PP), after which they have been named. The pancreatic islets, where PP cells reside, was discovered in 1869 by a German pathological anatomist and scientist, Paul Langerhans. PP cells help to make up the pancreas but are smallest in proport...

American historian (1918–1999) George Lachmann MosseGeorge Mosse at Pembroke College, Cambridge University, 1991BornGerhard Lachmann Mosse(1918-09-20)September 20, 1918Berlin, Kingdom of Prussia, German EmpireDiedJanuary 22, 1999(1999-01-22) (aged 80)Madison, Wisconsin, U.S.Board member ofCo-editor, Journal of Contemporary HistoryAwardsGoethe Medal (1988) Leo Baeck Medal (1998)Academic backgroundEducationSchule Schloss Salem, Cambridge UniversityAlma materHaverford CollegeHarvard ...

Not to be confused with Ostoja of Bosnia. Original Ostoja coat of arms The Clan of Ostoja (old Polish: Ostoya) was a powerful group of knights and lords in late-medieval Europe. The clan encompassed families in the Polish–Lithuanian Commonwealth (including present-day Belarus and Ukraine), Hungary and Upper Hungary (now Slovakia), Transylvania, and Prussia. The clan crest is the Ostoja coat of arms,[1][2] and the battle cry is Ostoja (Mainstay) or Hostoja (Prevail). The clan...

Voce principale: Real Zaragoza. Real ZaragozaStagione 2009-2010Sport calcio Squadra Real Saragozza Allenatore Marcelino García Toral (fino al 12/12/2009) José Aurelio Gay (dal 12/11/2010[1]) All. in seconda Rubén Uría (fino al 12/12/2009) Nayim (dal 12/12/2009) Presidente Eduardo Bandrés Moliné(fino al 30/12/2009) Agapito Iglesias (dal 30/12/2009) Primera División14º posto Coppa del ReSedicesimi di finale Maggiori presenzeCampionato: Leonardo Ponzio (34)Totale: Leonardo ...

此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Louis-Marie de La Révellière-LépeauxPotret karya Gerard van Spaendonck pada sekitar tahun 1797 Informasi pribadiLahir(1753-08-24)24 Agustus 1753Montaigu, VendéeMeninggal24 Maret 1824(1824-03-24) (umur 70)MakamPemakaman Père LachaiseKebangsaanPrancisPekerjaanPengacaraDikenal karenaKonvensi Nasional; Direktori PrancisSunting kotak info • L • B Louis Marie de La Révellière-Lépeaux (24 Agustus 1753 – 24 Maret 1824) adalah seorang deputi untuk Konvensi Na...

Code reference for the US Army Air Forces' role in the Manhattan Project This article is about the Manhattan Project operation. For the method of adding a thin layer of silver to an object, see Silver plate. Bockscar, a Silverplate B-29 Superfortress of the 509th Composite Group, dropped an atomic bomb on Nagasaki Silverplate was the code reference for the United States Army Air Forces' participation in the Manhattan Project during World War II. Originally the name for the aircraft modificati...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Bridge in Washington, D.C., U.S. Kutz Memorial BridgeCoordinates38°53′N 77°02′W / 38.89°N 77.04°W / 38.89; -77.04CarriesIndependence AvenueCrossesTidal BasinLocaleWashington, D.C., United StatesNamed forCharles W. KutzHistoryArchitectPaul Philippe CretConstructed byAlexander & Repass CompanyConstruction end1943Location The Kutz Memorial Bridge is a bridge that carries Independence Avenue across the Tidal Basin in Washington, D.C., in the United States. Arch...

Location of Washington County in New York Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) List of the National Register of Historic Places listings in Washington County, New York This is intended to be a complete list of properties and districts listed on the National Register of Historic Places in Washington County, New York. The locations of National Register properties and districts (at least ...

For the mountain range in Lehigh Valley region of Pennsylvania, see South Mountain (Eastern Pennsylvania). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: South Mountain Maryland and Pennsylvania – news · newspapers · books · scholar · JSTOR (September 2011) (Learn how and when to remove this message) M...

Questa voce sull'argomento società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Saint-Vincent ChâtillonCalcio Segni distintiviUniformi di gara Casa Trasferta Colori sociali Azzurro, granata Dati societariCittàSaint-Vincent Châtillon Nazione Italia ConfederazioneUEFA Federazione FIGC CampionatoPrima Categoria Fondazione1909 Rifondazione2013Presidente Monica Pisoni Allenatore Dominique Grenier[1] StadioStadio Pie...

Cet article est une ébauche concernant une localité anglaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Thorpe. ThorpeGéographiePays Royaume-UniRégion Yorkshire-et-HumberRégion Angleterre du Nord-EstComté cérémonial Yorkshire du NordRégion du conseil Yorkshire du NordDistrict non métropolitain CravenCoordonnées 54° 03′ 08″ N, 1° 5...

Irish and British peer (1945–2019) Shaun James Christian Welbore Ellis Agar, 6th Earl of Normanton (21 August 1945 – 13 February 2019) was an Irish and British peer, soldier, landowner, and powerboat racer. From birth until 1967 he was known by the courtesy title of Viscount Somerton. As Baron Somerton of Somerley and later as Baron Mendip he was a member of the House of Lords from 1967 until the reform of the Lords in 1999. Early life Normanton was the elder son of Edward John Sidney Chr...

Iraqi Shi'a paramilitary group Asa'ib Ahl al-Haq عصائب أهل الحقLeaderQais al-KhazaliFoundedJuly 2006 (2006-07)IdeologyShia IslamismKhomeinism[1]Wilayat al-Faqih[2]Anti-Sunnism[3]Muhammad Sadiq al-Sadr Thought[4]Anti-Zionism[5]Anti-Americanism[6]Pan-Islamism[7]Anti-West[8]Anti-LGBT[9]Kazem al-Haeri Thought[10]Political positionRight-wing to far-rightReligionShia IslamNational affiliationF...

Dieser Artikel beschreibt die Bundesstraße 181 in Deutschland. Zur gleichnamigen Straße in Österreich siehe Achenseestraße. Vorlage:Infobox hochrangige Straße/Wartung/DE-B Bundesstraße 181 in Deutschland Karte Verlauf der B 181 Alle Koordinaten: OSM | WikiMap Basisdaten Betreiber: Deutschland Bundesrepublik Deutschland Straßenbeginn: Merseburg(51° 20′ 46″ N, 11° 59′ 9″ O51.34618311.985919) Straßenende: Leipzig(51° 20′...




![{\displaystyle Y=\{[x]:x\in X\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be56fce8ca3c36a3fe823a5bf46561e96aaeb74d)


![{\displaystyle {\mathcal {T}}_{\sim }=\{U\subseteq Y:\bigcup _{[x]\in U}[x]\in {\mathcal {T}}_{X}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f673d58c8110d2b99bde81aced90947e7f25ec)

![{\displaystyle p(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b8773dff8ad19fc5a8f33134a4da367b04fc0c)











































![{\displaystyle [x]_{X}\mapsto f_{\sim }([x]_{X})=[f(x)]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae7babc576c0e9d5a5cc5ca7560b5240e32cfdc)


![{\displaystyle [x]_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffaba5909fe85603ae2ac02a82d9a40023775ff4)
![{\displaystyle x\sim _{X}x'{\overset {\text{Hipótesis}}{\Rightarrow }}f(x)\sim _{Y}f(x')\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d73455deee1e90d6ddb2db714f008129202c0ce)
![{\displaystyle [y]_{Y}\in Y/{\sim _{Y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2e45e02deb31b84260019389f40a88eef35752)



![{\displaystyle [y]_{Y}=[f(x)]_{Y}=f_{\sim }([x]_{X})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a30145abf81e4020e7b57c6c2e74953bd48e1f)
![{\displaystyle [y]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0abce24890864d483c4b91a6197bf6ad8d13897)
![{\displaystyle f_{\sim }([x]_{X})=f_{\sim }([x']_{X})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72d22502468615e25c1efc7ef402ef6c72a8e9f2)
![{\displaystyle [x]_{X}=[x']_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/feb13314d07e316bd2bf3f180935182c268461ae)
![{\displaystyle f_{\sim }([x]_{X})=f_{\sim }([x']_{X})\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}\Rightarrow f(x)\sim _{Y}f(x'){\overset {\text{Hipótesis}}{\Rightarrow }}x\sim _{X}x'\Rightarrow [x]_{X}=[x']_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4006ac71740b67716f0cb2354e50921e5ad14804)




![{\displaystyle \pi _{Y}(f(x))=[f(x)]_{Y}{\overset {\text{def}}{=}}f_{\sim }([x]_{X})=f_{\sim }(\pi _{X}(x))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe3a31dc985d5d27a2a24b58fcf7d5727df129e)



![{\displaystyle I^{2}=[0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec146272a9e354527468cb89f8213c57e07c937e)

![{\displaystyle (0,y)\sim (1,y)\quad \forall x,y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6927082a10804df2a21ae760b47db2326ffde5cb)

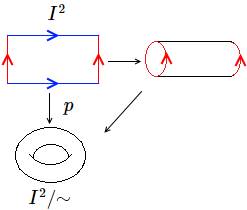

![{\displaystyle (0,y)\sim (1,1-y)\quad \forall y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1025c37e0ba2db5a59f2a2a835744b1ff7d7178)

![{\displaystyle (0,y)\sim (1,1-y)\quad \forall x,y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14976476db9bc4252b7394480d9d425f956bca2f)











