Teorema de la estadística del espín

El teorema de la estadística del espín o teorema de la correspondencia entre espín y estadística de la mecánica cuántica establece la relación directa entre el espín de una especie de partícula con la estadística a la que obedece. Fue demostrado por Fierz y Pauli en 1940, y requiere el formalismo de teoría cuántica de campos.

El teorema tiene algunos análogos imperfectos en teoría clásica de campos, recientemente se han dado algunas demostraciones formales totalmente rigurosas para el caso clásico y el cuántico.[1]​

Relación empírica y enunciado

  • El espín es un momento angular intrínseco (no asociado a su movimiento espacial) que posee toda partícula a nivel cuántico. Puede tomar valores enteros (0,1,2,...) o semienteros (1/2,3/2,...), en unidades de la constante de Planck .
  • La estadística de una especie de partículas determina su comportamiento colectivo:
    • Si pueden redistribuirse libremente en todas las configuraciones posibles del sistema, se denominan bosones. La función de onda de un sistema de bosones es simétrica bajo el intercambio de las coordenadas de dos partículas cualesquiera. Los fotones y las partículas alfa son bosones.
    • Si por el contrario obedecen el principio de exclusión de Pauli, que restringe estas configuraciones, se denominan fermiones. La función de onda de un sistema de fermiones es anti-simétrica bajo el intercambio de dos partículas, esto es, cambia de signo. Los protones, neutrones, y electrones son fermiones.

Estas dos propiedades están en aparencia totalmente descorrelacionadas. Sin embargo es un hecho experimental que todos los bosones poseen espín entero, mientras que los fermiones poseen espín semientero. Esta relación constituye el enunciado del teorema.

Consecuencias

Hay un par de fenómenos interesantes facilitados por los dos tipos de estadística. La distribución de Bose-Einstein describe los bosones en un condensado Bose-Einstein. Bajo una cierta temperatura, la mayoría de las partículas en un sistema bosónico estará en el estado fundamental (el de más baja energía). De ahí resultan propiedades inusuales como la superfluidez.

La distribución de Fermi-Dirac, que describe el comportamiento de los fermiones, también proporciona interesantes propiedades. Dado que sólo un único fermión puede ocupar un estado cuántico, el nivel fundamental de energía sólo puede ser ocupado por dos fermiones, con sus espines alineados de manera contraria. Así, incluso al cero absoluto de temperatura, el sistema tiene una cierta energía diferente de cero. Como resultado, un sistema fermiónico ejerce presión externa. Aún a temperaturas diferentes de cero absoluto, dicha presión existe. Esta presión es la responsable de que ciertas estrellas masivas no puedan colapsar debido a la gravedad (ver enana blanca, estrella de neutrones, y agujero negro).

Espacio-tiempo curvo

En el espacio-tiempo curvo, aparece una conexión entre estadística y dinámica que no está presente en el espacio-tiempo de Minkowski. La estadística está determinada por el álgebra de operadores de creación: los operadores de que conmutan dan a la estadística de Bose-Einstein y los operadores anticonmutadores dan a la estadística de Fermi-Dirac.[2]​

Referencias

  1. ↑ Greaves, H.; Thomas, T. (2014). «On the CPT theorem». Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 45: 46-65. 
  2. ↑ Parker, L.; Toms, D. (2009). Quantum field theory in curved spacetime: quantized fields and gravity. Cambridge university press. p. 54. 

Read other articles:

Dear Nathan

Dear NathanSutradaraIndra GunawanProduserGope T. SamtaniSkenarioBagus BramantiGea RexyBerdasarkanDear Nathanoleh Erisca FebrianiPemeran Amanda Rawles Jefri Nichol Surya Saputra Rayn Wijaya Diandra Agatha Beby Tsabina Denira Wiraguna Adi Virsa Prayudi Penata musikAndhika TriyadiSinematograferIvan Anwal PanePenyuntingRyan PurwokoPerusahaanproduksiRapi FilmsDistributorNetflixTanggal rilis 23 Maret 2017 (2017-03-23) (Indonesia) Durasi99 menitNegara IndonesiaBahasaBahasa Indone...

 

List of Kathak dancers

This is a list of the Sangeet Natak Akademi awards for the Indian classical dance form of Kathak, as well as gurus and well-known performers. Sangeet Natak Akademi awardees Dancer Shovana Narayan [1] Shambhu Maharaj 1955 Sunder Prasad 1959 Mohanrao Kallianpurkar 1962 Birju Maharaj 1964 Damayanti Joshi 1968 Sitara Devi 1969 Roshan Kumari 1975 Rohini Bhate 1979 Kumudini Lakhia 1982 Durga Lal 1984 Uma Sharma 1987 Maya Rao 1989 Rani Karnaa 1996 Shovana Narayan 1999-2000 Rajendra Gangani ...

 

List of cities conquered by the Ottoman Empire

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of cities conquered by the Ottoman Empire – news · newspapers · books · scholar · JSTOR (June 2011) (Learn how and when to remove this template message) Part of a series on the Military of theOttoman Empire Classical army (1451–1826) Kapıkulu Janissari...

Katsuya Okada

Katsuya Okada岡田 克也 Deputi Perdana Menteri JepangMasa jabatan13 Januari 2012 – 26 Desember 2012Perdana MenteriYoshihiko Noda PendahuluKosongTerakhir dipegang oleh Naoto KanPenggantiTarō AsōMenteri Urusan Luar NegeriMasa jabatan16 September 2009 – 17 September 2010Perdana MenteriYukio HatoyamaNaoto Kan PendahuluHirofumi NakasonePenggantiSeiji Maehara Informasi pribadiLahir岡田克也 (Okada Katsuyacode: ja is deprecated )14 Juli 1953 (umur 70)Yokkaichi, Mie...

 

History of the Cleveland Browns

This article may be too long to read and navigate comfortably. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (February 2024) Game program depicting the Brownie elf, the team's primary mascot in its successful early years. From the Browns' first game on September 6, 1946, against the Miami Seahawks. The history of the Cleveland Browns American football team began in 1944 when taxi-cab magnate Arthur B....

 

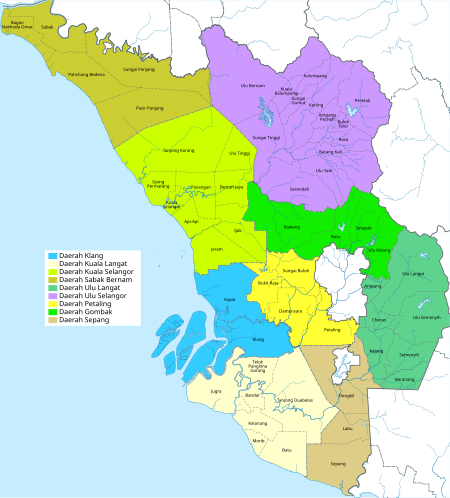
Taman Keramat

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Taman Keramat – news · newspapers · books · scholar · JSTOR (February 2016) (Learn how and when to remove this template message) Township in Selangor, MalaysiaKeramatTownshipTaman KeramatKeramatKeramat in Selangor, Malay Peninsular and MalaysiaShow map of SelangorKeramatKeramat ...

AWB Limited

Former Australian Wheat Board AWB LimitedFormerlyAustralian Wheat BoardTraded asASX: AWBIndustryGrainFounded1939FounderGovernment of AustraliaDefunct2010HeadquartersMelbourne, AustraliaRevenue$5.5 billion (2010)Operating income$407 million (2010)Net income$13 million (2010)Number of employees2,200Websitewww.awb.com.au AWB Limited was a major grain marketing organisation based in Australia. Founded in 1939 by the Government of Australia as the Australian Wheat Board, in 199...

 

Cinnamomum burmanni

Species of flowering plant Indonesian cinnamon Conservation status Least Concern  (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Magnoliids Order: Laurales Family: Lauraceae Genus: Cinnamomum Species: C. burmanni Binomial name Cinnamomum burmanni(Nees & T.Nees) Blume[2] Synonyms[2] Synonymy Cinnamomum ammannii Lukman. Cinnamomum burmanni var. angustifolium Meisn. Cinnamomum burmanni var. chinense (B...

 

Mohammed Hasan Alwan

Saudi Arabian novelist (born 1979) Mohammed Hasan AlwanBorn(1979-08-27)27 August 1979Riyadh, Saudi ArabiaNationalitySaudi ArabianGenreNovels, short stories Mohammed Hasan Alwan (born 27 August 1979) is a Saudi Arabian novelist.[1] He was born in Riyadh and studied Computer Information Systems at King Saud University, obtaining a bachelor's degree in 2002. He also obtained an MBA from the University of Portland, Oregon in 2008 and Ph.D from Carleton University, Ottawa in 2016.[2 ...

Sean Astin

Questa voce o sezione sugli argomenti registi statunitensi e attori statunitensi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. Sean Astin al San Diego Comic-Con International nel 2014 Sean Astin, pseudonimo di Sean Patrick Duke (Santa Monica, 25 febbraio 1971) è un attore e regista statunitense, c...

 

艾哈迈德·哈桑·贝克尔

此條目可参照英語維基百科相應條目来扩充。 (2022年1月31日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 艾哈迈德·哈桑·贝克尔أحمد حسن البكر第4任伊拉克总统任期1968年7月17日—1979年7月16日副总统萨达姆·侯...

 

I Hope They Serve Beer in Hell

Book by Tucker Max For the film based on the novel, see I Hope They Serve Beer in Hell (film). I Hope They Serve Beer in Hell First editionAuthorTucker MaxCover artistErin TylerCountryUnited StatesLanguageEnglishGenreNon-Fiction, fratirePublisherCitadel PressPublication dateJanuary 2006Pages277 ppISBN978-0-8065-2728-4Preceded byBelligerence and Debauchery: The Tucker Max Stories Followed byAssholes Finish First  I Hope They Serve Beer in Hell is a book of autobiograph...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

 

Domingos Sequeira

Portuguese painter (1768–1837) Domingos SequeiraSelf-Portrait by Domingos SequeiraBornDomingos António de Sequeira(1768-03-10)10 March 1768Lisbon, Kingdom of PortugalDied8 March 1837(1837-03-08) (aged 68)Rome, Papal StatesNationalityPortugueseKnown forFine PaintingMovementNeoclassicism Domingos António de Sequeira (Lisbon; 10 March 1768 – Rome; 8 March 1837) was a famous Portuguese painter at the Royal Court of King John VI of Portugal. Biography He was born in Be...

 

Perceptual robotics

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Perceptual robotics – news · newspapers · books · scholar · JSTOR (December 2007) (Learn how and when to remove this message) Perceptual robotics is an interdisciplinary science linking Robotics and Neuroscience. It investigates biologically motivated robot control strategies, concentrating on perceptual r...

Arnos

Arnoscomune Arnos – VedutaIl Municipio LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Pirenei Atlantici ArrondissementPau CantoneArtix et Pays de Soubestre TerritorioCoordinate43°27′N 0°32′W43°27′N, 0°32′W (Arnos) Altitudine133–232 m s.l.m. Superficie5,69 km² Abitanti113[1] (2017) Densità19,86 ab./km² Altre informazioniCod. postale64370 Fuso orarioUTC+1 Codice INSEE64048 CartografiaArnos Sito istituzionaleModifica dati...

 

Iran–Turkey border

International border Iran-Turkey border مرز ترکیه و ایران İran–Türkiye sınırıCharacteristicsEntities Iran  TurkeyLength560 km (350 mi)[1] The Iran–Turkey border (Persian: مرز ترکیه و ایران; Turkish: İran–Türkiye sınırı) is 534 kilometres (332 miles) in length, and runs from the tripoint with Azerbaijan in the north to the tripoint with Iraq in the south.[2] Description Map of the Iran-Turkey border by the United S...

 

Дубнов, Семён Маркович

В Википедии есть статьи о других людях с фамилией Дубнов. Семён Маркович ДубновШи́мен Ме́ерович Ду́бнов Дата рождения 10 сентября 1860(1860-09-10) Место рождения Мстиславль, Могилевская губерния, Российская империя Дата смерти 8 декабря 1941(1941-12-08) (81 год) Место смерти Рига, Р�...

Eosinophil

Variety of white blood cells Eosinophil3D rendering of eosinophilEosinophil under the microscope (400×) from a peripheral blood smear. Red blood cells surround the eosinophil, two platelets at the top left corner.DetailsPronunciation/ˌiːoʊˈsɪnəfɪl/)[1]SystemImmune systemIdentifiersMeSHD004804THH2.00.04.1.02017 FMA62861Anatomical terms of microanatomy[edit on Wikidata] Eosinophils, sometimes called eosinophiles or, less commonly, acidophils, are a variety of white blood cel...

 

Chloe (attrice pornografica)

ChloeDati biograficiNazionalità Stati Uniti Dati fisiciAltezza165 cm Peso52 kg EtniaCaucasica Occhimarroni Capellirossi Seno naturalesì Misure32AA-25-34 Dati professionaliAltri pseudonimiChloe Nicole, Chloe Nichole, Chloe Nichols, Chloe Nicholle Film girati 546 come attrice 18 come regista Modifica dati su Wikidata · Manuale Chloe Hoffman (Thousand Oaks, 14 novembre 1971) è un'ex attrice pornografica, modella e regista pornografica statunitense. Indice 1 Biografia 2 Carriera...