Sucesión de Lucas
|
Read other articles:

Barbara BarrieBarrie di Barney Miller tahun 1975 bersama Hal LindenLahirBarbara Ann Berman23 Mei 1931 (umur 92)Chicago, Illinois, A.S.AlmamaterUniversitas Texas (B.F.A., 1952)PekerjaanAktris, penyanyi, penulisTahun aktif1953–sekarangSuami/istriJay Harnick (m. 1964; meninggal 2007)Anak2 Barbara Barrie (nee Barbara Ann Berman; lahir 23 Mei 1931) adalah seorang aktris film, panggung dan televisi Amerika. Dia juga seorang penulis.&#...

Arhur Holly ComptonLahir19 Februari 1859Ohio, USAMeninggal15 Maret 1962Berkeley, CaliforniaAlmamaterCollege of Wooster (1913)Princeton University (1916)ZamanFilsafat abad ke-19Suami/istriBey Charity McCloskey (1916)Orang tuaElias Compton Arthur Holly Compton (10 September 1892 – 15 Maret 1962) ialah fisikawan Amerika Serikat yang menerima Penghargaan Nobel dalam Fisika atas sumbangannya dalam penemuan sebuah efek yang dinamai menurut namanya (efek Compton). Dil...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this template message) Wheeled all-terrain vehicle VBL Gladiador TypeWheeled all-terrain vehiclePlace of origin BrazilSpecificationsMass3.5tLength3.80 m (4.00 m long version)Width2.02 mHeight1.70 mCrew2-3ArmourSTANAG...

Kincir angin Pitstone, dipercaya sebagai kincir angin tertua di Britania Raya Kincir angin adalah sebuah alat yang mampu memanfaatkan kekuatan angin untuk diubah menjadi kekuatan mekanik. Dari proses itu memberikan kemudahan berbagai kegiatan manusia yang memerlukan tenaga yang besar seperti memompa air untuk mengairi sawah atau menggiling biji-bijian. Kincir angin modern adalah mesin yang digunakan untuk menghasilkan energi listrik, disebut juga dengan turbin angin. Turbin angin kebanyakan d...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Dewan Menteri USSRСовет Министров СССРBekas markas besar Dewan MenteriInformasi lembagaDibentuk1946Nomenklatur lembaga sebelumnyaDewan Komisar RakyatDibubarka...

Pour les articles homonymes, voir Macerata (homonymie). Macerata Armoiries Clochers du centre historique. Administration Pays Italie Région Marches Province Macerata Code postal 62100 Code ISTAT 043023 Code cadastral E783 Préfixe tel. 0733 Démographie Gentilé maceratesi Population 41 200 hab. (31-12-2019[1]) Densité 448 hab./km2 Géographie Coordonnées 43° 18′ 00″ nord, 13° 27′ 00″ est Altitude Min. 315 mMax. 315&#...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

الهوبيت: رحلة غير متوقعةThe Hobbit: An Unexpected Journey (بالإنجليزية) الملصق الدعائي للفيلممعلومات عامةالتصنيف فيلم ثلاثي الأبعاد الصنف الفني القائمة ... فيلم فنتازيا — فيلم مغامرة — فيلم صيد كنوز — فيلم أكشن — فيلم ملحمي — فيلم مقتبس من عمل أدبي تاريخ الصدور 12 ديسمبر، 2012مدة العرض ...

Aristotle MountainsLocation of Aristotle Mountains on the Antarctic Peninsula Highest pointPeakMadrid DomeElevation1,647 m (5,404 ft)DimensionsLength62 km (39 mi) SW-NEWidth44 km (27 mi) NW-SEGeographyContinentAntarcticaRegionGraham LandRange coordinates65°35′S 62°28′W / 65.583°S 62.467°W / -65.583; -62.467Borders onBruce Plateau Aristotle Mountains is the fan-shaped sequence of ridges spreading east-northeastwards fro...

الاحتجاجات البحرينية 2011 جزء من ثورات الربيع العربي التاريخ 14 فبراير 2011 – 30 مارس 2011 المكان البحرين النتيجة النهائية دخول درع الجزيرة لدوار اللؤلؤة (دوار مجلس التعاون) وفض الاعتصام وقمع الانتفاضة. استمرار المظاهرات العرضية. الأسباب الإلهام من الاحتجاجات الإقليمية ال...

Малое Моребур. Нарин далай Малое Море Характеристики Ширина5—16 км Длина70 км Расположение 53°15′ с. ш. 107°15′ в. д.HGЯO Вышестоящая акваторияБайкал Страна Россия Субъект РФИркутская область РайонОльхонский район Малое Море Медиафайлы на Викискладе �...

Film and recording complex Jim Henson Company LotMain Gates, 2006Location1416 N. La Brea AvenueHollywood, Los Angeles, California, U.S.Coordinates34°5′47″N 118°20′35″W / 34.09639°N 118.34306°W / 34.09639; -118.34306Area80,000 sq ft (7,400 m2)Built1917; 107 years ago (1917)Governing bodyPrivateOwnerThe Jim Henson Company Los Angeles Historic-Cultural MonumentDesignated1969[1]Reference no.58 Location of Jim Henson...

Mission: Yozakura FamilyGambar sampul manga volume pertama夜桜さんちの大作戦(Youzakura san Chi no Daisakusen)GenreKomediMata-mataKomedi romantis MangaPengarangHitsuji Gondaira (権平ひつじ)PenerbitShueishaPenerbit bahasa InggrisNA Viz MediaImprintJump ComicsMajalahWeekly Shōnen JumpDemografiShōnenTerbit26 Agustus 2019 – sekarangVolume23 (Daftar volume) Seri animeSutradaraMirai Minato (湊未来)ProduserGenta Ozaki (尾崎源太) (NBCUniversal Entertainment Japan)Hiroyuki Aoi ...

American college football season 2003 Kansas Jayhawks footballTangerine Bowl, L 26–56 vs. NC StateConferenceBig 12 ConferenceDivisionNorthRecord6–7 (3–5 Big 12)Head coachMark Mangino (2nd season)Offensive coordinatorNick Quartaro (2nd season)Defensive coordinatorBill Young (2nd season)Home stadiumMemorial Stadium(Capacity: 50,071)Seasons← 20022004 → 2003 Big 12 Conference football standings vte Conf Overall Team W L W...
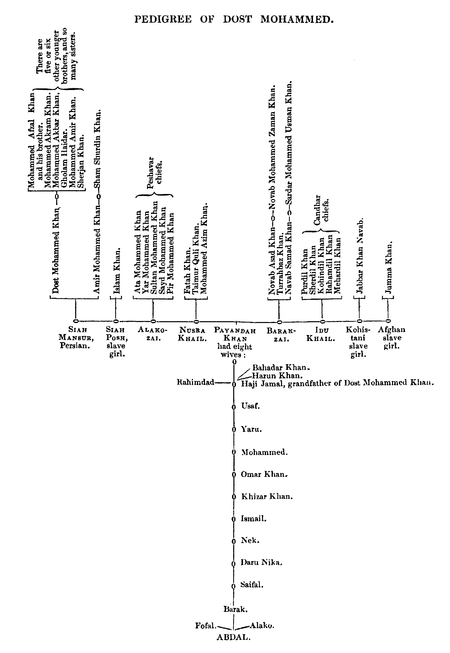
Durrani Pashtun tribe Part of a series on the History of Afghanistan Timeline Ancient Indus Valley Civilisation 2200–1800 BC Oxus Civilization 2100–1800 BC Gandhara Kingdom 1500–535 BC Median Empire 728–550 BC Achaemenid Empire 550–330 BC Macedonian Empire 330–312 BC Seleucid Empire 312–150 BC Maurya Empire 305–180 BC Greco-Bactrian Kingdom 256–125 BC Parthian Empire 247 BC–224 AD Indo-Greek Kingdom 180–130 BC Indo-Scythian Kingdom 155–80? BC Kushan Empire 135 BC – 2...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Polyrhaphis pilosa Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Polyrhaphis Spesies: Polyrhaphis pilosa Polyrhaphis pilosa adalah spesies kumbang tanduk panjang yang tergolong famil...

العلاقات الأرمينية التشادية أرمينيا تشاد أرمينيا تشاد تعديل مصدري - تعديل العلاقات الأرمينية التشادية هي العلاقات الثنائية التي تجمع بين أرمينيا وتشاد.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة أرمي�...

American arts and culture magazine Film CommentCover of the May/June 2010 edition, celebrating the 50th year anniversary of Jean-Luc Godard's Breathless (1960)EditorDevika Girish and Clinton KruteCategoriesFilmFrequencyBimonthlyCirculation17,626 (2018)PublisherFilm at Lincoln CenterFirst issue1962CountryUnited StatesBased inNew York CityWebsitefilmcomment.comISSN0015-119X Film Comment is the official publication of Film at Lincoln Center. It features reviews and analysis of mainstream, art-ho...

For other uses, see Fram (disambiguation). Norwegian sports club Football clubFram LarvikFull nameIdrettsforeningen FramNickname(s)FramFounded15 January 1894; 130 years ago (1894-01-15)GroundFramparkenHead coachHaakon LunovLeague3. divisjon20232. divisjon group 1, 14th of 14 (relegated)WebsiteClub website Home colours Away colours Idrettsforeningen Fram, better known as Fram Larvik to distinguish it from other sport clubs, is a sports club from Torstrand in Larvik, Norway. I...

Army from 1861 to 1946 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Royal Italian Army – news · newspapers · books · scholar · JSTOR (July 2011) (Learn how and when to remove this message) Royal Italian ArmyRegio Esercito ItalianoWar Flag of the Regio EsercitoActive1861–1946Country Kingdom of Italy...






























































