Prueba por contradicción
|
Read other articles:

Hindu temple in Pondicherry, India Tirunallar Dharbaranyeswarar TempleDharbaranyamReligionAffiliationHinduismDistrictKaraikkalDeityDharbaranyeswarar(Shiva), Shani,Bogamartha Poonmulaiyaal(Parvati)LocationLocationTirunallarStatePondicherryCountryIndiaLocation in Tamil NaduGeographic coordinates10°55′32″N 79°47′32″E / 10.92556°N 79.79222°E / 10.92556; 79.79222ArchitectureTypeDravidian architecture Tirunallar Saniswaran Temple or Dharbaranyeswarar Temple is a...

Sporting event delegationEgypt at the2004 Summer OlympicsIOC codeEGYNOCEgyptian Olympic CommitteeWebsitewww.egyptianolympic.org (in Arabic and English)in AthensCompetitors97 in 17 sportsFlag bearer Ali Ibrahim[1][2]MedalsRanked 46th Gold 1 Silver 1 Bronze 3 Total 5 Summer Olympics appearances (overview)1912192019241928193219361948195219561960–1964196819721976198019841988199219962000200420082012201620202024Other related appearances1906 Intercalated Games –––�...

Argentine educational television channel For the Paul Gonsalves album, see Encuentro (album). This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Encuentro – news · newspapers · books · scholar · JSTOR (June 2017) (Learn how and when to remove this template message) EncuentroCityBuenos AiresChannelsDigital: 22.01 (UHF)BrandingEnc...

Papa Sisto II24º papa della Chiesa cattolicaElezione30 agosto 257 Fine pontificato6 agosto 258(0 anni e 341 giorni) Predecessorepapa Stefano I Successorepapa Dionisio NascitaGrecia? MorteRoma, 6 agosto 258 SepolturaBasilica di San Sisto Vecchio Manuale San Sisto IISisto II dipinto da Sandro Botticelli Papa e martire NascitaGrecia? MorteRoma, 6 agosto 258 Venerato daTutte le Chiese che ammettono il culto dei santi Beatificazione15 ottobre 1675 da papa Clemente X Can...

Antoine Arnauld Antoine Arnauld, soprannominato dai contemporanei il Grande Arnauld, per distinguerlo da suo padre (Parigi, 5 febbraio 1612 – Bruxelles, 8 agosto 1694), è stato un teologo, filosofo e matematico francese, uno dei capifila del giansenismo e avversario dei Gesuiti[1]. Indice 1 Biografia 2 Teologo, filosofo e matematico 3 Opere principali 4 Edizioni 5 Note 6 Altri progetti 7 Collegamenti esterni Biografia Era il ventesimo e più piccolo dei figli di Antoine Arnauld, pr...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Indonesian chicken noodle dish Bakmi ayamBakmi ayam with mushroom, chinese cabbage and chicken broth soup.Alternative namesMi ayam cincang, bakmi ayam, Chicken noodlesCourseMain coursePlace of originIndonesia[1]Region or stateNationwideAssociated cuisineIndonesiaServing temperatureHotMain ingredientsNoodle, chicken meat, soy sauce, garlic, cooking oil (from chicken fat or vegetable oil), chicken broth, chinese cabbage, scallionsFood energy(per serving)1 bowl of mie ayam contains 500 c...

Olivier Messiaen tahun 1986 Olivier Eugène Prosper Charles Messiaen[1] (UK /ˈmɛsiæ̃/,[2] US /mɛˈsjæ̃, meɪˈsjæ̃, mɛˈsjɒ̃/;[3][4][5] bahasa Prancis: [ɔlivje mɛsjɑ̃]; 10 Desember 1908 – 27 April 1992) adalah seorang komponis Prancis, organis, dan ornitologis, ia merupakan salah satu komposer utama pada abad ke-20. Catatan ^ Griffiths 2001. ^ Messiaen, Olivier. Lexico UK Dictionary. Oxford University Press. Diakses tanggal A...
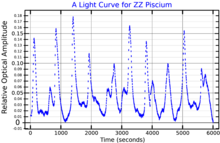
White dwarf which undergoes characteristic variability G29-38 Artist's impression of G29-38 and its debris disk Observation dataEpoch J2000.0 Equinox J2000.0 Constellation Pisces Right ascension 23h 28m 47.6365s[1] Declination +05° 14′ 54.235″[1] Apparent magnitude (V) 13.03[2] Characteristics Spectral type DAV4.4[2] U−B color index −0.63[2] B−V color index 0.14[2]...

Matthew Kneale (Londra, 24 novembre 1960) è uno scrittore britannico, conosciuto in particolare per il suo romanzo Il passeggero inglese. Indice 1 Biografia 2 Opere 2.1 Narrativa 2.2 Saggistica 3 Note 4 Collegamenti esterni Biografia Figlio degli scrittori Nigel Kneale[1] e Judith Kerr[2], ha frequentato la Latymer Upper School di Londra[3], e in seguito ha studiato storia moderna al Magdalen College (Oxford)[4], prima di trascorrere un anno in Giappone, dove ...

У этого термина существуют и другие значения, см. Тур. Запрос «Bos taurus primigenius» перенаправляется сюда; см. также другие значения. † Тур Скелет тура Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:В...

日語寫法日語原文日本標準時假名にほんひょうじゅんじ平文式罗马字Nihon Hyōjunji此條目可参照日語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。兵庫縣明石市的明石市立天文科學館(...

Dong Biwu董必武Dong Biwu Presiden Dewan Rakyat Tertinggi Republik Rakyat TiongkokMasa jabatan1954–1959PendahuluShen JunruPenggantiXie JuezaiWakil Pemimpin Republik Rakyat TiongkokMasa jabatan27 April 1959 – 17 Januari 1975PresidenLiu ShaoqiSoong Ching-lingDirinya sendiri (acting)PemimpinMao ZedongPendahuluZhu DePenggantiUlanhuPemimpin Republik Rakyat Tiongkok(acting)Masa jabatan31 Oktober 1968 – 17 Januari 1975Perdana MenteriZhou EnlaiPendahuluLiu ShaoqiPenggantiJabatan dibuat(Li Xia...

Japanese term for an attractive young man For the film, see Bishonen (film). Bishy redirects here. For the radial route in York, England, see Bishy Road. Gackt, a Japanese singer-songwriter, is considered to be one of the living manifestations of the Bishōnen phenomenon.[1][2] Bishōnen (美少年, IPA: [bʲiɕo̞ꜜːnẽ̞ɴ] ⓘ; also transliterated bishounen) is a Japanese term literally meaning beautiful youth (boy) and describes an aesthetic that can be found in...

Robbie Kruse Informasi pribadiNama lengkap Robbie Thomas KruseTanggal lahir 5 Oktober 1988 (umur 35)Tempat lahir Brisbane, AustraliaTinggi 1,81 m (5 ft 11+1⁄2 in)Posisi bermain PenyerangInformasi klubKlub saat ini VfB StuttgartNomor 9Karier junior Albany Creek2004–2005 QAS2005–2006 AISKarier senior*Tahun Tim Tampil (Gol)2007–2009 Brisbane Roar 28 (4)2009–2011 Melbourne Victory 39 (16)2011–2013 Fortuna Düsseldorf 41 (4)2013– Bayer Leverkusen 21 (2)2015�...

U.S. House district for Florida FL-12 redirects here. For the state road, see Florida State Road 12. Florida's 12th congressional districtInteractive map of district boundaries since January 3, 2023Representative Gus BilirakisR–Palm HarborArea1,069[1] sq mi (2,770 km2)Distribution93.09% urban[2]6.91% ruralPopulation (2022)806,076[3]Median householdincome$59,804[3]Ethnicity75.3% White13.6% Hispanic4.4% Black4.1% Two or more races2.0% Asian...

Spanish free-to-air television channel TVE2 redirects here. For the Finnish locomotive class, see VR Class Tve2. Television channel La 2CountrySpainBroadcast areaNationwide, Andorra, Gibraltar, also parts of France and Portugal, and WorldwideNetworkTelevisión Española (TVE)HeadquartersPrado del Rey, Pozuelo de Alarcón (Madrid)ProgrammingLanguage(s)SpanishPicture format1080i HDTVOwnershipOwnerRadiotelevisión Española (RTVE)Sister channelsLa 1Clan24hTeledeporteTVE InternacionalStar TVE HDH...
Location of Franklin County in Indiana This is a list of the National Register of Historic Places listings in Franklin County, Indiana. This is intended to be a complete list of the properties and districts on the National Register of Historic Places in Franklin County, Indiana, United States. Latitude and longitude coordinates are provided for many National Register properties and districts; these locations may be seen together in a map.[1] There are 14 properties and districts list...

La bagnante di ValpinçonAutoreJean-Auguste-Dominique Ingres Data1808 Tecnicaolio su tela Dimensioni146×97,5 cm UbicazioneMuseo del Louvre, Parigi La bagnante di Valpinçon (La Baigneuse Valpinçon), noto anche come La grande bagnante (Grande Baigneuse), è un dipinto di Jean-Auguste-Dominique Ingres (146 cm × 97,5 cm), probabilmente fra i più noti del pittore, realizzato nel 1808. Indice 1 Storia e descrizione 2 Note 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Storia e des...

Questa voce sugli argomenti film sentimentali e film commedia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. I Love MoviesCillian Murphy e Lucy Liu in una scena del filmTitolo originaleWatching the Detectives Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno2007 Durata91 min Generecommedia, sentimentale RegiaPaul Soter SceneggiaturaPaul Soter ProduttoreCeline Rattray, Reag...






















