Proceso de Bernoulli
|
Read other articles:

Patrick DeLacyLahir(1835-11-25)25 November 1835Carbondale, PennsylvaniaMeninggal27 April 1915(1915-04-27) (umur 79)PennsylvaniaDikebumikanSaint Catherine's Cemetery, Moscow, PennsylvaniaPengabdian Amerika SerikatDinas/cabangUnited States ArmyUnion ArmyPangkatKapten (keluar dari ketenaraan sebagai letnan)Kesatuan 143rd Pennsylvania Volunteer Infantry Regiment - Company APenghargaan Medal of Honor Civil War Campaign Medal Patrick DeLacy (25 November 1835 – 27 April 191...

Monika, pemimpin kru tari PROWDMON melakukan wawancara pada tahun 2021 PROWDMON merupakan kru tari wanita yang menjadi salah satu peserta acara survival Mnet Street Woman Fighter dan telah aktif di industri hiburan Korea selama hampir 20 tahun. Pada acara survival Street Woman Fighter, kru tari ini menduduki peringkat keenam dari delapan kru tari.[1] Penampilan Pada 19 Oktober 2021, Netflix Korea merilis video penampilan kru tari PROWDMON untuk K-Drama orisinal terbaru mereka My Name....

Seorang pandu sedang menaiki kapal yang akan dipandu yang sedang berlayar Signal flag H(hotel) - Pandu diatas kapal Kapal pandu adalah kapal yang memandu kapal besar masuk kedalam pelabuhan melalui alur yang berbahaya dan ramai sampai sandar di dermaga. Merupakan salah satu jabatan tertua yang sangat penting untuk meningkatkan keselamatan pelayaran. Lihat pula Kapal pandu (pilot boat) adalah kapal/ boat yang digunakan untuk mengantar/ menjemput petugas pandu yang akan memandu/selesai melakuka...

Erich KulkaKulka di 1993LahirErich Schön(1911-02-18)18 Februari 1911Vsetín, Austria-HungaryMeninggal12 Juli 1995(1995-07-12) (umur 84)Yerusalem, IsraelWarga negaraCeko (1911), Israel (1968)PekerjaanPenulis, sejarawan, jurnalis Erich Kulka (18 Februari 1911 – 12 Juli 1995) adalah seorang penulis, sejarawan, dan jurnalis Czech-Israel yang selamat dari Holokaus. Setelah Perang Dunia II, ia menjadikan penelitian tentang Holokaus dan penyebaran fakta-fakta tentangnya sebagai misi hi...

Halaman ini berisi artikel tentang gugus fungsional organik aril. Untuk artikel lainnya dengan nama yang serupa, lihat ariel (disambiguasi). Fenil merupakan suatu gugus aril paling sederhana, pada gambar ini terikat dengan suatu gugus R. Dalam konteks molekul organik, aril merupakan semua gugus fungsional atau substituen yang berasal dari suatu cincin aromatik, biasanya suatu hidrokarbon aromatik, dapat berupa fenil, naftil, indolil, dan lain sebagainya. (lihat tata nama senyawa kimia).[1...

BakoolWilayahLokasi di Somalia.Koordinat: 4°20′47″N 43°32′59″E / 4.34639°N 43.54972°E / 4.34639; 43.54972Koordinat: 4°20′47″N 43°32′59″E / 4.34639°N 43.54972°E / 4.34639; 43.54972Negara SomaliaIbu kotaXuddurZona waktuUTC+3 (EAT)Kode area teleponBakoolHDI (2017)0.287[1]rendah Bakool adalah sebuah daerah (gobolka) di Somalia bagian tengah. Ibu kotanya ialah Xuddur. Bakool berbatasan dengan Ethiopia dan daerah S...

الأميرة إليزابيث أميرة كلارنس معلومات شخصية الميلاد 10 ديسمبر 1820(1820-12-10)قصر سانت جيمس الوفاة 4 مارس 1821 (0 سنة) قصر سانت جيمس سبب الوفاة انسداد معوي مكان الدفن كنيسة القديس جورج مواطنة المملكة المتحدة لبريطانيا العظمى وأيرلندا الأب ويليام الرابع ملك ال...

Pour les articles homonymes, voir Renfrew. Cet article est une ébauche concernant une localité écossaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Renfrew en écossais : Rinn Friù Centre-ville et hôtel de ville de Renfrew Administration Pays Royaume-Uni Nation Écosse Council area Renfrewshire Ancien comté Renfrewshire Région de lieutenance Renfrewshire Force de police Police Scotland Incendie...

Australian media company Ten Network Holdings Ltd.Company typeSubsidiaryIndustryMediaFounded31 March 1998; 26 years ago (1998-03-31)Headquarters1 Saunders Street, Pyrmont, New South Wales, AustraliaKey peopleBeverley McGarvey (CEO and President)David Gordon (chairman)ProductsTelevisionParentParamount Networks UK & AustraliaWebsitewww.paramountanz.com.au Ten Network Holdings Ltd., commonly referred as Paramount Australia & New Zealand, is a major media company in Aust...

For the community in Ohio, see Mill Rock, Ohio. Island in New York City Mill RockMill Rock as seen from Wards Island Bridge. The Citicorp Building and Big Allis are visible in the background.Mill RockGeographyLocationEast River, New York County, New York, USACoordinates40°46′51″N 73°56′18″W / 40.7807°N 73.9384°W / 40.7807; -73.9384Area3.5 ha (8.6 acres)[1]AdministrationUnited StatesStateNew YorkCityNew York CityBoroughManhattan Mill Rock fort&#...

Pemandangan Acarigua pada tahun 2018 Kerusuhan penjara Acarigua 2019 terjadi pada 24 Mei 2019 di penjara kantor polisi PoliPáez di Acarigua, Portuguesa, Venezuela. Kerusuhan ini dipicu oleh pelarangan kunjungan keluarga tahanan pada beberapa hari sebelum kejadian. Peristiwa ini mengakibatkan 29 orang tahanan tewas dan 19 polisi terluka. Rujukan Twenty-nine detainees killed in Venezuela police station cellblock riot. Reuters. 25 Mei 2019. Families demand answers after 29 inmates die in ...

Anarchism movement in Indonesia Anarchist Movement in Jakarta Part of a series onAnarchism History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Free-market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Agorism Illegalism Insurrectionary Communization Expropriative Pacifist Platformism Especifismo Relationship...

Gulab SinghRaja JammuBerkuasa16 Juni 1822—16 Maret 1846[1]PendahuluKishore SinghMaharaja Jammu dan KashmirBerkuasa16 Maret 1846—20 Februari 1856[2]PenerusRanbir SinghWazir Kemaharajaan SikhMasa jabatan31 Januari 1846 – 9 Maret 1846PendahuluLal SinghKelahiran(1792-10-18)18 Oktober 1792JammuKematian30 Juni 1857(1857-06-30) (umur 64)WangsaDinasti DograNama lengkapGulab SinghAyahMian Kishore SinghIstriNihal KourAnakSohan SinghUdam SinghRanbir SinghAgamaHindu Gulab Singh...

Moldova 1CaractéristiquesCréation 30 avril 1958Propriétaire Teleradio-MoldovaSlogan Împreună de la începuturi ! (Ensemble depuis le début !)Langue Roumain et RussePays MoldavieStatut Généraliste nationale publiqueSiège social ChișinăuAncien nom Canalul 1 Moldova TVSite web Site officielDiffusionAnalogique VHF SECAM Chaîne n° 1Numérique ?Satellite Thor 3Câble SunCommunications Moldtelecom: Chaîne n°1modifier - modifier le code - modifier Wikidata Moldova 1 est une c...

German association football club This article is about the football club. For the German royal family, see Holstein-Kiel. Football clubHolstein KielFull nameKieler SportvereinigungHolstein von 1900 e.V.Nickname(s)Die Störche (The Storks)[citation needed]Founded7 October 1900; 123 years ago (1900-10-07)GroundHolstein-StadionCapacity15,034[citation needed]Executive directorWolfgang Schwenke[citation needed]PresidentSteffen Schneekloth[citation need...

Ketua Menteri Haryana(Haryana ke Mukhya Mantri)PetahanaManohar Lal Khattarsejak 26 Oktober 2014Ditunjuk olehGubernur HaryanaPejabat perdanaB. D. SharmaDibentuk1 November 1966 Ketua Menteri Haryana adalah ketua eksekutif dari negara bagian India utara Haryana. Sesuai dengan Konstitusi India, gubernur adalah seorang kepala de jure negara bagian, namun otoritas eksekutif de facto dipegang ketua menteri. Setelah pemilihan-pemilihan dari Mahkamah Legislatif Haryana, gubernur negara bagian ter...
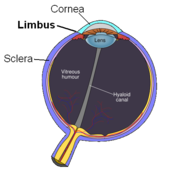
Method of administration of drugs into the eye by injection with a fine needle An anatomical diagram of the human eye, showing vitreous humor in the vitreous chamber. Intravitreal injection is the method of administration of drugs into the eye by injection with a fine needle. The medication will be directly applied into the vitreous humor.[1] It is used to treat various eye diseases, such as age-related macular degeneration (AMD), diabetic retinopathy, and infections inside the eye su...

Part of a series onEarly Buddhism Scriptures Early Buddhist Texts (EBT) Tripiṭaka Nikayas Āgamas Gandhāran EBTs Prātimokṣa Abhidharma Jatakas Avadanas Mahāvastu Śālistamba Sūtra Tibetan EBTs in the Kangyur Early sangha Gautama Buddha Sāriputta Mahāmoggallāna Mahāpajāpatī Gotamī Mahakasyapa Ānanda Upāli Mahākātyāyana Devadatta Anāthapiṇḍika Pre-sectarian Buddhism Kingdom of Magadha Ashoka Moggaliputtatissa Buddhist councils Early Buddhist schools Pre-sectarian Buddh...

Spanish footballer In this Spanish name, the first or paternal surname is Corres and the second or maternal family name is Somovilla. Yulema Corres Corres in 2016Personal informationFull name Yulema Corres SomovillaDate of birth (1992-03-07) 7 March 1992 (age 32)[1]Place of birth Vitoria-Gasteiz, Spain[2]Height 1.70 m (5 ft 7 in)Position(s) ForwardYouth career CDF Gasteiz Cup[3]Senior career*Years Team Apps (Gls)2006–2014 Aurrera Vitoria 2...

City in Relizane Province, AlgeriaRelizane غليزانCityDowntownLocation of Taher in the Relizane ProvinceRelizaneLocation of Relizane in the AlgeriaCoordinates: 35°44′N 0°33′E / 35.733°N 0.550°E / 35.733; 0.550CountryAlgeriaProvinceRelizane ProvinceDistrictRelizane DistrictAPC2012-2017Government • TypeMunicipality • MayorOuagouag Medjaded (FLN)Area • Total110.82 km2 (42.79 sq mi)Elevation98 m (322 ...




























![{\displaystyle [\omega _{1},\omega _{2},\cdots \omega _{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed3b3323ee7dbc47be143f487b9885af758ef837)

![{\displaystyle P([\omega _{1},\omega _{2},\cdots ,\omega _{n}])=p^{k}(1-p)^{n-k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1eed2fcad96057c5a9acf5c2f4202ec8ede38a5)










![{\displaystyle \mathbb {E} [X_{i}]=\mathbb {P} ([X_{i}=1])=p,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32d3d5005d32d9b10eeea3256b89223da049917)


![{\displaystyle \mathbb {P} ([S_{n}=k])={n \choose k}p^{k}(1-p)^{n-k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/064d74a4f9259023631765cc878e2163345abc17)









