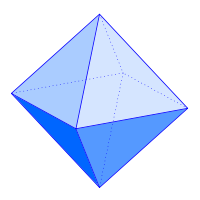
Pirámide cuadrada
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Lobak kubisKohlrabi stem with leavesSpesiesBrassica oleraceaKelompok budidayaGongylodes GroupAnggota kelompok kultivarMany; lihat teks. Kohlrabi, rawNilai nutrisi per 100 g (3,5 oz)Karbohidrat6.2 gGula2.6 gSerat pangan3.6 g Lemak0.1 g Protein1.7 g VitaminKuantitas %AKG†Vitamin A equiv.0% 2 μgTiamina (B1)4% 0.05 mgRiboflavin (B2)2% 0.02 mgNiasin (B3)3% 0.4 mgAsam pantotenat (B5)3% 0.165 mgVitamin B612% 0.15 mgFolat (B9)4% 16 μgVitamin B120% 0 μgVitamin C75% 62 mgVitamin D0%...

American judge (born 1954) For the composer, see Barry Anderson (composer). Barry AndersonAssociate Justice of the Minnesota Supreme CourtIncumbentAssumed office October 13, 2004 (2004-10-13)Appointed byTim PawlentyPreceded byJames H. GilbertJudge of the Minnesota Court of AppealsIn officeAugust 20, 1998 (1998-08-20) – August 27, 2004 (2004-08-27)Appointed byArne CarlsonSucceeded byChristopher Dietzen Personal detailsBornGrant Barry ...

MalumDesaPeta lokasi Desa MalumNegara IndonesiaProvinsiSumatera UtaraKabupatenPakpak BharatKecamatanSitellu Tali Urang JeheKode pos22272Kode Kemendagri12.15.01.2009 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Malum adalah salah satu desa di Kecamatan Sitellu Tali Urang Jehe, Kabupaten Pakpak Bharat, Provinsi Sumatera Utara, Indonesia. Legenda dan Sejarah Desa Sebelum Desa Malum dimekarkan pada tahun 2006 wilayah ini masih merupakan sebuah dusun. Ada dua dusun yang menjadi p...

Decoration for victorious generals of the Prussian Army and its allies The Grand Cross of the Iron Cross (German: Großkreuz des Eisernen Kreuzes) was a decoration intended for victorious generals of the Prussian Army and its allies. It was the second highest class of the Iron Cross, following the Star of the Grand Cross of the Iron Cross, which was awarded only twice. Along with the Iron Cross 1st and 2nd Class, the Grand Cross was founded on 10 March 1813, during the Napoleonic Wars. It was...

Koin Priapatius Priapatius (Persia: فریاپت /ˌfraɪəˈpeɪʃəs/) atau Phriapatius /ˌpraɪəˈpeɪʃəs/, terkadang disebut Phriapites /ˌfraɪˈæpɪtiːz/, merupakan seorang penguasa di Kekaisaran Parthia dari tahun 191 SM hingga 176 SM. Ia adalah putra dari seorang keponakan Arsaces I (bertakhta 247-217 SM), pendiri Kekaisaran Parthia. Sumber Junianus Justinus, xlv, 5. Schippmann, K. (1986b). Arsacids ii. The Arsacid dynasty. Encyclopaedia Iranica, Vol. II, Fasc. 5. hlm. 5...

Dalam nama yang mengikuti kebiasaan penamaan Slavia Timur ini, patronimiknya adalah Alekseyevna. Arina Averina— Pesenam —Arina Averina pada Kejuaraan Eropa 2017Informasi pribadiNama lengkapArina Alexeevna AverinaPanggilanTiger cubNegara RusiaLahir13 Agustus 1998 (umur 25)Zavolzhye, Oblast Nizhny NovgorodKlubCSKAPelatihIrina VinerAsisten pelatihVera ShatalinaMantan pelatihLarisa BelovaKoreograferIrina Zenovka, Tatiana Pomerantseva Arina Alekseyevna Averina (bahasa Rusia...

American politician Abraham G. LansingNew York State TreasurerIn office1810–1812GovernorDaniel D. TompkinsPreceded byDavid ThomasSucceeded byDavid ThomasIn office1803–1808GovernorGeorge ClintonMorgan LewisDaniel D. TompkinsPreceded byRobert McClellanSucceeded byDavid Thomas Personal detailsBornAbraham Gerritse Lansing(1756-12-12)December 12, 1756Albany, Province of New YorkDiedMay 15, 1834(1834-05-15) (aged 77)Albany, New YorkResting placeAlbany Rural CemeterySpouse Susanna Yates ...

First-level administrative divisions of Mauritania Politics of Mauritania Member State of the Arab League Constitution Human rights Slavery Government President Mohamed Ould Ghazouani Prime Minister Mohamed Ould Bilal Parliament National Assembly President Administrative divisions Regions Departments Communes Elections Recent elections Presidential: 201420192024 Parliamentary: 201320182023 Political parties Electoral districts Foreign relations Ministry of Foreign Affairs Minister: Ismail Oul...

Ceramic tile cutters are used to cut ceramic tiles to a required size or shape. They come in a number of different forms, from basic manual devices to complex attachments for power tools.[1] Hand tools Beam score cutters, cutter boards First Tile Cutter Invented by Boada Brothers The ceramic tile cutter works by first scratching a straight line across the surface of the tile with a hardened metal wheel and then applying pressure directly below the line and on each side of the line on ...

Berretti verdiJohn Wayne e George Takei in una scena del filmTitolo originaleThe Green Berets Paese di produzioneStati Uniti d'America Anno1968 Durata141 min Genereguerra RegiaJohn Wayne, Ray Kellogg SoggettoRobin Moore SceneggiaturaJohn Wayne, Ray Kellogg ProduttoreMichael Wayne, John Wayne FotografiaWinton C. Hoch MontaggioOtho Lovering MusicheMiklós Rózsa Interpreti e personaggi John Wayne: Col. Michael Mike Kirby David Janssen: George Beckworth Jim Hutton: sergente Petersen Aldo Ray: se...

Healin' Good PreCureSampul Volume pertama Blu-ray dari seri ini.ヒーリングっど♡プリキュア(Hīrin Guddo ♡ Purikyua)GenreMahou shōjo Seri animeSutradaraYoko IkedaProduserYasui KazunariSkenarioJunko KomuraMusikShiho TeradaStudioToei AnimationSaluranasliANN (ABC, TV Asahi)Tayang 2 Februari 2020 – 21 Februari 2021Episode45 (Daftar episode) MangaPengarangIzumi TodoIlustratorFutago KamikitaPenerbitKodanshaImprintWide KCMajalahNakayoshiDemografiShōjoTerbitMaret 2020 – sekarangVo...

College in Washington state, U.S. For the STA transit center, see Spokane Community College (Spokane Transit). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Spokane Community College – news · newspapers · books · scholar · JSTOR (November 2016) (Learn how and when to remove this message) Spokane Community ...

New Zealand politician (born 1971) The HonourableGrant RobertsonRobertson in 202310th Vice-Chancellor of the University of OtagoIncumbentAssumed office 1 July 2024ChancellorStephen HiggsPreceded byDavid Murdoch19th Deputy Prime Minister of New ZealandIn office6 November 2020 – 25 January 2023Prime MinisterJacinda ArdernPreceded byWinston PetersSucceeded byCarmel Sepuloni29th Minister of Foreign AffairsIn office11 November 2023 – 27 November 2023Prime Minister...

Óttar Magnús KarlssonNazionalità Islanda Altezza190 cm Calcio RuoloAttaccante Squadra Vis Pesaro CarrieraGiovanili Víkingur2013-2016 Ajax2016→ Sparta Rotterdam Squadre di club1 2013 Víkingur1 (0)2016 Víkingur20 (7)2017 Molde8 (0)2018→ Trelleborg14 (1)2019 Mjällby14 (1)2019-2020 Víkingur20 (14)2020-2021 Venezia7 (1)2021-2022→ Siena19 (2)2022-2023→ Oakland Roots32 (19)2023→ Virtus Francavilla7 (0)...
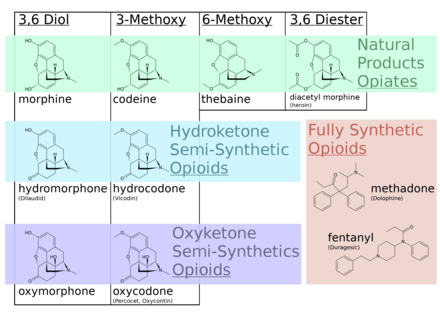
Substance derived from opium For the class of drugs, see Opioid. For other uses, see Opiate (disambiguation). Harvesting the poppy pod. A chart outlining the structural features that define opiates and opioids, including distinctions between semi-synthetic and fully synthetic opioid structures An opiate is an alkaloid substance derived from opium (or poppy straw).[1] It differs from the similar term opioid in that the latter is used to designate all substances, both natural and synthe...

レイモンド・メリル・スマリヤン 誕生 1919年5月25日ニューヨーク市死没 2017年2月6日職業 数学者、論理学者、哲学者、奇術師国籍 アメリカ合衆国 影響を受けたもの ルイス・キャロル ウィキポータル 文学テンプレートを表示 レイモンド・メリル・スマリヤン(Raymond Merrill Smullyan、1919年5月25日 - 2017年2月6日)は、アメリカ合衆国の数学者、ピアニスト、論理学者、老荘�...

American feminist writer and activist (1921–2006) Friedan redirects here. For the theoretical physicist, see Daniel Friedan. Betty FriedanFriedan in 1960BornBettye Naomi Goldstein(1921-02-04)February 4, 1921Peoria, Illinois, U.S.DiedFebruary 4, 2006(2006-02-04) (aged 85)Washington, D.C., U.S.Education Smith College (BA) University of California, Berkeley OccupationsWriteractivistNotable workThe Feminine Mystique (1963)Spouse Carl Friedan (m. 1947; di...

Le bureau Mazarin est un bureau associé au cardinal Mazarin, principal ministre de Louis XIV de 1642 à 1661. Cette forme de bureau est un ancêtre du bureau de ministre. Contrairement à ce dernier, le bureau Mazarin n'a pas de tiroirs descendant jusqu'au sol. Il possède des pieds reliés par des entretoises en « X » ou en « H »[1]. Plusieurs bureaux Mazarin ont été conçus pour être employés en angle, avec un genou sous la surface d'écriture et un autre genou...

دموع التماسيح (بالإنجليزية: Crocodile tears) أو التعاطف السطحي هو مصطلح يصف المشاعر الكاذبة تجاه شيء ما مثل إدعاء المنافق البكاء على حزن أو مصيبة وهو في الحقيقة لا يشعر بالحزن.[1] تستخدم التماسيح اسلوب النحيب والبكاء احياناً لكي تستدرج فريستها[بحاجة لمصدر] ومن هنا جاء وص�...

French writer and humorist Alphonse AllaisBornAlphonse AllaisHonfleur, Calvados, FranceDiedOctober 28, 1905(1905-10-28) (aged 51)[1]Paris, FrancePen nameFrancisque SarceyOccupationWriter, journalist[2]LanguageFrenchNationalityFrenchCitizenshipFranceAlphonse Allais (20 October 1854 in Honfleur – 28 October 1905 in Paris) was a French writer, journalist and humorist. He was also the editor of the Chat Noir, a satirical magazine. [3] Work He is the author of many c...