Operador escalera
|
Read other articles:

Immondizia non raccolta su una spiaggia a Napoli nel 2010, durante la crisi dei rifiuti. La crisi dei rifiuti in Campania indica lo stato di emergenza relativo allo smaltimento ordinario dei rifiuti solidi urbani (RSU) verificatosi in Campania dal 1994 al 2012.[1] Indice 1 Storia 1.1 Istituzione del Commissariato 1.2 Cambio di gestione 1.3 L'appalto per lo smaltimento dei rifiuti 1.4 La crisi della raccolta 1.5 Il biennio 2007-2008 1.6 La cessazione dello stato di emergenza e la fine ...

Peter Lorre (26 Juni 1904-23 Maret 1964), lahir László Loewenstein merupakan seorang aktor berkebangsaan Amerika Serikat-Austria. Dia dilahirkan di Ruzomberok, Austria-Hungaria. Dia berkarier di dunia film sejak tahun 1932 hingga wafat tahun 1964 di Los Angeles. Filmografi Die Verschwundene Frau M (1931) Bomben auf Monte Carlo Die Koffer des Herrn O.F. Fünf von der Jazzband F.P.1 antwortet nicht Der Weisse Dämon Stupéfiants Schuss im Morgengrauen Was Frauen träumen Unsichtbare Gegner Le...

Chin Wang (親王)Mijiddorjiin KhanddorjМижиддоржийн Ханддорж Menteri Urusan Luar NegeriMasa jabatan1911–1913Penguasa monarkiBodg Gegeen ke-8 Jebtsundamba Khutuktu PenggantiBalingiin Tserendorj Informasi pribadiLahir1869Meninggal1915Sunting kotak info • L • B Dalam artikel ini, nama keluarganya adalah Khanddorj. Rumah Khanddorj di Ulaanbaatar - sebuah campuran dari pengaruh Rusia dan Tionghoa Mijiddorjiin Khanddorj (Mongolian: Мижиддоржийн Ха�...

Philosophical system Not to be confused with Modern Platonism. Part of a series onNeoplatonismReconstructed bust believed to represent Plotinus Concepts Theory of forms Form of the Good Hypostasis Arche Nous Demiurge Logos Anima mundi Henosis Theurgy Okhema Microcosm and macrocosm Works Enneads De Mysteriis Aegyptiorum Liber de Causis The City of God The Consolation of Philosophy De Coelesti Hierarchia De divisione naturae Chaldean Oracles People Plotinus (students) Porphyry Iamblichus J...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Eighth GradePoster film Eighth GradeSutradaraBo BurnhamProduserScott RudinEli BushChristopher StorerLila YacoubDitulis olehBo BurnhamPemeranElsie FisherJosh HamiltonEmily RobinsonJake RyanFred HechingerPenata musikAnna MeredithSinematograferAndrew WehdePenyuntingJennifer LillyPerusahaanproduksiA24IAC FilmsScott Rudin ProductionsDistributorA24(Amerika Serikat)Sony Pictures(internasional)Tanggal rilis 19 Januari 2018 (2018-01-19) (Festival Film Sundance) 13 Juli 2018 (2018-0...

Officer rank of the United States Navy and Coast Guard Future ADM Michelle Howard when she was a U.S. Navy RDML on the USS Wasp (LHD-1) in 2009. A rear admiral in the uniformed services of the United States is either of two different ranks of commissioned officers: one-star flag officers and two-star flag officers. By contrast, in most other countries, the term rear admiral refers only to an officer of two-star rank. Rear admiral (lower half) For the Navy's previous one-star rank, see Commodo...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...

Азиатский барсук Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мле�...

American politician For other people named Henry Dixon, see Henry Dixon (disambiguation). Henry Aldous DixonMember of the U.S. House of Representativesfrom Utah's 1st districtIn officeJanuary 3, 1955 – January 3, 1961Preceded byDouglas R. StringfellowSucceeded byM. Blaine Peterson Personal detailsBornHenry Aldous Dixon(1890-06-29)June 29, 1890Provo, Utah TerritoryDiedJanuary 22, 1967(1967-01-22) (aged 76)Ogden, UtahResting placeWashington Heights Memorial ParkPolit...

English rock band This article is about the band. For other uses, see Police (disambiguation). The PoliceAndy Summers (far right), Sting (front), Stewart Copeland (drums). The Police performing at Madison Square Garden on 1 August 2007.Background informationOriginLondon, EnglandGenres New wave reggae rock post-punk pop rock Discography Albums and singles songs Years active 1977–1986 1992 2003 2007–2008 Labels Illegal A&M SpinoffsAnimal LogicOysterheadGizmodromeSpinoff ofCurved AirLast...
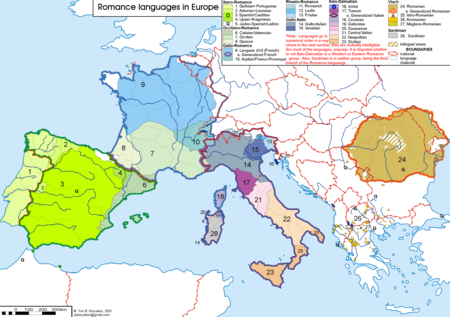
This template was considered for deletion on 2020 May 30. The result of the discussion was Keep seperate. Languages Template‑class Language portalThis template is within the scope of WikiProject Languages, a collaborative effort to improve the coverage of languages on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.LanguagesWikipedia:WikiProject LanguagesTemplate:WikiProject Languageslanguage articles...

Alphanumeric code specifying tire sizes and limits Assorted new car tires with a variety of tread patterns and different sizes Automotive tires are described by an alphanumeric tire code (in North American English) or tyre code (in Commonwealth English), which is generally molded into the sidewall of the tire. This code specifies the dimensions of the tire, and some of its key limitations, such as load-bearing ability, and maximum speed. Sometimes the inner sidewall contains information not i...

American historian and writer Dumas MaloneBorn10 January 1892Coldwater, Mississippi, U.S.Died27 December 1986 (aged 94)Charlottesville, Virginia, U.S.EducationEmory College (BA)Yale University (BDiv, MA, PhD)Notable workJefferson and His TimeSpouse Elizabeth Gifford (m. 1925)RelativesKemp Malone (brother)AwardsPulitzer Prize for History (1975)Presidential Medal of Freedom (1983)Signature Dumas Malone (DEW-mah;[1] January 10, 1892 – December 27, 1986) w...

2002 single by the X-Ecutioners featuring Mike Shinoda and Mr. HahnIt's Goin' DownSingle by the X-Ecutioners featuring Mike Shinoda and Mr. Hahnfrom the album Built from Scratch Released11 March 2002Recorded2001Genre Nu metal[1] rap rock[2] Length 4:08 (album version) 3:32 (radio version) Label Loud Columbia Songwriter(s) Mike Shinoda Joe Hahn Melvin Bradford Alvin Joiner Producer(s)Mike ShinodaThe X-Ecutioners singles chronology Música Negra (Black Music)/Wordplay (1997)...

Triumphal arch in Berlin, Germany This article is about the gate in Berlin. For other uses, see Brandenburg Gate (disambiguation). Brandenburg GateBrandenburger TorView from the Pariser Platz on the east sideGeneral informationTypeCity gateArchitectural styleNeoclassicalLocationBerlin, GermanyCoordinates52°30′59″N 13°22′40″E / 52.5163°N 13.3777°E / 52.5163; 13.3777Construction started1788Completed1791Design and constructionArchitect(s)Carl Gotthard Langhans...

Law prohibiting tobacco smoking in a given space Smoking bans redirects here. For a list, see List of smoking bans. An internationally recognizable no smoking sign An internationally recognizable black authorization to smoke sign Smoking bans, or smoke-free laws, are public policies, including criminal laws and occupational safety and health regulations, that prohibit tobacco smoking in certain spaces. The spaces most commonly affected by smoking bans are indoor workplaces and buildings open ...

中華人民共和国の政治家李嵐清生年月日 (1932-05-22) 1932年5月22日(92歳)出生地 中華民国、江蘇省鎮江県出身校 復旦大学企業管理学科所属政党 中国共産党配偶者 章素貞 中央政治局常務委員会委員在任期間 1997年9月18日 - 2002年11月7日党総書記 江沢民 国務院常務副総理内閣 朱鎔基内閣在任期間 1998年3月 - 2003年3月国家主席 江沢民 国務院副総理内閣 李鵬内閣在任期間 1993�...

This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2023) Low table meant to be placed in sitting areas This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Coffee table – news · newspapers · books · scholar · JSTOR (November 2019) (...

For the song by The Beastie Boys, see Hot Sauce Committee Part Two. 1972 studio album by Black MerdaLong Burn the FireStudio album by Black MerdaReleased1972Genre Acid rock psychedelic soul funk rock blues rock Length34:17LabelJanus RecordsBlack Merda chronology Black Merda(1970) Long Burn the Fire(1972) The Folks from Mother's Mixer(2005) Professional ratingsReview scoresSourceRatingChristgau's Record GuideB+[1] Long Burn the Fire is the second studio album by the Detroit roc...


![{\displaystyle [{\hat {N}},{\hat {X}}]=c{\hat {X}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bddb22e32309b6a771e93edc6bb002b85e540cbc)


![{\displaystyle {}=({\hat {X}}{\hat {N}}+[{\hat {N}},{\hat {X}}])|n\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a7602e41eba1aaa9c2e1fedfa895234661c9267)









![{\displaystyle [{\hat {N}},{\hat {X}}^{\dagger }]=-c{\hat {X}}^{\dagger }.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/102a73295f1283f198192d22e360d0d82a5f8aeb)













![{\displaystyle \left[{\hat {X}},{\hat {P}}\right]=i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dde94b2c9d03c1ef0ba18373c4b6c3d2e6c1dab8)
![{\displaystyle \left[a,a^{\dagger }\right]={\hat {a}}{\hat {a}}^{\dagger }-{\hat {a}}^{\dagger }{\hat {a}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc4ab67dfa6c05602c7b6b4e8d08a13d4cf76e4f)





![{\displaystyle [{\hat {N}},{\hat {a}}]={\hat {N}}{\hat {a}}-{\hat {a}}{\hat {N}}={\hat {a}}^{\dagger }{\hat {a}}{\hat {a}}-{\hat {a}}{\hat {a}}^{\dagger }{\hat {a}}=-{\hat {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/941bc482522a0959f0f160202ae5bdb3dc5c35df)


































![{\displaystyle [{\hat {a}}_{\mathbf {k} },{\hat {a}}_{\mathbf {k'} }^{\dagger }]=\delta ^{(3)}(\mathbf {k} -\mathbf {k'} ),\quad [{\hat {a}}_{\mathbf {k} },{\hat {a}}_{\mathbf {k'} }]=0,\quad [{\hat {a}}_{\mathbf {k} }^{\dagger },{\hat {a}}_{\mathbf {k'} }^{\dagger }]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd79e620609d581237510fe4033ddc6b4080710)