Número perfecto múltiple
|
Read other articles:

Pub in the City of London Simpson's Tavern, London Simpson's Tavern is or was a pub and restaurant at 38 1/2, Ball Court Alley, Cornhill, in the City of London, EC3. Simpson's Tavern's sign at the entrance of Ball Court Simpson's occupied a Grade II listed building, built in the late 17th and early 18th centuries.[1] Simpson's Tavern was closed down by the owner of the building on 28 October 2022, following a dispute about rental payments.[2][3] Image records 1812 Reco...

Tim HealyHealy, c. 1915 Gubernur Jenderal Negara Bebas Irlandia Ke-1Masa jabatan6 Desember 1922 – 31 Januari 1928Penguasa monarkiGeorge V PendahuluJabatan dibentukPenggantiJames McNeillAnggota ParlemenMasa jabatan1880–1918 Informasi pribadiLahir(1855-05-17)17 Mei 1855Bantry, County Cork, IrlandiaMeninggal26 Maret 1931(1931-03-26) (umur 75)Chapelizod, County Dublin, IrlandiaSuami/istriErina Sullivan (m. 1882, d. 1927)ProfesiPoliticianSunting kotak info • L • B T...

SeriesPegasus CrimeSubjectPopular Fiction-Contemporary ThrillersGenreCrimePublisherHarperCollinsPublication date2008Pages480 pagesISBN0-00-741951-1Preceded byThe Hidden Child Followed byThe_Lost_Boy_(novel) The Drowning is a 2008 novel by Camilla Läckberg. Its Swedish title is Sjöjungfrun, literally translated in English as The Mermaid. Like Margaret Atwood's The Blind Assassin, The Drowning contains a novel within a novel: 'The Mermaid' is that story.[1] Refere...

العلاقات الدومينيكية اللبنانية دومينيكا لبنان دومينيكا لبنان تعديل مصدري - تعديل العلاقات الدومينيكية اللبنانية هي العلاقات الثنائية التي تجمع بين دومينيكا ولبنان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ا...

Placozoa TaksonomiSuperkerajaanEukaryotaKerajaanAnimaliaFilumPlacozoa Grell, 1971 Tipe taksonomiTrichoplax adhaerens FamiliTrichoplacidaelbs Placozoa adalah filum hewan invertebrata yang memiliki struktur paling sederhana dari semua hewan. Mereka umumnya diklasifikasikan sebagai spesies tunggal, Trichoplax adhaerens, meskipun ada keragaman genetik yang cukup sehingga mungkin ada lebih dari satu spesies dengan morfologi yang sama.[1][2] Placozoa pertama kali ditemukan pada tahu...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Nature preserve in California, United States Blue Ridge National Wildlife RefugeIUCN category IV (habitat/species management area)Map of the United StatesLocationTulare County, California, United StatesNearest citySpringville, CaliforniaCoordinates36°16′47″N 118°50′41″W / 36.2798°N 118.8446°W / 36.2798; -118.8446[1]Area897 acres (3.63 km2)Established1982Governing bodyU.S. Fish and Wildlife ServiceWebsiteBlue Ridge National Wildlife Re...
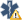
متلازمة الغدد الصماء بالمناعة الذاتية معلومات عامة الاختصاص علم الغدد الصم من أنواع مرض مناعي ذاتي في الغدد الصماء [لغات أخرى]، ومرض تعديل مصدري - تعديل في مجال الطب، تُعد متلازمات المناعة الذاتية ضد الغدد الصماء المتعددة، وتُسمَّى أيضًا بـمتلازمة ...

Carle Vernet; potret karya Robert Lefevre Antoine Charles Horace Vernet alias Carle Vernet atau Charlot (14 Agustus 1758 – 17 November 1836) adalah seorang pelukis asal Prancis. Ia adalah anak bungsu dari seorang pelukis lanskap Claude Joseph Vernet, dan ayah dari Horace Vernet.[1] Ia pernah melukis pertempuran Napoleon I dan melukiskan subjek-subjek olahraga, terutama kuda, untuk Raja Louis XVIII.[2] Biografi The Pertempuran Wagram; dilukis oleh Carle Vernet d...

Grand Prince of Tuscany Ferdinando de' MediciGrand Prince of TuscanyBorn(1663-08-09)9 August 1663Palazzo Pitti, Florence, TuscanyDied31 October 1713(1713-10-31) (aged 50)Palazzo Pitti, Florence, TuscanyBurialBasilica of San Lorenzo, FlorenceSpouseViolante Beatrice of BavariaNamesFerdinando de' MediciHouseMediciFatherCosimo III, Grand Duke of TuscanyMotherMarguerite Louise d'Orléans Ferdinando de' Medici (9 August 1663 – 31 October 1713) was the eldest son of Cosimo III de' Medici, Gr...

Turkish economic crisis redirects here. See also 2001 Turkish economic crisis. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) Parts of this article (those related to events from 2022 and 2023) need to be updated. Please help update this article to reflect recent events or newly available information. (January 2023) This article may contain an excessive amount of intricate detail that ma...

Australian architect (1919-1971) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Robin Boyd architect – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this message) Robin BoydCBEBoyd's Hilary Roche House (1954) in Deakin, ACT, is typical of the post-war Melbou...

İlnur ZäkärinIlnur Zakarin avec le maillot jaune du Tour de Romandie 2015InformationsNom court Ильнур ЗакаринNaissance 15 septembre 1989 (34 ans)Naberejnye TchelnyNationalité russeSpécialité courses à étapes[1]Équipes UCI 2012-7.2012Itera-Katusha8.2012-2012Katusha (stagiaire)2013-2014RusVelo2015-2016Katusha2017-2019Katusha-Alpecin2020CCC Team2021-6.2022Gazprom-RusVeloPrincipales victoires Championnats Champion d'Europe du contre-la-montre juniors 2007 Champion de Ru...

Come leggere il tassoboxFalco pellegrinoFalco peregrinusStato di conservazioneRischio minimo[1] Classificazione scientificaDominioEukaryota RegnoAnimalia SottoregnoEumetazoa SuperphylumDeuterostomia PhylumChordata SubphylumVertebrata SuperclasseTetrapoda ClasseAves SottoclasseNeornithes SuperordineNeognathae OrdineFalconiformes FamigliaFalconidae SottofamigliaFalconinae GenereFalco SpecieF. peregrinus Nomenclatura binomialeFalco peregrinusTunstall, 1771 Areale &...

Cet article est une ébauche concernant l’art et une chronologie ou une date. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Données clés 1819 1820 1821 1822 1823 1824 1825Décennies :1790 1800 1810 1820 1830 1840 1850Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du S...

Swedish linguist (1894–1983) Björn CollinderBorn(1894-07-22)22 July 1894Sundsvall, SwedenDied20 May 1983(1983-05-20) (aged 88)Vienna, AustriaNationalitySwedishAcademic backgroundAlma mater Uppsala University Academic advisorsK. B. WiklundAcademic workDisciplineLinguisticsInstitutions Uppsala University Notable students Bo Wickman Main interestsFinno-Ugric languages Erik Alfred Torbjörn Björn Collinder (22 July 1894 – 20 May 1983) was a Swedish linguist who was Professor of Finno-U...

Abelardo L. Rodríguez Rodríguez en 1932 Presidente de los Estados Unidos MexicanosSustituto 2 de septiembre de 1932-30 de noviembre de 1934Designado por Congreso de la UniónGabinete Gabinete de Abelardo L. RodríguezPredecesor Pascual Ortiz RubioSucesor Lázaro Cárdenas Gobernador de Sonora 13 de septiembre de 1943-15 de abril de 1948Predecesor Anselmo Macías ValenzuelaSucesor Horacio Sobarzo Díaz Secretario de Industria, Comercio y Trabajo 20 de enero de 1932-2 de septiembre de 1932Pre...

1923 film The Call of the CanyonLobby cardDirected byVictor FlemingScreenplay by Edfrid A. Bingham Doris Schroeder Based onThe Call of the Canyonby Zane GreyProduced byJesse LaskyStarring Richard Dix Lois Wilson Marjorie Daw CinematographyJames Wong HoweProductioncompanyFamous Players–LaskyDistributed byParamount PicturesRelease date December 16, 1923 (1923-12-16) (USA) Running time70 minutes7 reels, 6,993 ftCountryUnited StatesLanguageSilent (English intertitles) The Cal...

Questa voce sull'argomento calciatori brasiliani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. RodneiNazionalità Brasile Altezza190 cm Peso91 kg Calcio RuoloDifensore Termine carriera2022 CarrieraGiovanili Juventus-SP Squadre di club1 2005-2006 Juventus-SP? (?)2006-2007 Vilnius46 (7)2007 Pão de Açúcar? (?)2007-2008→ Jagiellonia11 (0)2008-2009 Hertha Berlino9...

Watchmen character For the band, see Dr Manhattan (band). For the album, see Dr Manhattan (album). Comics character Doctor ManhattanArt by Dave GibbonsPublication informationPublisherDC ComicsFirst appearanceWatchmen #1 (September 1986)Created byAlan MooreDave GibbonsIn-story informationAlter egoDr. Jonathan Jon OstermanCalvin Cal Abar (né Jelani)Team affiliationsUnited States Department of DefensePartnershipsRomantic partners:Janey SlaterLaurie JuspeczykAngela AbarChildren:Christopher Tophe...








![{\displaystyle r\left({\sqrt[{r}]{3/2}}-1\right)<\sum _{i=1}^{r}{\frac {1}{p_{i}}}<r\left(1-{\sqrt[{r}]{6/k^{2}}}\right),~~{\text{si }}n{\text{ es par}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0be76057c34d9bd66ff4937c9f14ee115e020c1)
![{\displaystyle r\left({\sqrt[{3r}]{k^{2}}}-1\right)<\sum _{i=1}^{r}{\frac {1}{p_{i}}}<r\left(1-{\sqrt[{r}]{8/(k\pi ^{2})}}\right),~~{\text{si }}n{\text{ es impar}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03f05d88054afb918e307014464cadb26d3f5acb)