Número de Dottie

En matemática, el número de Dottie es una constante que es la única raíz real de la ecuación

\cos x=x,

donde el argumento del $\cos$ está expresado en radianes. La expansión decimal del número de Dottie es $0.739085...$ .^[1]

Se puede demostrar trivialmente que la ecuación solo tiene una solución en el dominio real mediante el teorema del valor intermedio. Es el punto fijo simple de valor real de la función coseno, y es un ejemplo no trivial de un punto fijo de un atractor universal. Más aún, es un número trascendental y es consecuencia del teorema de Lindemann-Weierstrass.^[2] El caso más general $\cos z=z$ para la variable compleja $z$ tiene infinitas raíces, sin embargo, a diferencia del número de Dottie esas soluciones no son puntos fijos de atractor. Usando la serie de Taylor de la inversa de $f(x)=\cos(x)-x$ en ${\frac {\pi }{2}}$ (o equivalentemente, el teorema de inversión de Lagrange), el número de Dottie se puede expresar como una serie infinita ${\frac {\pi }{2}}+\sum _{n\,\mathrm {impar} }a_{n}\pi ^{n}$ donde cada $a_{n}$ es un número racional definido para los impares n como

{\begin{aligned}a_{n}&={\frac {1}{n!2^{n}}}\lim _{m\to {\frac {\pi }{2}}}{\frac {\partial ^{n-1}}{\partial m^{n-1}}}{\left({\frac {\cos m}{m-\pi /2}}-1\right)^{-n}}\\&=-{\frac {1}{4}},-{\frac {1}{768}},-{\frac {1}{61440}},-{\frac {43}{165150720}},\ldots \end{aligned}}

^[3]^[4]^[5]^{[nb 1]}

El nombre de la constante viene originado por Samuel Kaplan (2007) y se refiere a una profesora de francés, la cual observó el número después de presionar repetidamente el botón coseno de su calculadora.^[3]

Notas

↑ Kaplan no da una forma explícita para los términos de la serie pero se puede deducir trivialmente del teorema de inversión de Lagrange

Referencias

↑ «OEIS A003957». oeis.org. Consultado el 26 de mayo de 2019.
↑ Eric W. Weisstein. «Dottie Number».
↑ ^a ^b Kaplan, Samuel R (February 2007). «The Dottie Number». Mathematics Magazine 80: 73. doi:10.1080/0025570X.2007.11953455. Consultado el 29 de noviembre de 2017.
↑ «OEIS A302977 Numerators of the rational factor of Kaplan's series for the Dottie number.». oeis.org. Consultado el 26 de mayo de 2019.
↑ «A306254 - OEIS». oeis.org. Consultado el 22 de julio de 2019.

Datos: Q48996451

Enlaces externos

Miller, T. H. (Feb 1890). «On the numerical values of the roots of the equation cosx = x». Proceedings of the Edinburgh Mathematical Society 9: 80-83. doi:10.1017/S0013091500030868.
Salov, Valerii (2012). «Inevitable Dottie Number. Iterals of cosine and sine». arXiv:1212.1027.
Azarian, Mohammad K. (2008). «ON THE FIXED POINTS OF A FUNCTION AND THE FIXED POINTS OF ITS COMPOSITE FUNCTIONS». International Journal of Pure and Applied Mathematics.

Read other articles:

Ore, Tsushima

Ore, TsushimaBerkas:Ore, Tsushima volume 1 cover.jpgCover of Ore, Tsushima volume 1 by Shogakukan俺、つしま MangaPengarangOpūnokyōdaiPenerbitShogakukanDemografiSeinenTerbitJuly 2017 – sekarangVolume3 Seri animeSutradaraJun AokiStudioFanworksSpace Neko CompanyPelisensiSA / SEA Muse CommunicationSaluranasliMBS, TBS, BS-TBSTayang July 3, 2021 – September 18, 2021Episode12 Animasi web orisinalSutradaraYoshitomoMusikSatoshi HounoStudioAQUA ARISPelisensiSA / SEA Muse CommunicationT...

Gereja Sant'Ignazio, Roma

Gereja Sant'IgnazioGereja Santo Ignatius dari Loyola di Campus MartiusItalia: Chiesa di Sant'Ignazio di Loyola in Campo Marziocode: it is deprecated Latin: Ecclesia Sancti Ignatii a Loyola in Campo Martiocode: la is deprecated Fasad Sant'Ignazio41°53′56.4″N 12°28′47.2″E / 41.899000°N 12.479778°E / 41.899000; 12.479778Koordinat: 41°53′56.4″N 12°28′47.2″E / 41.899000°N 12.479778°E / 41.899000; 12.479778LokasiVia del Caravit...

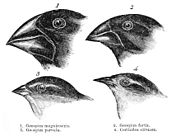
Ecological genetics

Study of genetics in natural populations Ecological Genetics redirects here. For the book by E. B. Ford, see Ecological Genetics (book). Part of a series onEvolutionary biologyDarwin's finches by John Gould Index Introduction Main Outline Glossary Evidence History Processes and outcomes Population genetics Variation Diversity Mutation Natural selection Adaptation Polymorphism Genetic drift Gene flow Speciation Adaptive radiation Co-operation Coevolution Coextinction Divergence Convergence Par...

Jintan hitam

Untuk kegunaan lain, lihat Jintan (disambiguasi). Jintan hitam Nigella sativa TumbuhanJenis buahFolikel TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsOrdoRanunculalesFamiliRanunculaceaeSubfamiliRanunculoideaeTribusNigelleaeGenusNigellaSpesiesNigella sativa Linnaeus, 1753 lbs Nigella sativa Jintan hitam (Nigella sativa) adalah terna, daunnya berbau segar, bijinya mengandung minyak asiri dan lemak, digunakan untuk rempah-rempah dan campuran...

Pembagian administratif Dominika

Peta pembagian administratif tingkat pertama Dominika Pembagian administratif Dominika terdiri atas 10 paroki pada tingkat pertama. Tingkat pertama Saint Andrew Saint David Saint George Saint John Saint Joseph Saint Luke Saint Mark Saint Patrick Saint Paul Saint Peter lbsPembagian administratif Amerika Amerika Utara Amerika Selatan Negara berdaulat Amerika Serikat Antigua dan Barbuda Argentina Bahama Barbados Belize Bolivia Brasil Chili Dominica Republik Dominika Ekuador El Salvador Grenada G...

Interpublic Group of Companies

The Interpublic Group of Companies, Inc.JenisPublikKode emitenNYSE: IPGKomponen S&P 500IndustriAgen periklananPendahuluMcCann-Erickson, Inc.Didirikan1930; 94 tahun lalu (1930) (dengan nama McCann Erickson)1961 (1961) (dengan nama Interpublic Group)KantorpusatThird Avenue no. 909New York City, New York 10022Amerika SerikatTokohkunciMichael I. Roth, Chairman, CEO, & Presiden[1]Pendapatan US$9,71 milyar[2] (2018)Laba operasi US$1,01 milyar[2&#...

Daftar distrik, kelurahan, dan kampung di Papua Tengah

Peta Provinsi Papua Tengah di Indonesia Berikut adalah daftar distrik/kecamatan dan kelurahan di Provinsi Papua Tengah, Indonesia. Provinsi Papua Tengah terdiri dari 8 kabupaten, 130 distrik, 36 kelurahan, dan 1.172 kampung. Pada tahun 2017, jumlah penduduknya diperkirakan mencapai 1.177.902 jiwa dengan total luas wilayah 61.012,18 km².[1][2] No. Kode Kemendagri Kabupaten/Kota Ibukota Luas Wilayah (km2) Penduduk (jiwa) 2017 Distrik Kelurahan Kampung 1 91.28 Kab. Deiyai Tigi 5...

Price elasticity of demand

Sensitivity of quantity to price Elasticity of demand redirects here. For income elasticity, see Income elasticity of demand. For cross elasticity, see Cross elasticity of demand. For wealth elasticity, see Wealth elasticity of demand. Price elasticity redirects here. Not to be confused with Price elasticity of supply. A good's price elasticity of demand ( E d {\displaystyle E_{d}} , PED) is a measure of how sensitive the quantity demanded is to its price. When the price rises, quantity deman...

Hyundai Lavita

Not to be confused with Toyota Matrix. Motor vehicle Hyundai Lavita (FC)Pre-facelift Hyundai Elantra LaVita (Australia)OverviewManufacturerHyundaiAlso calledHyundai Matrix (Europe, ASEAN and Israel)Hyundai Elantra LaVita (Australia)Inokom Matrix (Malaysia)Production2001–2007 (South Korea)2007–2010 (Turkey)AssemblyUlsan, South Korea[1]İzmit, Turkey (Hyundai Assan)[2]Kulim, Malaysia (Inokom)Cairo, Egypt (Ghabbour Group)Athens, Greece (Hyundai Hellas AEBE)DesignerLorenz...

Siamraptor

Extinct genus of dinosaurs SiamraptorTemporal range: Aptian~120–112 Ma PreꞒ Ꞓ O S D C P T J K Pg N Skeletal reconstruction and size comparison of Siamraptor suwati Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Theropoda Clade: †Allosauria Clade: †Carcharodontosauria Genus: †SiamraptorChokchaloemwong et al., 2019 Species: †S. suwati Binomial name †Siamraptor suwatiChokchaloemwong et al...

Milan Associazione Sportiva 1936-1937

Voce principale: Associazione Calcio Milan. Milan ASStagione 1936-1937 Sport calcio Squadra Milan Allenatore Adolfo Baloncieri[1], poi William Garbutt[2] PresidenteConsiglio di reggenza[3], poi Emilio Colombo[4] Serie A4º Coppa ItaliaSemifinalista Maggiori presenzeCampionato: Bonizzoni, Bortoletti e Perversi (30)Totale: Bonizzoni, Bortoletti e Perversi (36) Miglior marcatoreCampionato: Capra (12)Totale: Boffi (15) StadioSan Siro 1935-1936 1937-1938 Si in...

淡江高峰塔倒塌事件

淡江高峰塔倒塌事件高峰塔B座、C座公寓，與倒塌的A座公寓結構類似 (2012)日期1993年12月11日，30年前（1993-12-11）时间下午1时35分（马来西亚标准时间，周六）地点马来西亚雪兰莪淡江（英语：Ulu Klang）山景花园（英语：Taman Hillview）高峰塔坐标3°10′33.4″N 101°45′42.1″E / 3.175944°N 101.761694°E / 3.175944; 101.761694坐标：3°10′33.4″N 101°45′42.1″E&...

List of current senators of Canada

The Senate Chamber, located in the Centre Block of Parliament Hill This is a list of current members of the Senate of Canada (French: Le Sénat du Canada), the upper house of the Parliament of Canada. Unlike the members of Parliament in the House of Commons, the 105 senators are appointed by the governor general on the advice of the prime minister.[1] Senators originally held their seats for life; however, under the British North America Act, 1965, members may not sit in the Senate a...

Corregimientos of Panama

Administrative territorial entity of Panama This article needs to be updated. The reason given is: missing Naso Tjër Di Comarca, created in 2020. Please help update this article to reflect recent events or newly available information. (February 2022) Politics of Panama Constitution Abortion law LGBT rights Executive President Laurentino Cortizo Vice President Jose Gabriel Carrizo Legislature National Assembly President: Marcos Castillero Barahona Administrative divisions Provinces and comarc...

Lorraine Regional Natural Park

Regional natural park of France Lorraine Regional Natural ParkParc naturel régional de LorraineIUCN category V (protected landscape/seascape)The Côtes de Meuse, viewed from the Butte de MontsecLocation in FranceLocationDepartments of MeuseMeurthe-et-MoselleMoselle, Grand Est Region, FranceCoordinates48°53′23″N 6°02′39″E / 48.88967°N 6.04428°E / 48.88967; 6.04428Area205,000 ha (790 sq mi)Governing bodyFédération des parcs naturels ré...

Jalan Tol Medan—Kualanamu—Tebing Tinggi

Jalan Tol Medan—Kualanamu—Tebing Tinggi (MKTT)Informasi ruteDikelola oleh PT Jasa Marga Kualanamu Tol (JMKT)Panjang:61.80 km (38,40 mi)Berdiri:13 Oktober 2017 – sekarangPersimpangan besarUjung Selatan:Jalan Tol Kuala Tanjung-Tebing Tinggi-Parapat Simpang SusunTebing Tinggi JunctionSimpang Susun Sei RampahSimpang Susun Teluk MengkuduSimpang Susun PerbaunganSimpang Susun Lubuk PakamSimpang Susun KemiriSimpang Susun Kualanamu JunctionSimpang Susun Perbarakan Junction Simpang...

المعبودات المصرية القديمة

جزء من سلسلة مقالات حولديانة قدماء المصريين مفاهيم الحياة الآخرة دوات ماعت الأساطير الأرقام الفلسفة الروح طقوس الجنائزية القرابين المعابد الأهرامات الآلهةثامون هيرموبوليس (أجدود) آمون أمونيت حح ححيت ككوي ككويت نوو نوونيت تاسوع هليوبوليس أتوم جب إيزيس نيفتيس نوت أوزيريس...

Mangatainoka (rivière)

rivière Mangatainokaanglais : Mangatainoka River Vue de la rivière Mangatainoko Seventy Mile Bush , N.Z. Mangatainoka River sur OpenStreetMap. Caractéristiques Longueur 17 km [note 1] Cours Source côté Est de la chaîne de Tararua · Coordonnées 39° 07′ 43″ S, 176° 15′ 33″ E Confluence rivière Tiraumea · Coordonnées 39° 09′ 45″ S, 176° 23′ 43″ E Géographie Pays traversés Nouvelle-Zélande Îl...

M'zab

For other uses, see Mzab. UNESCO World Heritage Site in Ghardaïa Province, Algeria M'Zab ValleyUNESCO World Heritage SitePanoramic view of Ghardaïa (Tagherdayt) with the dry bed of Wadi M'zab on the right sideLocationGhardaïa Province, AlgeriaCriteriaCultural: (ii), (iii), (v)Reference188Inscription1982 (6th Session)Area665.03 ha (1,643.3 acres)Websitewww.opvm.dzCoordinates32°29′N 3°41′E / 32.483°N 3.683°E / 32.483; 3.683Location of M'zab in Al...

Unione Sportiva Salernitana 1976-1977

Voce principale: Unione Sportiva Salernitana 1919. Unione Sportiva SalernitanaStagione 1976-1977 Sport calcio Squadra Salernitana Allenatore Carlo Regalia(fino al 10/04/1977) Mario Saracino[1](dal 10/04/1977) All. in seconda Mario Saracino Presidente Pietro Esposito(fino al 24/11/1976) Aldo Matera(dal 24/11/1976) Serie C6º posto Coppa Italia SemiprofessionistiOttavi di finale Maggiori presenzeCampionato: Marinelli, Onor (35) Miglior marcatoreCampionato: Mujesan (12)Totale: Muje...