Modelo Beverton–Holt
|
Read other articles:

Achmad Wibisono Asisten Perencanaan dan Anggaran KasalPetahanaMulai menjabat 21 Februari 2024 PendahuluEdwinPenggantiPetahanaPanglima Komando Armada IMasa jabatan17 Juli 2023 – 21 Februari 2024 PendahuluErwin S. AldedharmaPenggantiPetahanaKepala Staf Komando Gabungan Wilayah Pertahanan II ke-5Masa jabatan29 Maret 2023 – 17 Juli 2023 PendahuluAhmad Rizal RamdhaniPenggantiRudhi AviantaraKepala Staf Komando Gabungan Wilayah Pertahanan III ke-4Masa jabatan31 Janu...

في هذه المقالة ألفاظ تعظيم تمدح موضوع المقالة، وهذا مخالف لأسلوب الكتابة الموسوعية. فضلاً، أَزِل ألفاظ التفخيم واكتفِ بعرض الحقائق بصورة موضوعية ومجردة ودون انحياز. (نقاش)جزء من سلسلة مقالات حولالشيعة العقيدة توحيد الله الإيمان بالملائكة الإيمان بالكتب السماوية الإيمان ...

Nasihat Pertapa karya Behzad (s. 1500-1550). Seperti halnya naskah beriluminasi dunia Barat, bagian pinggir yang dihias merupakan bagian mendalam dari karya seni tersebut. Miniatur Persia adalah sebuah lukisan kecil di atas kertas, yang menjadi sebuah ilustrasi buku atau karya seni lepas yang disimpan dalam sebuah album yang berisi karya-karya semacam itu yang disebut muraqqa. Tekniknya sebanding dengan tradisi miniatur Barat dan Bizantium dalam naskah beriluminasi. Meskipun mirip dengan trad...

Society driven by the use of technology to enable mass production Chicago and Northwestern railroad locomotive shop in the 20th century In sociology, an industrial society is a society driven by the use of technology and machinery to enable mass production, supporting a large population with a high capacity for division of labour. Such a structure developed in the Western world in the period of time following the Industrial Revolution, and replaced the agrarian societies of the pre-modern, pr...

Edition of USA college basketball tournament 2013 NCAA Division Imen's basketball tournamentSeason2012–13Teams68Finals siteGeorgia DomeAtlanta, GeorgiaChampionsLouisville Cardinals (Vacated) (3rd title, 3rd title game, 10th Final Four)Runner-upMichigan Wolverines (6th title game,7th Final Four)SemifinalistsSyracuse Orange (5th Final Four)Wichita State Shockers (2nd Final Four)Winning coachRick Pitino* [a] (2nd title)MOPLuke Hancock (Louisville) NCAA Division I men's tournaments ...

Part of the advertising industry Marketing Marketing Marketing management Key concepts Distribution Pricing Retail Service Activation Brand licensing Brand management Co-creation Consumer behaviour Consumer culture Dominance Effectiveness Ethics Promotion Segmentation Strategy Account-based marketing Digital marketing Product marketing Social marketing Influencer marketing Attribution Annoyance factor Horizontal integration Vertical integration Promotional content Advertising Branding Corpora...

Serangan Taliban 2021Bagian dari Perang di Afganistan (2001–2021) dan Pemberontakan TalibanPeta Afganistan ini menampilkan wilayah serangan Taliban di akhir serangan pada 15 Agustus 2021.(Lihat peta terperinci mengenai situasi militer terkini di Afganistan.)Tanggal1 Mei 2021 – 15 Agustus 2021[7](3 bulan dan 2 minggu)LokasiAfganistanHasil Kemenangan Taliban; kejatuhan Republik Islam Afganistan Presiden Ashraf Ghani meninggalkan Afganistan[8][9][10]...

Maudy AyundaMaudy pada tahun 2019LahirAyunda Faza Maudya19 Desember 1994 (umur 29)Jakarta, IndonesiaAlmamater Universitas Oxford Universitas Stanford PekerjaanAktrismodelaktivispenulispenyanyi-penulis laguTahun aktif2005–sekarangSuami/istriJesse Choi (m. 2022)PenghargaanForbes Asia 30 Under 30, 2021Karier musikGenrePopR&BInstrumenVokalgitarpianoLabelTrinity OptimaArtis terkaitDavid ChoiDewi Lestari SimangunsongRida FaridaSita NursantiTeddy Adhit...

Brewery in Puerto Vallarta, Jalisco, Mexico Los Muertos BrewingExterior of the restaurant in Zona Romántica, 2023Restaurant informationEstablished2012 (2012)Owner(s)Conner WattsCityPuerto VallartaStateJaliscoCountryMexicoCoordinates20°36′13″N 105°14′06″W / 20.6036°N 105.2349°W / 20.6036; -105.2349 Los Muertos Brewing is a brewery and restaurant with two locations in Puerto Vallarta, in the Mexican state of Jalisco. There is one location on Lázaro Cá...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2016). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? C...

Japanese signal baton and war fan The gunbai (軍配, short for 軍配団扇 gunbai-uchiwa) is a type of signal baton and Japanese war fan. Once held by military leaders (such as daimyō) and priests in the past, it is used in the modern day by umpires in sumo wrestling.[1] Description Gunbai, from the Sino-Japanese roots meaning military-apportioned [fan], were a specialized form of fan used by samurai officers in Japan to communicate commands to their troops. Unlike regular fans, gu...

Caster SemenyaCaster Semenya pada 2018Informasi pribadiKewarganegaraanAfrika SelatanLahir7 Januari 1991 (umur 33)Pietersburg, Afrika SelatanAlma materNorth-West UniversityTinggi178 m (584 ft 0 in)Berat70 kg (154 pon) Karier sepak bolaKarier senior*Tahun Tim Tampil (Gol)2019– JVW F.C. * Penampilan dan gol di klub senior hanya dihitung dari liga domestikOlahragaOlahragaLariLomba800 meter, 1500 meterPrestasi dan gelarPeringkat pribadi terbaik400m: 49.62 NR600m: 1:...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 4th Secretariat of the Workers' Party of Korea – news · newspapers · books · scholar · JSTOR (February 2021) The 4th Secretariat of the Workers' Party of Korea (WPK)(4차 조선로동당 비서국), officially the Secretariat of the 4th Congress of th...
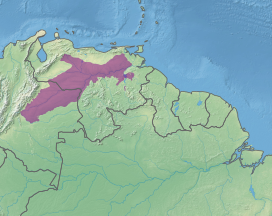
Tropical grassland ecoregion in Colombia and Venezuela This article is about the grassland and savanna region in South America. For other uses, see Llanos (disambiguation). LlanosThe Llanos in ColombiaLocation of the LlanosEcologyRealmNeotropicalBiometropical and subtropical grasslands, savannas, and shrublandsBorders List Apure–Villavicencio dry forestsGuianan lowland moist forestsGuianan piedmont and lowland moist forestsLa Costa xeric shrublandsOrinoco wetlandsNegro-Branco moist forests ...

كرنفال سوابيا، ألمانيا. كرنفال أو عيد المَرفَع[1] أو أيام الرفاع[2] أو الكزيرة[2] (الإنجليزية: Carnival) هو احتفال وإستعراض شعبي، يجمع بين السيرك والاحتفالات الشعبيّة التي تجوب الشوارع، وعادًة ما تكون هذه الاستعراضات في موسم الكرنفال. وتعتبر الكرنفالات تقليد كاثوليك...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) منتخب ليبيا لكرة القدم الخماسية بلد الرياضة ليبيا الطاقم واللاعبون المدرب ماتو ستكوفيتش مشاركات تعد�...

Funk carioca Données clés Origines stylistiques Miami bass, freestyle Origines culturelles Milieu des années 1980 ; Rio de Janeiro, Brésil Instruments typiques Boîte à rythmes, synthétiseur, échantillonneur, voix Genres dérivés Proibidão, funk melody, funk ostentação, funk ousadia, brega funk, electrofunk modifier Le funk carioca, aussi appelé funk brasileiro ou funky, — funk de favela ou baile funk dans le monde anglophone — est un genre de musique électron...

В Википедии есть статьи о других людях с такой фамилией, см. Коляденко. Александр Иванович Коляденко Дата рождения 1890 Дата смерти 24 апреля 1918(1918-04-24) Место смерти Алушта Гражданство Российская империя Род деятельности революционер Партия РСДРП(б)КПСС Александ�...

Maria Laach redirects here. For the Austrian town, see Maria Laach am Jauerling. Benedictine abbey situated in Glees, Germany This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2024) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in German. (May 2024) Click [show] for impo...

Città metropolitana di Palermocittà metropolitana Città metropolitana di Palermo – VedutaPalazzo Comitini, sede istituzionale LocalizzazioneStato Italia Regione Sicilia AmministrazioneCapoluogo Palermo Sindaco metropolitanoRoberto Lagalla (UdC) dal 20-6-2022 Data di istituzione4 agosto 2015 TerritorioCoordinatedel capoluogo38°06′56″N 13°21′41″E38°06′56″N, 13°21′41″E (Città metropolitana di Palermo) Superficie5 009,28 km² Abitanti1 1...



