Matriz semejante
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Naoto adalah nama Jepang. Tokoh-tokoh dengan nama Jepang ini antara lain: Pemain sepak bola Jepang Naoto Ando Naoto Arai Naoto Hiraishi Naoto Hori Naoto Ishikawa Naoto Kamifukumoto Naoto Kidoku Naoto Kono Naoto Matsuo Naoto Miki Naoto Misawa Naoto Mur...

Statistik orang dengan gangguan kecemasan menyeluruh di Amerika Serikat Gangguan kecemasan menyeluruh atau Generalized anxiety disorder (GAD) adalah gangguan kecemasan yang terjadi pada seseorang ditandai dengan rasa cemas berlebihan, khawatir dan tegang yang tidak terkendali. Kecemasan tersebut cenderung terjadi secara berulang dan tidak terkendali. Orang yang mengalami gangguan kecemasan menyeluruh biasanya dapat merasa cemas walaupun tidak sedang menghadapi situasi yang menegangkan.[1&...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Launch Pad card game – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this template message) Launch PadBox coverDesignersMelanie JamesIllustratorsAndy KurzenPublishersStratus GamesPublicationNovember 2010Years active2010 to presentGenresFamily, CardPlayers2 t...

Indian musician Aadesh ShrivastavaShrivastav with Vijeyta Pandit at the special screening of Bol Bachchan 21Born(1964-09-04)4 September 1964Jabalpur, Madhya Pradesh, IndiaDied5 September 2015(2015-09-05) (aged 51)Mumbai, Maharashtra, IndiaNationalityIndianOccupationsComposersingermusic arrangermusic producerYears active1990–2015SpouseVijayta Pandit Aadesh Shrivastava (4 September 1964 – 5 September 2015) was a music composer and singer of Indian music. Initially, he had worked a...

German general (1884–1963) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Georg Lindemann – news · newspapers · books · scholar · JSTOR (November 2012) (Learn how and when to remove this template message) You can help expand this article with text translated from the corresponding article in German. ...

Contea di DawsonconteaContea di Dawson – VedutaIl tribunale della contea di Dawson. LocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoLamesa Data di istituzione1876 TerritorioCoordinatedel capoluogo32°44′24″N 101°57′00″W / 32.74°N 101.95°W32.74; -101.95 (Contea di Dawson)Coordinate: 32°44′24″N 101°57′00″W / 32.74°N 101.95°W32.74; -101.95 (Contea di Dawson) Superficie2 336 km² Abitanti13&#...

Village in Estonia Village in Rapla County, EstoniaSadalaVillageSadalaLocation in EstoniaCoordinates: 59°07′00″N 24°53′51″E / 59.11667°N 24.89750°E / 59.11667; 24.89750Country EstoniaCounty Rapla CountyMunicipalityRapla ParishOfficial village2010Area • Total3.85 km2 (1.49 sq mi)Population (01.02.2010[1]) • Total10 • Density2.6/km2 (6.7/sq mi) Sadala is a village in Rapla Parish, Rapla...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Indoor stadium at the Dallas Cowboys headquarters Ford Center at The StarTostitos Championship Plaza, at the entrance to Ford Center at the Star. The plaza's field is a miniature 3⁄5 representation of an official field.Address9 Cowboys WayLocationFrisco, TexasCoordinates33°06′38″N 96°49′41″W / 33.1105°N 96.8281°W / 33.1105; -96.8281OperatorDallas CowboysCapacity12,000SurfaceHellas Matrix Helix TurfConstructionBroke groundAugust 22, 2014Opened2016Const...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

كاريزوسا (بالإسبانية: Carrizosa)[1] - بلدية - كاريزوسا (سيوداد ريال) كاريزوسا (سيوداد ريال) خريطة الموقع تقسيم إداري البلد إسبانيا [2] المقاطعة مقاطعة ثيوداد ريال خصائص جغرافية إحداثيات 38°50′30″N 2°59′34″W / 38.841666666667°N 2.9927777777778°W / 38.8...

Cet article concerne les épisodes diffusés de 2005 à 2022. Pour ceux diffusés entre 1963 et 1989, voir Liste des épisodes de Doctor Who (1963–1989). Pour ceux diffusés depuis 2023, voir Liste des épisodes de Doctor Who (depuis 2023). Cet article présente la liste des épisodes de la série télévisée britannique Doctor Who de 2005 à 2022. Doctor Who est une série de science-fiction produite et diffusée par la BBC depuis 1963. La première série, diffusée jusqu'en 1989, e...

2002 anthology by Stephen Baxter Evolution First edition coverAuthorStephen BaxterCountryUnited KingdomLanguageEnglishGenreScience fiction novelPublisherOrion Publishing GroupPublication date2002Media typePrint (hardback & paperback)Pages592 (DelRey Hardcover ed.)ISBN0-575-07342-X (first edition, paperback) & ISBN 0-575-07341-1 (hardback edition)OCLC50527130 Evolution is a collection of short stories that work together to form an episodic science fiction novel by author Step...

American philanthropic organization John Templeton FoundationFormation1987; 37 years ago (1987)FounderJohn TempletonHeadquartersWest Conshohocken, PennsylvaniaFieldsScientific researchReligious studiesOfficial language EnglishPresidentHeather Templeton DillRevenue (2016) $30.2 million[1]Expenses (2016)$182.2 million[1]Endowment$3.9 billion[2]Websitetempleton.org The John Templeton Foundation (Templeton Foundation) is a philanthropic organization that ...

Steyr AUG Steyr AUG A1 Jenis Senapan serbu Negara asal Austria Sejarah pemakaian Masa penggunaan 1978–sekarang Digunakan oleh Austria, Australia, Timor Timur,Irlandia, Indonesia, Luxembourg,Malaysia, Oman, Pakistan, Filipina,Selandia Baru, Arab Saudi, Tunisia,Amerika Serikat, Inggris Pada perang Timor Timur, Afganistan, Irak Sejarah produksi Tahun 1977 Produsen Steyr Mannlicher Diproduksi 1978— Varian Lihat Varian Spesifikasi Berat 3,6 kg (kosong) Panjang 790 mm...
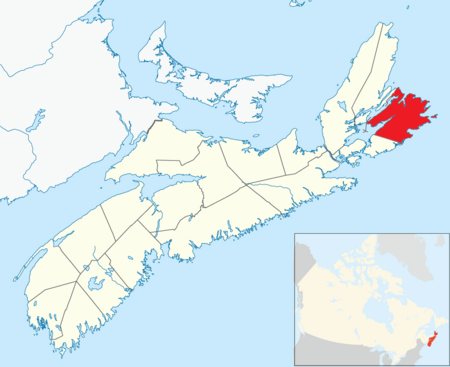
Place in Nova Scotia, CanadaDominionDominion Beach in Dominion, Nova ScotiaDominionLocation of Dominion, Nova ScotiaCoordinates: 46°12′37″N 60°01′30″W / 46.21028°N 60.02500°W / 46.21028; -60.02500CountryCanadaProvinces of CanadaNova ScotiaRegional MunicipalityCape Breton Regional MunicipalityIncorporated Town1906AmalgamatedAugust 1, 1995Population (2011) • Total1,953 • Change (2006-11)8.5%Time zoneUTC-4 (AST) • ...

British politician (born 1982) Layla MoranMPOfficial portrait, 2019Member of Parliamentfor Oxford West and AbingdonIncumbentAssumed office 8 June 2017[1]Preceded byNicola BlackwoodMajority14,894 (32.4%)Liberal Democrat portfolios2023-presentScience, Innovation and Technology2020-presentForeign, Commonwealth and Development Affairs2019–2020Digital, Culture, Media and Sport2017-2020Education Personal detailsBornLayla Michelle Moran (1982-09-12) 12 September 1982 (age 41)Hamme...

For the Soviet counterpart, see Northern Military District (Soviet Union). Northern Fleet Joint Strategic CommandОбъединённое стратегическое командование «Северный флот»Great emblem of the Northern FleetFounded1 December 2014Disbanded1 March 2024[1]Country RussiaTypeMilitary districtPart of Russian Armed ForcesGarrison/HQSeveromorskWebsiteOfficial websiteCommandersFinal CommanderAdmiral Alexander MoiseyevMilitary unit Russi...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Go NorthFilm posterSutradaraMatt OgensProduserJosh Gold Jay ThamesDitulis olehKyle Lierman Matt OgensPemeranJacob Lofland Sophie Kennedy Clark Patrick Schwarzenegger James BloorPenata musikGreg KuehnSinematograferJohn TiptonPenyuntingHal Honigsb...

Noncommutative extension of the complex numbers This article is about quaternions in mathematics. For other uses, see Quaternion (disambiguation). Quaternion multiplication table ↓ × → 1 i j k 1 1 i j k i i −1 k −j j j −k −1 i k k j −i −1 Left column shows the left factor, top row shows the right factor. Also, a b = b a {\displaystyle a\mathbf {b} =\mathbf {b} a} and − b = ( − 1 ) b {\displaystyle -\mathbf {b} =(-1)\mathbf {b} } for a &#x...

























