Kernel (teoría de categorías)
|
Read other articles:
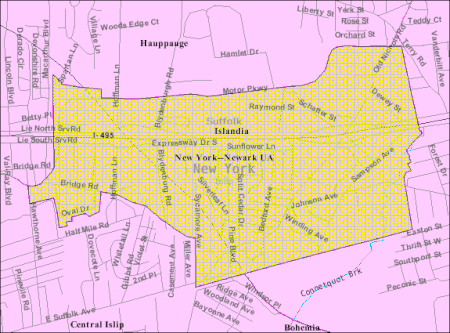
أيلانديا الإحداثيات 40°48′17″N 73°10′22″W / 40.8047°N 73.1728°W / 40.8047; -73.1728 [1] تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة سوفولك خصائص جغرافية المساحة 5.748133 كيلومتر مربع5.749337 كيلومتر مربع (1 أبريل 2010) ارتفاع 20 متر ...

العلاقات البوتانية الفانواتية بوتان فانواتو بوتان فانواتو تعديل مصدري - تعديل العلاقات البوتانية الفانواتية هي العلاقات الثنائية التي تجمع بين بوتان وفانواتو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقار...

1961 Polish parliamentary election ← 1957 16 April 1961 1965 → All 460 seats in the Sejm First party Leader Władysław Gomułka Party FJN - PZPR Seats won 460 Seat change 1 Premier before election Józef Cyrankiewicz PZPR New Premier Józef Cyrankiewicz PZPR Parliamentary elections were held in Poland on 16 April 1961.[1] They were the third elections to the Sejm, the parliament of the People's Republic of Poland, and fourth in Communist...

United StatesFIBA ranking1stFIBA zoneFIBA AmericasNational federationUSA BasketballCoachSue PhillipsWorld ChampionshipsAppearances6Medals Gold: 2010, 2012, 2014, 2018, 2022 Bronze: 2016Americas ChampionshipsAppearances5Medals Gold: 2009, 2011, 2013, 2017 Bronze: 2015 The USA women's national under-17 basketball team is the women's basketball team, administered by USA Basketball, that represents the United States in international under-17 and under-16 (under age 17 and under age 16) women's ba...

Town in East Sussex, England Human settlement in EnglandBattleView along the High Street towards the abbeyBattleLocation within East SussexArea31.8 km2 (12.3 sq mi) [1]Population6,800 (2021)[2]• Density503/sq mi (194/km2)OS grid referenceTQ747160• London48 miles (77 km) NNWDistrictRotherShire countyEast SussexRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townBATTLEPostcode districtTN33D...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

City in Georgia, United StatesBuena Vista, GeorgiaCityBuena Vista in 2012Location in Marion County and the state of GeorgiaCoordinates: 32°19′6″N 84°30′58″W / 32.31833°N 84.51611°W / 32.31833; -84.51611CountryUnited StatesStateGeorgiaCountyMarionArea[1] • Total3.27 sq mi (8.48 km2) • Land3.22 sq mi (8.34 km2) • Water0.06 sq mi (0.14 km2)Elevation719 ft (219 m...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

نيوم الاسم الكامل نادي نيوم الرياضي السعودي تأسس عام 1965 [1] الملعب مدينة الملك خالد الرياضية تبوك، السعودية(السعة: 12,000) البلد السعودية الدوري دوري الدرجة الثانية السعودي 2022/23 2022/23 الإدارة المالك نيوم الرئيس معاذ العوهلي المدرب عفوان الغربي الطقم الأساسي الطقم الاحت...

Polemone IIEffigie di Polemone su una moneta; al rovescio, effigie di NeroneSovrano di Ponto, Colchide e CiliciaIn carica38 –62 (Ponto e Colchide) 74 (Cilicia) PredecessorePitodorida del Ponto Nome completoMarco Antonio Polemone Pitodoro Nascita12 a.C./11 a.C. Morte74 PadrePolemone Pitodoro MadrePitodorida del Ponto ConsorteGiulia Berenice FigliBereniciano e Ircano ReligionePaganesimo, poi giudaismo, poi paganesimo Marco Antonio Polemone Pitodoro (in greco: Μάρκος Ἀντώ...

31st season of top-tier football league in Argentina Football league seasonPrimera DivisiónSeason1922Dates9 April 1922 – 14 January 1923ChampionsHuracán (AFA) Independiente (AAmF)← 1921 1923 → The 1922 Argentine Primera División was the 31st season of top-flight football in Argentina. Huracán won its second consecutive championship, while Independiente obtained its first title, the Asociación Amateurs de Football championship. Final tables Asociación Argentina de Football - Copa C...

American medical training program Advanced trauma life supportGeneral informationNamesAdvanced trauma life supportAbbreviationATLSFieldMedicineHistoryInventorJames K. Styner, Paul 'Skip' CollicottInvention date1978DescriptionOrganizerAmerican College of SurgeonsParticipantsemergency physicians, paramedics and other advanced practitionersDuration3 days (for hybrid course)[1]Frequency1 week – 1 monthAdditionallyRelated coursesAdvanced cardiac life supportPediatric advanced life suppor...

Association football club based in Bloenfontein, South Africa Football clubRoses UnitedFull nameRoses United Football ClubFounded2009GroundWestdene Stadium, BloemfonteinCapacity5,000ChairmanMax TshabalalaCoach Benjamin ReedLeagueNational First Division2011–12Vodacom League winners Home colours Away colours Roses United is a South African football club based in Bloemfontein, Free State province that plays in the National First Division. The club was founded in 2009, where they acquired the C...

American steamship For other ships with the same name, see USS Massachusetts. This illustration of USS Massachusetts appeared in Cassier's Magazine, December 1894. History United States Launched1845 Acquired1 August 1849 Commissioned1 August 1849 DecommissionedMay 1859 In service17 June 1863 Out of serviceFebruary 1867 Fatesold, 15 May 1867 General characteristics Tonnage765 Length178 ft (54 m) Beam32 ft 2 in (9.80 m) Draft15 ft (4.6 m) Propulsion steam engi...

Stasiun Vespucio NorteStasiun angkutan cepat di SantiagoStasiun Vespucio NorteLokasiAmérico Vespucio dan Av. Principal Ignacio Carrera PintoKoordinat33°22′52.18″S 70°38′40.30″W / 33.3811611°S 70.6445278°W / -33.3811611; -70.6445278Koordinat: 33°22′52.18″S 70°38′40.30″W / 33.3811611°S 70.6445278°W / -33.3811611; -70.6445278PemilikMetro S.A.Jalur Jalur 2Jumlah peronRusukJumlah jalur2LayananBus TransantiagoKonstruksiTinggi ...

Боксна XXVI Олімпійських іграх Місце проведення Alexander Memorial Coliseum, АтлантаДати20 липня 1996 — 4 серпня 1996Учасників355 з 97 країн← 19922000 → Змагання з боксу на літніх Олімпійських іграх 1996 проходили з 20 липня по 4 серпня. Було розіграно 12 комплектів нагород. Бокс на л�...

Untuk Sekutu Perang Dunia I, lihat Blok Sekutu dalam Perang Dunia I. Generalissimo Chiang Kai-shek (Republik Tiongkok) Franklin D. Roosevelt (Amerika Serikat) dan Winston Churchill (Britania Raya) bertemu di Konferensi Kairo tahun 1943 semasa Perang Dunia II. Blok Sekutu pada Perang Dunia II adalah negara-negara yang berperang bersama melawan Blok Poros (Jerman Nazi, Kerajaan Italia, dan Kekaisaran Jepang, dan lain-lain) dari 1939 sampai 1945. Anggota Lima Besar dan Lima Polisi adalah lima Bl...

City in Nangarhar Province, Afghanistan For other uses, see Jalalabad (disambiguation). Not to be confused with Jalal-Abad. City in Nangarhar Province, AfghanistanJalalabad جلالآبادCityFrom top counter-clockwise: An aerial view of a section of Jalalabad, Irrigation fields in Jalalabad, Jalalabad Cricket Stadium, Jalalabad in January 2011, Jalalabad Bridge, Governor's House in JalalabadJalalabadLocation in AfghanistanShow map of AfghanistanJalalabadJalalabad (Hindu-Kush)Show map of ...

Bus route in Zhengzhou, China B2OverviewSystemZhengzhou BRTOperatorZhengzhou Bus Communication CorporationVehicleYutong ZK6180CHEVNPG3 (18m)Yutong ZK6125CHEVNPG4 (12m)Yutong E12 (12m)LiveryGreen (18m articulated bus and E12)Brown (other 12m buses)StatusOperationalBegan service26 January 2014[1]RouteLocaleZhengzhouStartDaxie B/TEndZhongzhou AvenueLength23 km (14 mi)Stops32ServiceLevelDailyOperates6:00 am – 9:30 pm Route map Legend Daxie Bus Terminus Qianxiangwanhechen...

