Hipercubo
|
Read other articles:

Direktorat Jenderal Planologi Kehutanan dan Tata Lingkungan Kementerian Lingkungan Hidup dan Kehutanan Republik IndonesiaGambaran umumDasar hukumPeraturan Presiden Nomor 16 Tahun 2015Susunan organisasiDirektur Jenderal-Situs webpktl.menlhk.go.id Direktorat Jenderal Planologi Kehutanan dan Tata Lingkungan merupakan unsur pelaksana pada Kementerian Lingkungan Hidup dan Kehutanan Republik Indonesia yang berada di bawah dan bertanggung jawab kepada Menteri Lingkungan Hidup dan Kehutanan Repu...

Assemblée consultative provisoire d'Alger Conseil national (Régime de Vichy)XVIe législature de la IIIe République française (République française)XXIe mandat sénatorial de la IIIe République française (République française) Assemblée consultative provisoire de Paris Présidence Présidence Félix Gouin Élection Ordonnance du Comité français de libération nationale Données clésDonnées clés modifier Assemblée consultative provisoire de Paris Assemblé...

Untuk sprinter Amerika Serikat, lihat Emerson Spencer. Bud SpencerSpencer pada 2015LahirCarlo Pedersoli(1929-10-31)31 Oktober 1929Napoli, Kerajaan ItaliaMeninggal27 Juni 2016(2016-06-27) (umur 86)Roma, ItaliaMakamCampo Verano, Roma, ItaliaAlmamaterUniversitas Sapienza RomaPekerjaanPemeranPerenang profesionalPemain polo airTahun aktif1950–2010Suami/istriMaria Amato (m. 1960)Anak3PenghargaanDavid di Donatello Special AwardSitus webbudspencerofficial.co...

Coppa Titano 2012-2013Coppa di San Marino Competizione Coppa Titano Sport Calcio Edizione 55ª Organizzatore FSGC Date dal 1º settembre 2012al 29 aprile 2013 Luogo San Marino Partecipanti 15 Risultati Vincitore La Fiorita(3º titolo) Secondo San Giovanni Statistiche Incontri disputati 67 Gol segnati 185 (2,76 per incontro) Cronologia della competizione 2011-2012 2013-2014 Manuale La Coppa Titano 2012-2013 è iniziata il 1º settembre 2012 ed è terminata il 29...

1984 United States Supreme Court caseChevron U.S.A. v. Natural Res. Def. CouncilSupreme Court of the United StatesArgued February 29, 1984Decided June 25, 1984Full case nameChevron U.S.A., Inc. v. Natural Resources Defense Council, Inc., et al.Docket nos.82-100582-124782-1591Citations467 U.S. 837 (more)104 S. Ct. 2778; 81 L. Ed. 2d 694; 21 ERC (BNA) 1049; 14 Envtl. L. Rep. 20,507; 52 U.S.L.W. 4845; 1984 U.S. LEXIS 118ArgumentOral argumentCase historyPriorNatural Resources Defense Council v. ...

Association football club in England Football clubAbbey RangersFull nameAbbey Rangers Football ClubNickname(s)The AbbeyFounded1976GroundAddlestone Moor, AddlestoneChairmanNick RileyManagerMike Woolgar & Paul JohnsonLeagueCombined Counties League Premier Division South2022–23Combined Counties League Premier Division South, 4th of 20 Home colours Away colours Abbey Rangers Football Club is a football club based in Addlestone, England. The club are currently members of the Combined Countie...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Pour un article plus général, voir Cannabis. Extrait liquide de cannabis, distribué par une pharmacie américaine au début du XXe siècle. Vaporisateur avec tube flexible. Le cannabis médical (appelé aussi cannabis thérapeutique, marijuana médicale ou marijuana thérapeutique[1]) désigne le Cannabis sativa (désignation botanique du chanvre) en tant que plante médicinale, et, par extension, l'ensemble des dizaines de phyto-cannabinoïdes destinés à un usage purement médical...

Part of Coly-Saint-Amand in Nouvelle-Aquitaine, FranceSaint-Amand-de-ColyPart of Coly-Saint-Amand Coat of armsLocation of Saint-Amand-de-Coly Saint-Amand-de-ColyShow map of FranceSaint-Amand-de-ColyShow map of Nouvelle-AquitaineCoordinates: 45°03′52″N 1°14′53″E / 45.0644°N 1.2481°E / 45.0644; 1.2481CountryFranceRegionNouvelle-AquitaineDepartmentDordogneArrondissementSarlat-la-CanédaCantonVallée de l'HommeCommuneColy-Saint-Amand Area126.40 km2 (10.19&...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Jon Dahl Tomasson Informasi pribadiNama lengkap Jon Dahl TomassonTanggal lahir 29 Agustus 1976 (umur 47)Tempat lahir Roskilde, DenmarkTinggi 1,82 m (5 ft 11+1⁄2 in)Posisi bermain PenyerangInformasi klubKlub saat ini FeyenoordNomor 11Karier junior1981–19851985–1992 Solrød BKKøge BKKarier senior*Tahun Tim Tampil (Gol) 1992–19941994–19971997–19981998–20022002–20052005–20072007–20082008– Køge BKSC HeerenveenNewcastle UnitedFeyenoordMilanStuttgartV...

This article has no lead section. Please improve this article by adding one in your own words. (December 2022) (Learn how and when to remove this message) Below is a list of ships being built by the United States Navy. Commissioned ships Under construction Class Ship Pennant no. Builder Type Laid down Launched Commissioning Status Source Aircraft Carrier Gerald R. Ford John F. Kennedy CVN-79 Newport News Shipbuilding Aircraft carrier 22 August 2015 29 October 2019 2024 (planned) Fitting out ...

Karl Heinrich Ulrichs (1825–1895), a pioneer of LGBT+ rights This is a list of important events relating to the LGBT community from 1801 to 1900. The earliest published studies of lesbian activity were written in the early 19th century. 1800s 1802 The French Republic annexes Piedmont, thus extending the French Penal Code of 1791 to the annexed territory. 1803 The last recorded state sanctioned execution for male same-sex sodomy occurs in the Batavian Commonwealth and continental Europe. ...

Questa voce o sezione sugli argomenti nobili tedeschi e militari tedeschi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Massimiliano Guglielmo di Hannover e Brunswick-Lüneburg NascitaBad Iburg, 13 dicembre 1666 MorteVienna, 16 luglio 1726 (59 anni) PadreErnesto Augusto, Elettore di Hannover MadreSofia del Palatinato Massimiliano Guglielmo di...

إمام أهل الشَّام والمغرب والأندلُس عبدُ الرحمٰن الأوزاعي أبو عمرو عبد الرحمٰن بن عمرو بن يُحمِد الأوزاعي تخطيط اسم الإمام الأوزاعي مُلحق بِلقبه معلومات شخصية الميلاد 88 هـ/707مبعلبك، الشَّام، الدولة الأموية الوفاة 157هـ/774مبيروت، الشَّام، الدولة العباسية سبب الوفاة �...

Gran Premio di Brno 2005 Prova del mondiale SuperbikeProva 7 su 12 del 2005 Data 17 luglio 2005 Luogo Circuito di Brno Percorso 5,403 km Risultati Superbike gara 1 423ª gara nella storia del campionato Distanza 20 giri, totale 108,06 km Pole position Giro più veloce Troy Corser Troy Corser Suzuki in 2:02.694 Suzuki in 2:03.812 (nel giro 4 di 20) Podio 1. Troy CorserSuzuki 2. James ToselandDucati 3. Régis LaconiDucati Superbike gara 2 424ª gara nella storia del campionato Distan...

Meistriliiga2016 Généralités Sport Football Organisateur(s) EJL Édition 26e Date Du 4 mars au 19 novembre 2016 Participants 10 équipes Site web officiel Site officiel Palmarès Tenant du titre FC Flora Tallinn Promu(s) en début de saison JK Tarvas Rakvere Vainqueur FC Infonet Tallinn Meilleur(s) buteur(s) Evgeny Kabaev (25) Navigation Meistriliiga 2015 Meistriliiga 2017 modifier La saison 2016 du Championnat d'Estonie de football est la 26e de l'élite du football estonien. Les dix mei...

Pakistani mobile payment service provider This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (April 2024) (Learn how and when to remove this message) JazzCashFormerlyMobiCashCompany typePrivateIndustryMobile financial servicesFoundedNovember 29, 2012; 11 years ago (2012-11-29)[1]Key peopleA...

У этого термина существуют и другие значения, см. Сосенки. ДеревняСосенки 55°33′49″ с. ш. 37°26′23″ в. д.HGЯO Страна Россия Субъект Федерации Москва Административный округ Новомосковский Поселение Сосенское История и география Прежние названия Соснино Высота це...
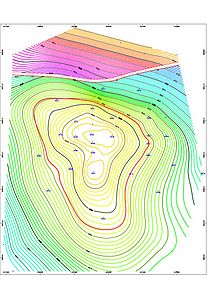
Logiciel de cartographie géologique affichant une carte de structure générée pour un réservoir de gaz et de pétrole de 2 590 m de profondeur dans le champ terrestre, paroisse de Vermilion, Erath, Louisiane. L'espace de gauche à droite, près du haut de la carte de contour, indique une ligne de faille. Cette ligne de faille se situe entre les courbes de niveau bleu/vert et les courbes de niveau violet/rouge/jaune. La fine ligne de contour circulaire rouge au milieu de la cart...

























































































