Grafo de Heawood
| |||||||||||||||||||||||||||||||||||||
Read other articles:

Kalpana SarojKalpana SarojLahir1961 (1961) (usia 63)Roperkheda, Maharashtra, IndiaTempat tinggalMumbai, IndiaKebangsaanIndianPekerjaanChief Executive Officer, Kamani TubesKekayaan bersih US$ 112 millionSuami/istriSamir Saroj (m. 1980; meninggal 1989)ShubhkaranAnakSeema Saroj, Amar SarojSitus webwww.kalpanasaroj.com Kalpana Saroj adalah wirausaha perempuan India dan pembicara TEDx,[1] lahir di desa Roperkheda di Maharashtra...

Ekonomi EtiopiaBank Komersial Etiopia di Addis AbabaMata uangBirr (ETB) (ብር)Tahun fiskal8 – 7 Juli (1 ሐምሌ – 30 ሰኔ)Organisasi perdaganganUni Afrika, Organisasi Perdagangan Dunia (pengamat)StatistikPDB$194,980 miliar (KKB)$78,434 miliar (nominal)(IMF, Perk. 2017[update])[1]Pertumbuhan PDB 10,2% (2014) 6,5% (perkiraan 2016)[2]PDB per kapita$2.104 (KKB)$846 (nominal)(IMF, Perk. 2017[update])[1]PDB per sektorAgrikultur (36,7%), jasa (47,1%)...

1914 film by Allan Dwan Wildflower1914 lobby posterDirected byAllan DwanWritten byAllan Dwan (scenario)Eve Unsell (scenario)Story byMary GermaineProduced byAdolph ZukorDaniel FrohmanStarringMarguerite ClarkHarold LockwoodJack PickfordCinematographyHenry Lyman BroeningProductioncompanyFamous Players–Lasky CorporationDistributed byParamount PicturesRelease date October 15, 1914 (1914-10-15) Running time4 reels; 4,163 feetCountryUnited StatesLanguagesSilentEnglish intertitles Wi...

Erling Haaland Haaland bermain untuk Manchester City pada 2023Informasi pribadiNama lengkap Erling Braut Haaland[1]Tanggal lahir 21 Juli 2000 (umur 23)[2]Tempat lahir Leeds, Yorkshire Barat, InggrisTinggi 194 cm (6 ft 4 in)[3]Posisi bermain PenyerangInformasi klubKlub saat ini Manchester CityNomor 9Karier junior2005–2016 BryneKarier senior*Tahun Tim Tampil (Gol)2015–2016 Bryne 2 14 (18)2016–2017 Bryne 16 (0)2017 Molde 2 4 (2)2017–2019 Molde...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Vous lisez un « article de qualité » labellisé en 2009. Il fait partie d'un « bon thème ». Métro ligne 10 La station Cluny - La Sorbonne. Réseau Métro de Paris Terminus Boulogne - Pont de Saint-CloudGare d'Austerlitz Communes desservies 2 Histoire Mise en service 30 décembre 1923 Dernière extension 2 octobre 1981 Exploitant RATP Infrastructure Conduite (système) Conducteur Exploitation Matériel utilisé MF 67 (30 rames au 8 août 2018) Points d’arrê...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Combined military forces of the United States US Forces redirects here. For the Midnight Oil song, see US Forces (song). This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (June 2023) (Learn how and when to remove this message) United States Armed Forces Emblems of the U.S. Armed Forces' service branchesFounded14 June 1775; 248 years ago (1775-06-14)[a]Service branches U.S. Army U.S. Marine...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

Sportswear and leisure wear company Oysho España, S.A.OYSHO Store in London (United Kingdom)Company typeSociedad AnónimaIndustryRetailFounded2001HeadquartersTordera,[1] Barcelona, SpainNumber of locations457 (2023)[2]Area servedWorldwideProductsClothingParentInditexWebsitewww.oysho.com Oysho is a fashion chain specialising in sport and leisure, founded in 2001. Its headquarters are in Tordera (Barcelona). Oysho is part of the Inditex group and operates in more than 50 countr...

Secondary school in Altens, Aberdeen, ScotlandLochside AcademyThe exterior of the school in March 2020.AddressWellington CircleAltens, Aberdeen, AB12 3JGScotlandCoordinates57°06′41″N 2°05′58″W / 57.1113°N 2.0994°W / 57.1113; -2.0994InformationTypeSecondary schoolEstablishedAugust 23, 2018 (2018-08-23)Local authorityAberdeen City CouncilHead teacherJustin NoonStaff103GenderCo-educationalAge11 to 18Number of pupils1,580Capacity1,350Colour(...

Società storica lombardaIl primo volume del Giornale dell'Archivio Storico Lombardo (1874) AbbreviazioneSSL TipoSocietà storica Fondazione1873 Sede centrale Milano Area di azioneLombardia Sito web e Sito web Modifica dati su Wikidata · Manuale La Società Storica Lombarda è un'associazione di studi storici, umanistici e scientifici costituita a Milano nel 1873 dallo storico milanese Cesare Cantù. È formata da 450 soci e insieme ad altre 30 associazioni di tutte le regioni d'Italia ...

Russian and Soviet physicist and mathematician (1888–1925) This article is about the Russian cosmologist. For the Russian astrophysicist, see Alexei Fridman. For the Polish Orthodox Jewish rabbi, see Alexander Zusia Friedman. In this name that follows Eastern Slavic naming customs, the patronymic is Alexandrovich and the family name is Friedmann. Alexander FriedmannАлександр ФридманBornAlexander Alexandrovich Friedmann(1888-06-16)June 16, 1888Saint Petersburg, Russian Em...

1991 Valencian regional election ← 1987 26 May 1991 1995 → All 89 seats in the Corts Valencianes45 seats needed for a majorityOpinion pollsRegistered2,916,465 6.9%Turnout2,019,411 (69.2%)5.3 pp First party Second party Third party Leader Joan Lerma Pedro Agramunt Héctor Villalba Party PSOE PP UV Leader since 31 July 1979 15 December 1990 1991 Leader's seat Valencia Valencia Valencia Last election 42 seats, 41.3% 25 seats, 24.7%[a&#...

公使可以指: 特命全權公使(Envoy Extraordinary and Minister Plenipotentiary,簡稱Envoy),為公使館的館長,以及外交官體系中僅次於大使、級別第二高的外交官銜。 公使(瑞典语:Minister (diplomat))(Minister),附派於大使館內的外交官,可作為副館長擔任大使館的二把手。 常駐公使(德语:Ministerresident)(Minister Resident,亦稱駐辦公使),為1818年亞琛會議後始設的外交官銜,1961�...

Casale sul Sile— Comune —Comune di Casale sul Sile Vị trí của Casale sul Sile Casale sul SileXem bản đồ ÝCasale sul SileXem bản đồ VenetoVị trí của Casale sul Sile tại ÝQuốc giaÝVùngVenetoTỉnhTreviso (TV)Thủ phủCasale sul Sile FrazioniConscio, LughignanoDiện tích[1] • Tổng cộng26 km2 (10 mi2)Dân số (30 tháng 11 năm 2008)[3] • Tổng cộng12.418 ...
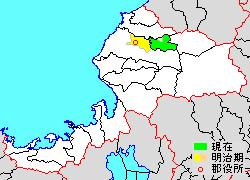
令制国一覧 > 北陸道 > 越前国 > 吉田郡 日本 > 中部地方 > 福井県 > 吉田郡 福井県吉田郡の位置(緑:永平寺町 黄:明治期 薄緑:後に他郡から編入した区域) 吉田郡(よしだぐん)は、福井県(越前国)の郡。 人口18,313人、面積94.43km²、人口密度194人/km²。(2024年9月1日、推計人口) 以下の1町を含む。 永平寺町(えいへいじち...

Pour les articles homonymes, voir Pontarlier (homonymie). Pontarlier De haut en bas, de gauche à droite : panorama de la ville depuis le Larmont ; la rue de la République et la mairie ; la rue de la République la nuit ; la place Saint-Bénigne ; la grande fontaine ; l'église Saint-Bénigne ; la façade du théâtre Bernard-Blier ; chemin de promenade sur les berges du Doubs ; la porte Saint-Pierre ; la rue de la République. Blason Logo A...






