Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

2004 single by Enrique Iglesias Not in LoveSingle by Enrique Iglesias featuring Kelisfrom the album 7 Released2 February 2004 (2004-02-02)Length3:42 (album version)3:41 (radio mix featuring Kelis)LabelInterscopeSongwriter(s)Enrique IglesiasPaul BarryMark TaylorFernando GaribaySheppard SolomonVictoria HornKelis Rogers[1]Producer(s)Enrique IglesiasMark TaylorEnrique Iglesias singles chronology Addicted (2003) Not in Love (2004) Do You Know? (The Ping Pong Song) (2007)...

Le département français des Landes est un département créé le 4 mars 1790 en application de la loi du 22 décembre 1789, à partir de l'ancienne province de Gascogne. Les 327 actuelles communes, dont presque toutes sont regroupées en intercommunalités, sont organisées en 15 cantons permettant d'élire les conseillers départementaux. La représentation dans les instances régionales est quant à elle assurée par 16 conseillers régionaux. Le département est également découpé en 3...

Halaman ini berisi artikel tentang salah satu bank pendahulu Bank Permata. Untuk bank pembangunan daerah Bali, lihat Bank BPD Bali. PT Bank Bali TbkJenisPublikIndustriPerbankan dan komponennyaNasibDileburkanPendahuluBank Dharma UsahaPenerusBank PermataDidirikan17 Desember 1954PendiriDjaja RamliDitutup18 Oktober 2002KantorpusatJakarta, IndonesiaTokohkunciRudy Ramli (Presiden Direktur)ProdukKeuangan PT Bank Bali Tbk adalah bank yang pernah ada di Indonesia hingga 2002. Bank ini didirikan pada t...

Untuk kegunaan lain, lihat Sekai no Owari (disambiguasi). Sekai no Owari世界の終わりInformasi latar belakangNama lainセカオワ (SekaOwa)AsalTokyo, JepangGenreJ-pop, indie pop, pop rock, alternative rockTahun aktif2007–sekarangLabelLastrum (2009–2010)Toy's Factory (2011–sekarang)Artis terkaitChrysanthemum Bridge, Earth CompanySitus websekainoowari.jpAnggotaFukase (vocals, guitar)Nakajin (leader, producer, guitar)Saori (piano, stage production)DJ Love (DJ, Sound Selection) Sekai ...

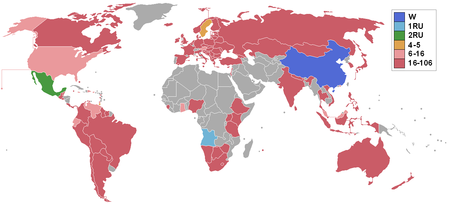
Beauty pageant edition This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Miss World 2007 – news · newspapers · books · scholar · JSTOR (December 2015) (Learn how and when to remove this message) Miss World 2007Miss World 2007 Zhang ZilinDate1 December 2007PresentersAngela ChowFernando AllendeEntertainmentDunca...

Pour les articles homonymes, voir Village (homonymie). Un village rural chinois typique à Hainan.En république populaire de Chine, un village (chinois : 村 ; pinyin : cūn), officiellement une division villageoise (村级行政区, cūn jí xíngzhèngqū) est une division administrative de bas niveau servant d'unité organisationnelle fondamentale pour la population rurale (par exemple pour le recensement et le système postal). Les divisions locales de base telles...

Political party in South Africa Dikwankwetla Party of South Africa LeaderMoeketsi LebesaFounderKenneth MopeliFounded1974HeadquartersQwaQwa, Free State, South AfricaPolitics of South AfricaPolitical partiesElections This article is part of a series on thePolitics ofSouth Africa Constitution Bill of Rights Executive President Cyril Ramaphosa Deputy President Paul Mashatile Cabinet Departments Shadow Cabinet Legislature National Council of Provinces Chairperson Amos Masondo National Assembly Spe...

Surface formed by rotating an ellipse For spheroids in cell culturing, see 3D cell culture. For rotating equilibrium spheroids, see Maclaurin spheroid and Jacobi ellipsoid. For the type of archaeological artifact, see Spheroid (lithic). Spheroids with vertical rotational axes oblate prolate A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equ...

Jackson Memorial Hospital in Miami, the primary teaching hospital of the University of Miami's Leonard M. Miller School of Medicine and the largest hospital in the United States with 1,547 beds[1] This article contains links to lists of hospitals in the United States, including U.S. States, the national capital of Washington, D.C., insular areas, and outlying islands. Links to more detailed state lists are shown.[2] U.S. states As of 2020, there were 5,250 acute care and crit...

Dinis redirects here. For other uses, see Dinis (disambiguation). King Denis redirects here. For the English composer, see Denis King. King of Portugal DenisKing Denis in the Castilian manuscript Compendium of Chronicles of Kings (...) (c. 1312–1325)King of PortugalReign16 February 1279 – 7 January 1325PredecessorAfonso IIISuccessorAfonso IVBorn9 October 1261Lisbon, PortugalDied7 January 1325 (aged 63)Santarém, PortugalBurialSt. Denis Convent, Odivelas, PortugalSpouse Elizabeth of Aragon...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (September 2018) (Learn how and when to remove this message) This article needs addi...

This article is about the river in Southern Ontario. For the river in England, see River Welland. Not to be confused with Chippewa River (Ontario). River in Southern Ontario Welland RiverChippawa CreekA boat on the riverLocationCountryCanadaProvinceOntarioCitiesWellandNiagara FallsPhysical characteristicsSource  • coordinates43°08′44″N 79°56′18″W / 43.14542°N 79.93847°W / 43.14542; -79.93847 • elevationapprox. 248&#...

For related races, see 2024 United States state legislative elections. Not to be confused with 2024 United States House of Representatives elections in Arizona. 2024 Arizona House of Representatives elections ← 2022 November 5, 2024 2026 → All 60 seats in the Arizona House of Representatives31 seats needed for a majority   Leader Ben Toma(retiring) Lupe Contreras Party Republican Democratic Leader since January 9, 2023 June 21, 2023 Leader's seat 27thR...

Untuk kegunaan lain, lihat Vista (disambiguasi). VistaLagu oleh FiestarSisi-BWickedSea of MoonlightDirilis31 Agustus 2012Format Maxi single Digital download Direkam2012GenreDance-popDurasi3:36LabelLOEN EntertainmentPenciptaKim In-ah, KZ Vista adalah singel debut dari grup vokal wanita asal Korea Selatan Fiestar. Singel ini dirilis pada tanggal 31 Agustus 2012 oleh LOEN Entertainment.[1] Daftar lagu No.JudulLirikMusikArrangementDurasi1.VistaKim In-ahKZKZ3:312.Wicked (featuring Tiger JK...

No. 113 Squadron RCAFActive1937–1939, 1942–1944Disbanded10 August 1944Country CanadaAllegiance CanadaBranch Royal Canadian Air ForceRoleBomber ReconnaissancePart ofRCAF Eastern Air CommandGarrison/HQRCAF Station Yarmouth, RCAF Station Chatham, RCAF Station TorbayEngagementsSecond World War Battle of the Atlantic Battle of the St. Lawrence Battle honoursNorth-West Atlantic 1942–1944[1]InsigniaSquadron CodesBT (Feb–May 1942), LM (Jun–Oc...

ポケットモンスター (アニメ) > ポケットモンスター (OVA) 「ポケットモンスター（OVA）」は、ゲームソフト『ポケットモンスターシリーズ』を原作とするテレビアニメ『ポケットモンスター』のオリジナル・ビデオ・アニメーション(OVA)作品について解説する。便宜上、全日空の機内上映で初公開されたアニメ作品などについても、ここで記述する。 ピカチュウの�...

ミラキュラス レディバグ&シャノワール Miraculous, les aventures de Ladybug et Chat Noir ジャンル 変身ヒロイン/ヒーロー アニメ：ミラキュラス レディバグ&シャノワールMiraculous: Tales of Ladybug & Cat Noir 原作 トーマス・アストリュック 監督 トーマス・アストリュッククリステル・アブグラル（シーズン2）ウィルフレッド・ペイン（シーズン2）ジュン・バイオレット（シー...

Topological invariant in mathematics This article is about Euler characteristic number. For Euler characteristic class, see Euler class. For Euler number in 3-manifold topology, see Seifert fiber space. In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2017) (Learn how and when to remove this message) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page...