Ecuación de Burgers
|
Read other articles:

Ezzard CharlesStatistikNama asliEzzard Mack CharlesNama panggilan Cincinnati Cobra Dinilai pada Middleweight Light-heavyweight Heavyweight Tinggi6 ft 0 inMencapai73 inLahir(1921-07-07)7 Juli 1921Lawrenceville, Georgia, U.S.Meninggal28 Mei 1975(1975-05-28) (umur 53)Chicago, Illinois, U.S.SikapOrthodoxCatatan tinjuTotal perkelahian121Menang95Menang oleh KO52Kalah25Imbang1 Rekam medali Men's amateur boxing Cincinnati Golden Gloves 1937 Cincinnati Welterweight 1938 Cincinnati Welterweight 19...

Legio X FretensisPeta Kekaisaran Romawi pada tahun 125 M pada masa Kaisar Hadrianus. Peta ini menunjukkan lokasi LEGIO X FRETENSIS yang sedang ditugaskan di Hierosolima (Yerusalem) dari tahun 73 M hingga abad ke-4Aktif41 SM hingga setelah tahun 410NegaraKekaisaran RomawiTipe unitLegiun RomawiMarkasYudea (20-an SM) Suriah (sekitar 6-66) Yerusalem (sekitar 73-akhir abad ke-3) Aila (akhir abad ke-3-setelah 410-an)JulukanFretensis, dari SelatMaskotTaurus, kapal, Neptunus, babi hutanPertempuranPer...

Icelandic newspaper Dagblaðið VísirTypeOnline newspaperFormatTabloid (formerly)Owner(s)Torg ehf.EditorBjörn ÞorfinnssonFounded1981; 43 years ago (1981)HeadquartersKalkofnsvegur 2, 101 Reykjavík108 ReykjavíkCountryIcelandISSN1021-8254Websitewww.dv.isMedia of IcelandList of newspapers DV (Dagblaðið Vísir) is an online newspaper in Iceland published by Torg ehf. It came into existence as a daily newspaper in 1981[1] when two formerly independent newspapers, V�...

Spanish military officer José María Barreiro ManjónJose Maria Barreiro, potrait c. 1818, National Museum of ColombiaBornAugust 20, 1793Cadiz, SpainDiedOctober 11, 1819Santa Fe, New GranadaCause of deathExecution by firing squadAllegianceSpainService/branchSpanish ArmyYears of service1808–1819RankColonelCommands heldIII Division Expeditionary Army of Costa FirmeBattles/warsPeninsular WarColombian War of Independence José María Barreiro Manjón (August 20, 1793 – October 11, ...

Mausoleum in Bardaskan County, Iranian national heritage site Tomb of Abdolabadآرامگاه عبدلآبادLocationJolgeh, Shahrabad, Abdolabad, Bardaskan, Razavi Khorasan, IranTypeTombHistoryPeriodsIlkhanate The Tomb of Abdolabad (Persian: آرامگاه عبدلآباد) is a historical tomb and chahartaqi of Ilkhanate era in Abdolabad village at Bardaskan County.The tomb was added to the list of National Monuments of Iran as the 10,908th monument.[1] Gallery Abdolabad Mosq...

Pour les articles homonymes, voir Douze-Novembre. Éphémérides Novembre 1er 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 12 octobre 12 décembre Chronologies thématiques Croisades Ferroviaires Sports Disney Anarchisme Catholicisme Abréviations / Voir aussi (° 1852) = né en 1852 († 1885) = mort en 1885 a.s. = calendrier julien n.s. = calendrier grégorien Calendrier Calendrier perpétuel Liste de calendriers Naissanc...

Town in Chubut, ArgentinaTrevelin TrefelinTownA winter day in TrevelinTrevelinLocation of Trevelin in ArgentinaCoordinates: 43°5′S 71°28′W / 43.083°S 71.467°W / -43.083; -71.467Country ArgentinaProvince ChubutDepartmentFutaleufúElevation385 m (1,263 ft)Population (2011) • Total9,123Time zoneUTC−3 (ART)CPA baseU9203Dialing code+54 2945ClimateCsbWebsitewww.trevelin.gob.ar Trevelin (Spanish pronunciation: [tɾeˈβel...
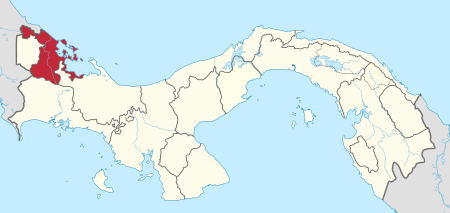
Questa voce o sezione sull'argomento Panama non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Province, comarche e sottoprovince di Panama Le province di Panama costituiscono la suddivisione di primo livello del Paese e sono in tutto dieci; ad esse sono equiordinate tre comarche (comarcas indígenas), mentre altre due comarche rappresentano suddivisioni di...

American politician (1879-1955) Fred H. Brown2nd Comptroller General of the United StatesIn officeApril 11, 1939 – June 19, 1940PresidentFranklin D. RooseveltPreceded byJohn R. McCarlSucceeded byLindsay Carter WarrenUnited States Senatorfrom New HampshireIn officeMarch 4, 1933 – January 3, 1939Preceded byGeorge H. MosesSucceeded byCharles W. Tobey59th Governor of New HampshireIn officeJanuary 4, 1923 – January 1, 1925Preceded byAlbert O. BrownSucceeded...

提示:此条目页的主题不是沙菲宜阿都拉。 这是马来族人名,“阿达”是父名,不是姓氏,提及此人时应以其自身的名“莫哈末·沙菲益”为主。 尊敬的拿督斯里哈芝沙菲益阿达Mohd Shafie bin Hj. Apdal国会议员、州议员马来西亚国会下议院仙本那现任就任日期1995年4月26日前任山卡兰丹戴(馬來語:Sakaran Dandai)(国阵巫统)多数票12,218(1995)13,325(1999)13,319(2004)17,...

College football gameNavy snaps 43-year losing streakNon-conference game Navy Midshipmen Notre Dame Fighting Irish (4–4) (1–7) 46 44 Head coach: Paul Johnson Head coach: Charlie Weis 1234OT2OT3OT Total Navy 01468738 46 Notre Dame 71407736 44 DateNovember 3, 2007Season2007StadiumNotre Dame StadiumLocationSouth Bend, Indiana, U.S.National anthemBand of the Fighting IrishHalftime showBand of the Fighting IrishAttendance80,795United States TV coverageNetworkNBCAnnouncersT...

SMK Sumber Permata BangsaInformasiDidirikan06 Agustus 2012JenisSwastaAkreditasiBNomor Pokok Sekolah Nasional60726520Kepala SekolahDrs. Sari BudisitoJumlah kelas12 kelasJurusan atau peminatanTeknnik Komputer Jaringan dan Teknik Kendaraan Ringan OtomotifKurikulum2013 dan MerdekaJumlah siswa450StatusSMK SwastaAlamatLokasiJL. Kemuning Raya, Bojong Menteng Rawa Lumbu, Cipendawa Lama No. 8 RT. 03 RW. 05, Kel. Bojong Menteng, Kec. Rawalumbu, Kota Bekasi, Jawa Barat 17117, Bekasi, Jawa...

النعمان بن بشير تخطيط اسم الصَّحابي النُّعمان بن بشير ملحوقًا بالترضي عنه - -. معلومات شخصية الميلاد 1 هـالمدينة المنورة الوفاة 65 هـ (65 سنة).حمص سبب الوفاة اغتيال مواطنة الدولة الأموية الأولاد عمرة بنت النعمانحميدة بنت النعمانهند بنت النعمان بن بشير الأب بشير ب...

حسابات قوميةصنف فرعي من محاسبة جزء من الاقتصاد تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولاقتصاد تاريخأفرع تاريخ الاقتصاد مدارس الاقتصاد اقتصاد سائد اقتصاد بدعي المنهجية الاقتصادية اقتصاد سياسي الاقتصاد الجزئي الاقتصاد الكلي اقتصاد دولي اقتصاد تطبيقي...

Canadian politician (1950–2020) Michel GauthierLeader of the OppositionIn officeFebruary 17, 1996 – March 14, 1997Preceded byGilles DuceppeSucceeded byGilles DuceppeLeader of the Bloc QuébécoisIn officeFebruary 17, 1996 – March 14, 1997Preceded byGilles Duceppe (interim)Succeeded byGilles DuceppeMember of Parliamentfor Roberval—Lac-Saint-JeanIn officeJanuary 17, 1994 – July 29, 2007Preceded byBenoit BouchardSucceeded byDenis LebelMember of the Quebec Nat...

Swedish national team, for the Paralympic sport of goalball Sweden women's national goalball teamSwedish women's goalball team throwing, Copper Box, London Paralympic Games (September 2012)SportGoalballLeagueIBSADivisionWomenRegionIBSA EuropeLocationSwedenColoursBlue, yellow ChampionshipsParalympic Games medals: : 0 : 0 : 1 World Championship medals: : 0 : 0 : 0Parent groupSvenska parasportförbundetWebsitewww.parasport.se Sweden women's national goalball team is the women's nati...

Informasi yang dinyatakan dalam kode ASCII untuk kata Wikipedia Informasi[1] atau embaran[2] adalah pesan (ucapan atau ekspresi) atau kumpulan pesan yang terdiri dari order sekuens dari simbol, atau makna yang dapat ditafsirkan dari pesan atau kumpulan pesan. Informasi dapat direkam atau ditransmisikan. Hal ini dapat dicatat sebagai tanda-tanda, atau sebagai sinyal berdasarkan gelombang. Informasi adalah jenis acara yang memengaruhi suatu negara dari sistem dinamis. Para konse...

Daigunder爆闘宣言ダイガンダー(Bakutō Sengen Daigandā)GenreMecha, Aksi, Komedi Seri animeSutradaraHiroyuki YanoStudioBrains BasePelisensi Animation International Ltd.SaluranasliAnimax (2002)TV Tokyo (2002)Saluran bahasa Inggris JetixTayang 5 April 2002 – 27 Desember 2002Episode39 Portal anime dan manga Daigunder (爆闘宣言ダイガンダーcode: ja is deprecated , Bakutō Sengen Daigandā) adalah serial anime tentang manusia yang menggunakan robot dalam turnamen. Dib...

Location of Onondaga County in New York Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) This is a list of the properties and districts listed on the National Register of Historic Places listings in Onondaga County, New York. The locations of National Register properties and districts (at least for all showing latitude and longitude coordinates below) may be seen in a map by clicking on Map of all...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Final Piala Winners Eropa 1972 – berita · surat kabar · buku · cendekiawan · JSTOR Final Piala Winners Eropa 1972TurnamenPiala Winners Eropa 1971–1972 Rangers Dynamo Moscow 3 2 Tanggal24 Mei 1972Stadio...

























![{\displaystyle u(x,t)=-2\nu {\frac {\partial }{\partial x}}\ln \left\{(4\pi \nu t)^{-1/2}\int _{-\infty }^{\infty }\exp \left[-{\frac {(x-x')^{2}}{4\nu t}}-{\frac {1}{2\nu }}\int _{0}^{x'}f(x'')dx''\right]dx'\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c946a41e496bc7244b0dd06c8ab232998984f6e9)






