Divisores binómicos

No debe confundirse con divisiones binarias.

ax^{3}+bx^{2}+cx+d

Forma más común
de divisores binómicos.

Es un método avanzado de factorización que se usa mayormente en los temas de fracciones algebraicas^[1] para este tema es indispensable saber la regla de Ruffini. Su proceso consiste en los siguientes pasos. (Solo funciona en el caso de tener al menos una raíz en ℚ)

Posibles ceros

En este primer paso, los posibles ceros resultan del cociente de la división de los divisores del término independiente^[2] entre los divisores del coeficiente principal^[3] y se dividen uno por uno.
Nota: Para un mejor entendimiento, este método se explicara con el siguiente ejemplo.

Si el enunciado es este:

x^{3}+x^{2}-5x-6

Se ve que el término independiente es 6 y el coeficiente principal es 1. Para sacar los posibles ceros se procede de la siguiente manera:

Pc={\frac {\pm (1,2,3,6)}{\pm (1)}}=\pm (1,2,3,6)

Donde se puede notar que como se mencionó anteriormente cada divisor de arriba fue divido por el de abajo; es decir, que el uno se dividió entre uno; el dos se dividió entre uno; el tres se dividió entre uno y por último el seis se dividió entre uno.

Ruffini (división algebraica)

Ahora se divide por regla de Ruffini, donde se toma como dividendo los coeficientes del enunciado y como divisor los posibles ceros y se prueba con la regla de Ruffini hasta que salga la división exacta (es decir de residuo cero).

{\begin{array}{r|rrrr}&1&1&-5&-6\\-2&&-2&2&6\\\hline &1&-1&-3&0\\&{\text{Coef.}}&&&{\text{Resto}}\end{array}}

Se puede notar que al probar con menos dos, la división salió exacta.

Dos términos

Ahora, nuestra respuesta consta de 2 términos

Primer término

El -2 salió de un x+2 porque si x+2=0, saldría x=-2 . eso quiere decir que nuestro primer término es x+2
Nota: Siempre se iguala a cero y siempre los primeros términos son de la forma x+a .

Segundo término

El segundo término es el coeficiente de nuestra división porsuma , es decir, el segundo término es x²-x-3 .
Nota: En el segundo término, a veces todavía se puede descomponer por aspa simple; si ese es el caso, se debe descomponer.

Resultado final

El resultado final es el siguiente:

(x+2)(x^{2}-x-3)

Nota: Se debe dejar así, no se debe multiplicar, puesto que eso sería retroceder todos los pasos.

Referencias

↑ Son exactamente de la misma forma que las fracciones de Aritmética pero en vez de usar números se usan variables.
↑ Término del polinomio que no está acompañado de una variable.
↑ Coeficiente que está acompañado de la variable de mayor exponente.

Enlaces externos

Matemática1 - factorización - divisores binómicos

Véase también

Datos: Q5811828

Read other articles:

Bahasa Karachai-Balkar

Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman bahasa acak Bahasa Karachai-Balkar Къарачай-Малкъар тилТаулу тил Dituturkan di Rusia WilayahKabardino-BalkariaKarachay-CherkessiaEtnisKarachai, BalkarPenuturRincian data penutur Jumlah penutur beserta (jika ada) metode pengambilan, jenis, tanggal, dan tempat.[1][2] 305.364 (Rusia, 2010)310.400 (2010) Ru...

Avignon

Avignon Lambang kebesaranAvignon Lokasi di Region Provence-A.-C.d'A. Avignon Koordinat: 43°57′N 4°49′E / 43.95°N 4.81°E / 43.95; 4.81NegaraPrancisRegionProvence-Alpes-Côte d'AzurDepartemenVaucluseArondisemenAvignonAntarkomuneGrand AvignonPemerintahan • Wali kota (2008–2014) Marie-Josée Roig (UMP)Luas • Land164,78 km2 (2,501 sq mi) • Populasi294.787 • Kepadatan Populasi215/km2 (38/sq mi)Zona...

ISO basic Latin alphabet

26 letters in two cases broadly used in international communication The ISO basic Latin alphabet is an international standard (beginning with ISO/IEC 646) for a Latin-script alphabet that consists of two sets (uppercase and lowercase) of 26 letters, codified in[1] various national and international standards and used widely in international communication. They are the same letters that comprise the current English alphabet. Since medieval times, they are also the same letters of the ...

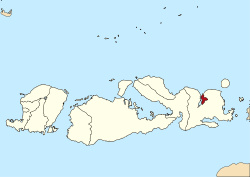
Daftar kecamatan dan kelurahan di Kota Bima

Peta Lokasi Kota Bima di Nusa Tenggara Barat Berikut adalah Daftar kecamatan dan kelurahan/desa di Kota Bima, Provinsi Nusa Tenggara Barat, Indonesia. Kota Bima terdiri dari 5 Kecamatan dan 41 Kelurahan. Pada tahun 2017, jumlah penduduknya mencapai 141.294 jiwa dengan luas wilayah 222,25 km² dan sebaran penduduk 635jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kota Bima, adalah sebagai berikut: Kemendagri Kecamatan Jumlah Kelurahan Daftar Kelurahan 52.72.03 Asakota 6 Jat...

Mesosphere

Layer of the atmosphere directly above the stratosphere and below the thermosphere This article is about the atmospheric layer. For other uses, see Mesosphere (disambiguation). Earth's atmosphere as it appears from space, as bands of different colours at the horizon. From the bottom, afterglow illuminates the troposphere in orange with silhouettes of clouds, and the stratosphere in white and blue. Next the mesosphere (pink area) extends to just below the edge of space at one hundred kilometer...

Russia Sanctions Act 2022

Act of Parliament in New Zealand Russia Sanctions Act 2022New Zealand ParliamentRoyal assent11 March 2022[1]Legislative historyIntroduced byNanaia Mahuta[1]First reading9 March 2022[1]Second reading9 March 2022[1]Third reading9 March 2022[1]Status: Current legislation The Russia Sanctions Act 2022 is an Act of Parliament passed by the New Zealand Parliament that establishes the framework for autonomous sanctions against Russia in response to its 2022 in...

1922 Penn State Nittany Lions football team

American college football season 1922 Penn State Nittany Lions footballRose Bowl, L 3–14 vs. USCConferenceIndependentRecord6–4–1Head coachHugo Bezdek (5th season)CaptainNewsh BentzHome stadiumNew Beaver FieldUniformSeasons← 19211923 → 1922 Eastern college football independents records vte Conf Overall Team W L T W L T Cornell – 8 – 0 – 0 Princeton – 8 – 0 – 0 Army ...

Paul Theroux

Questa voce o sezione sull'argomento scrittori statunitensi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Paul Theroux Paul Theroux (Medford, 10 aprile 1941) è uno scrittore statunitense. Indice 1 Biografia 2 Opere 2.1 Narrativa 2.2 Saggistica 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Th...

Actinolepis (placoderm)

Extinct genus of fishes Not to be confused with Actinolepis (plant). ActinolepisTemporal range: Early Devonian, 409.1–391.9 Ma PreꞒ Ꞓ O S D C P T J K Pg N Reconstruction of A. tuberculata Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: †Placodermi Order: †Arthrodira Family: †Actinolepidae Genus: †ActinolepisAgassiz, 1845[1] Type species †Actinolepis tuberculataAgassiz, 1845[1] Other species †A. magna Mark-Kurik, 1973...

زابرودي (فورونيز)

زابرودي تقسيم إداري البلد روسيا تعديل مصدري - تعديل يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) زابرودي (بالروسية: Заброды) هي مدينة في مقاطع...

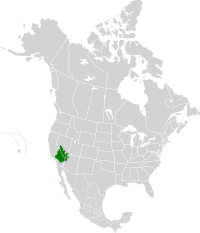
Mojave Desert

Desert in the southwestern United States Mojave DesertHayyikwiir Mat'aar (Mohave)Desierto de Mojave (Spanish)Sand dunes in Death ValleyLocation within North AmericaEcologyRealmNearcticBiomeDeserts and xeric shrublandsBorders List California montane chaparral and woodlandsColorado Plateau shrublandsGreat Basin DesertSonoran DesertSierra Nevada Bird species230[1]Mammal species98[1]GeographyArea81,000 km2 (31,000 sq mi)CountryUnited StatesStatesArizonaCal...

Orthetrum julia

Species of dragonfly Orthetrum julia Male, uMkhuze Game Reserve, KwaZulu Natal, South Africa Female, Ithala Game Reserve, KwaZulu Natal, South Africa Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Odonata Infraorder: Anisoptera Family: Libellulidae Genus: Orthetrum Species: O. julia Binomial name Orthetrum juliaKirby, 1900 Orthetrum julia, the Julia skimmer is a species o...

London Marathon

Annual race held in London, England London MarathonDateAprilLocationLondon, United KingdomEvent typeRoadDistanceMarathonEstablished29 March 1981; 43 years ago (1981-03-29)Course recordsMen: 2:01:25 (Kelvin Kiptum, 2023)Women: 2:15:25 (Paula Radcliffe, 2003)Wheelchair men: 1:23:44 (Marcel Hug, 2023)Wheelchair women: 1:38:24 (Catherine Debrunner, 2022)Official sitewww.tcslondonmarathon.com 2024 London Marathon The London Marathon (also known as the TCS London Marathon for spon...

Religion in Kazakhstan

Religion in Kazakhstan (2023 Census)[1] Islam (mainly Sunni) (74%) Christianity (14%) Atheism (2%) Other or undeclared (11.25%) According to various polls, the majority of Kazakhstan's citizens, primarily ethnic Kazakhs, identify as Sunni Muslims.[2][3] In 2020, Shia Muslims made up 0.55% of the population.[4] According to the estimate by the Pew Research Center, 75% of the population practices the religion of Islam...

Fundamental theorem of arithmetic

Integers have unique prime factorizations Not to be confused with Fundamental theorem of algebra. In Disquisitiones Arithmeticae (1801) Gauss proved the unique factorization theorem [1] and used it to prove the law of quadratic reciprocity.[2] In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up t...

Торбинский, Дмитрий Евгеньевич

Дмитрий Торбинский Общая информация Полное имя Дмитрий Евгеньевич Торбинский Родился 28 апреля 1984(1984-04-28)[1] (40 лет)Норильск, Красноярский край, РСФСР, СССР Гражданство Россия Рост 176[2] см Позиция полузащитник Молодёжные клубы ДЮСШ (Норильск)[3] 1996—2002 Спарта�...

Udmurts

Permian ethnic group of Udmurtia, Russia Ethnic group Udmurts УдмуртъёсFlag of UdmurtiaUdmurt children wearing traditional outifits during a flower festival in Igrinsky, Udmurtia, Russia (2019)Total population396,000 (2021)Regions with significant populationsUdmurtia Russia386,465 (2021) Kazakhstan5,824 (2009) Ukraine4,712 (2001)[1] Estonia193 (2011)[2] Latvia179 - 197 (2023)[3][4]LanguagesUdmurt, RussianReligionMajority: Russi...

Oster conspiracy

Proposed plan to overthrow Adolf Hitler Hans Oster in 1939 The Oster Conspiracy (German: Septemberverschwörung, lit. 'September Conspiracy') of 1938 was a proposed plan to overthrow German Führer Adolf Hitler and the Nazi regime if Germany went to war with Czechoslovakia over the Sudetenland. It was led by Generalmajor Hans Oster, deputy head of the Abwehr, and other high-ranking conservatives within the Wehrmacht who opposed the regime for behavior that was threatening to bri...

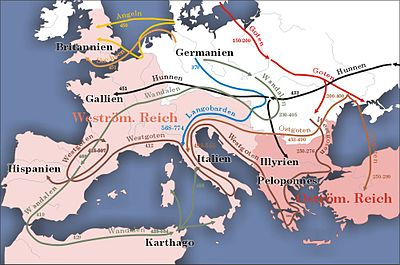
アラリック1世

「アラリック」はこの項目へ転送されています。5世紀末から6世紀初頭の西ゴート王については「アラリック2世」をご覧ください。アラリック1世𐌰𐌻𐌰𐍂𐌴𐌹𐌺𐍃Alaric I 西ゴート国王 395年にアテネを占領したアラリック1世在位 395年 - 410年出生 370/75年ドブロジャ死去 410年コゼンツァ埋葬カラブリア配偶者アタウルフの姉妹子女（庶子または義理の子）テオド�...

Mesogeia Painter

Unidentified ancient Greek vase painter Early Proto-Attic hydria by the Mesogeia Painter, note applied plastic snakes on lip, neck and handle, suggesting a use in funerary cult; neck depicts women dancing with a youth, belly a man behind two sphinxes, circa 700 BC, from Athens, now Antikensammlung, Berlin. The Mesogeia Painter, also Mesogaia Painter, was an Early Proto-Attic vase painter. His conventional name is derived from his name vases, several hydriai decorated by him and discovered in ...