Distribución de Dirichlet
|
Read other articles:
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Bilangan Suzhou – berita · surat kabar · buku · cendekiawan · JSTOR (July 2009) Suzhou numerals Hanzi tradisional: 蘇州碼子 Hanzi sederhana: 苏州码子 Alih aksara Mandarin - Hanyu Pinyin: sūzhōu mǎz...

Untuk kegunaan lain, lihat Benjamin Schwarz (disambiguasi). Ben SchwartzSchwartz pada 2019LahirBenjamin Schwartz15 September 1981 (umur 42)The Bronx, New York, Amerika SerikatPekerjaanPemeranpelawakpenulissutradaraproduserTahun aktif2006–kiniKarier komediMediaFilm, televisi, internetGenreKomedi improvisasionalSitus webwww.rejectedjokes.com Benjamin Schwartz (lahir 15 September 1981)[1] adalah seorang pemeran, pelawak, penulis, sutradara dan produser Amerika Serikat, yang m...

Australian politician This article is about the Australian politician. For other people with the same name, see Malcolm Roberts. SenatorMalcolm RobertsRoberts in Blackwater in October 2020Senator for QueenslandIncumbentAssumed office 1 July 2019Preceded byFraser AnningIn office2 July 2016 (2016-07-02) – 27 October 2017 (2017-10-27)Succeeded byFraser Anning Personal detailsBornMalcolm Ieuan Roberts (1955-05-03) 3 May 1955 (age 68)[1]Dis...

Pékin 2008 Généralités Sport Football Édition 22e Lieu(x) Pékin Date 6 au 23 août 2008 Participants Hommes : 16 équipesFemmes : 12 équipes Épreuves 2 Site(s) Stade de Shanghai Stade des ouvriers Centre olympique Stade de Shenyang Stade de Qinhuangdao finales : Stade national Palmarès Tenant du titre : Argentine : États-Unis Vainqueur : Argentine (2) : États-Unis (3) Navigation Athènes 2004 Londres 2012 modifier Les compétitions de football ...

Cesare BeccariaMarchese di Gualdrasco e di VillareggioStemma In carica1782 –1794 PredecessoreGiovanni Saverio Beccaria SuccessoreGiulio III Beccaria NascitaMilano, 15 marzo 1738 MorteMilano, 28 novembre 1794 (56 anni) SepolturaCimitero della Mojazza DinastiaBeccaria-Bonesana PadreGiovanni Saverio Beccaria MadreMaria Visconti di Saliceto ConiugiTeresa BlascoAnna Barbò FigliGiuliaMariaGiovanni AnnibaleMargheritaGiulio ReligioneCattolicesimo «Se dimostrerò non essere la mort...

Мастер не на все рукиангл. Master of None Жанр комедия-драма Создатели Азиз АнсариАлан Янг В главных ролях Азиз АнсариНоэль УэллсЭрик ВерхеймКельвин ЮЛина УэйтАлессандра Мастронарди Страна США Язык английский[1] Число сезонов 3 Число серий 25 (список серий[d]) Про�...

Medical specialty dealing with disorders of the nervous system This article is about the branch of medicine. For the scientific study of the nervous system, see Neuroscience. For the journal, see Neurology (journal). Neurological sciences redirects here. For the journal, see Neurological Sciences (journal). This scientific article needs additional citations to secondary or tertiary sources such as review articles, monographs, or textbooks. Please also establish the relevance for any primary r...

Religious and political movement that established the Church of Scotland Statue of John Knox, a leading figure of the Scottish Reformation. Part of a series on theReformationNinety-five Theses, written by Martin Luther in 1517 Precursors Peter Waldo and Waldensians John Wycliffe and Lollardy Jan Hus and Hussites Girolamo Savonarola and Piagnoni Arnold of Brescia and Arnoldists Gottschalk of Orbais Ratramnus Claudius of Turin Berengar of Tours and Berengarians Wessel Gansfort Johann Ruchrat vo...

Pour les articles homonymes, voir Wisconsin (homonymie). Wisconsin Sceau du Wisconsin. Drapeau du Wisconsin. Carte des États-Unis avec le Wisconsin en rouge.SurnomBadger State, America's DairylandEn français : « l’État du blaireau », « le pays-laitier des États-Unis ».DeviseForward« En avant ». Administration Pays États-Unis Capitale Madison Adhésion à l’Union 29 mai 1848 (175 ans) (30e État) Gouverneur Tony Evers (D) Sénateurs ...

Virginia Slims of California 1986 Sport Tennis Data 24 febbraio - 2 marzo Edizione 16a Superficie Sintetico indoor Campioni Singolare Chris Evert-Lloyd Doppio Hana Mandlíková / Wendy Turnbull 1985 1987 Il Virginia Slims of California 1986 è stato un torneo di tennis giocato sul sintetico indoor. È stata la 16ª edizione del torneo, che fa parte del Virginia Slims World Championship Series 1986. Si è giocato a San Francisco negli Stati Uniti, dal 24 febbraio al 2 marzo 1986. Indice 1 Cam...

Negationist myth of the American Civil War Lost Cause redirects here. For other uses, see Lost Cause (disambiguation). Custis Lee (1832–1913) rode on horseback in front of the Jefferson Davis Memorial in Richmond, Virginia on June 3, 1907, reviewing the Confederate Reunion Parade. The Lost Cause of the Confederacy (or simply the Lost Cause) is an American pseudohistorical[1][2] and historical negationist myth[3][4][5] that claims the cause of the Conf...

Kingdom of ancient India This article is about the Mahabharata epic kingdom of Panchala. For the historical kingdom, see Panchala. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Pa...

Manœuvre d'un bateau à abattre. Cet article est une ébauche concernant la voile ou un voilier. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Vaisseau de ligne abattant pour appareiller. Sur un voilier, abattre c'est manœuvrer le bateau de manière à l'écarter du lit du vent. Description Pour abattre, le barreur (ou le timonier) modifie le cap suivi en agissant sur la barre. Comme dans toute manœuvre modi...

Baseball umpire, Olympic Games official Riccardo FraccariPresident of the WBSCIncumbentAssumed office 10 May 2014President of the IBAFIn office6 December 2009 – 10 May 2014Preceded byHarvey SchillerSucceeded byHimself(as president of the WBSC) Personal detailsBorn (1949-05-30) May 30, 1949 (age 74)Pisa, Italy Riccardo Fraccari (born 30 May 1949 in Pisa, Italy) is an international sports administrator who is the current president of the World Baseball Softball Confederation...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Cet article est une ébauche concernant une localité allemande. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Simbach am Inn L'hôtel de ville de Simbach am Inn. Armoiries Administration Pays Allemagne Land Bavière District(Regierungsbezirk) Basse-Bavière Arrondissement(Landkreis) Rottal-Inn Bourgmestre(Bürgermeister) Günther Wöhl Code postal 84359 Code communal(Gemeindeschlüssel) 09 2 77 145 Indicatif ...

Metro HanoiInfoWilayahHanoi, VietnamJenisAngkutan cepatJumlah jalur1 (beroperasi)1 (dalam pembangunan)Jumlah stasiun12 (beroperasi)12 (dalam pembangunan)Penumpang harian32.000 (2023)Penumpang tahunan10,7 juta (2023)Situs webhanoimetro.net.vn/enOperasiDimulai6 November 2021OperatorPerusahaan Metro Hanoi dan Metro TokyoJumlah gerbong13TeknisPanjang sistem13,1 km (beroperasi)12 km (dalam pembangunan)Lebar sepur1.435 mm (4 ft 8+1⁄2 in)(sepur standar)ListrikRel ketiga 750...
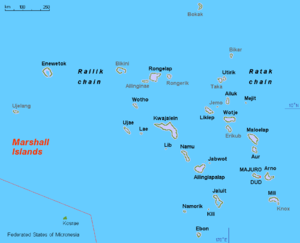
Peta kepulauan Ralik dan Ratak Ralik adalah salah satu dari dua kepulauan di Kepulauan Marshall yang terletak di sebelah barat dari kepulauan yang lain, yaitu Ratak. Dalam bahasa Marshall, ralik berarti 'matahari terbenam'.[1] Pada tahun 2011, populasi total penduduk di kepulauan ini adalah 19.257 jiwa.[2] Atol dan pulau Atol Ailinginae Atol Ailinglaplap Atol Bikini Atol Ebon Atol Enewetak Atol Jaluit Atol Kwajalein Atol Lae Atol Namdrik Atol Namu Atol Rongdrik Atol Rongelap A...

第三十一届夏季奧林匹克運動會男子5000米比賽摄于比赛结束后比賽場館阿維蘭熱奧林匹克體育場日期2016年8月17日(预赛)2016年8月20日(决赛)参赛选手51位選手,來自28個國家和地區冠军成绩13:03.30奖牌获得者01 ! 莫·法拉赫 英国02 ! 保罗·切里莫 美国03 ! 哈格斯·葛布里维特 埃塞俄比亚← 20122020 → 2016年夏季奧林匹克運動會田徑比賽 徑賽...

تشارلز ناثانيل هاسكل معلومات شخصية الميلاد 13 مارس 1860(1860-03-13)لايبسيك، أوهايو الوفاة 5 يوليو 1933 (73 سنة)أوكلاهوما سيتي، أوكلاهوما سبب الوفاة ذات الرئة مكان الدفن موسكوغي مواطنة الولايات المتحدة مناصب حاكم أوكلاهوما في المنصب16 نوفمبر 1907 – 9 يناير 1911 لي �...
















