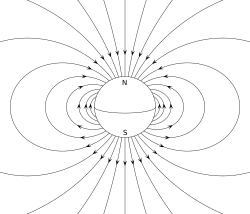
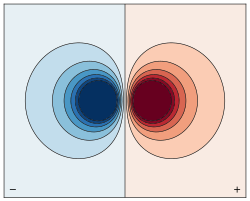
Dipolo eléctrico
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Maria MutolaMutola, 2008Informasi pribadiJulukanMaputo Express,[1] LurdinhaKewarganegaraanMozambicanLahir27 Oktober 1972 (umur 51)Lourenço Marques, MozambiqueTinggi165 m (541 ft 4 in)Berat63 kg (139 pon) (139 pon...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Gonadal artery – news · newspapers · books · scholar · JSTOR (February 2024) Gonadal arteryThe abdominal aorta and its branches.DetailsSourceabdominal aortaVeingonadal veinSuppliesgonadsAnatomical terminology[edit on Wikidata] The term gonadal art...

HFI - Himpunan Fisika Indonesia (Indonesian Physical Society - IPS),adalah organisasi profesi ilmiah untuk bidang FISIKA yang telah berdiri sejak 17 Agustus 1973. Pranala luar Situs resmi HFI Artikel bertopik organisasi ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

American video game developer For the Malaysian mobile telecommunications company, see Maxis Communications. Not to be confused with Maxxis. MaxisMaxis logo used since 2022Company typeDivisionIndustryVideo gamesFounded1987; 37 years ago (1987)FoundersWill WrightJeff BraunHeadquartersRedwood City, California, USKey peopleCatharina Lavers Mallet[1](general manager)ProductsThe Sims series (2000–present)SimCity series (1989–2014)Sim series (1989–2010)Spore (2008)Da...

Head of the Chinese Communist Party For a list of leaders of the Chinese Communist Party, see Leader of the Chinese Communist Party.Not to be confused with Secretary-general of the Chinese Communist Party. General Secretary of theCentral Committee of the Chinese Communist Party中国共产党中央委员会总书记Emblem of the Chinese Communist PartyFlag of the Chinese Communist PartyIncumbentXi Jinpingsince 15 November 2012Central Committee of the Chinese Communist PartySecretariat of...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يمتد تاريخ الاستيطان البشري في منطقة الأنديز في أمريكا الجنوبية من نحو 15000 قبل الميلاد إلى يومنا هذا. تتضمن المنطقة الممتدة على 7000 كيلومتر طولًا (4300 ميل) بيئات جبلية واستوائية...

Kenyon's voice recorded 2012, as part of an audio description of Postman's Park for VocalEyes Problems playing this file? See media help. Sir Nicholas Roger Kenyon, CBE (born 23 February 1951, Cheshire), is a British music administrator, editor and writer on music. Responsible for the BBC Proms 1996–2007, he was then appointed Managing Director of the Barbican Centre, before stepping down in September 2021 to become opera critic of The Telegraph and a Visiting Scholar in the Faculty of Mus...

Unofficial title of wife of the President of Israel First Lady of IsraelIncumbentMichal Herzogsince 7 July 2021ResidenceBeit HaNassiAppointerKnessetInaugural holderVera WeizmannFormation17 February 1949 First Lady of Israel is the unofficial title of the wife of the president of Israel. The current first lady of Israel is Michal Herzog, wife of President Isaac Herzog. History There is no official role or office of the first lady of Israel,[1] although President Reuven Rivlin best...

For the baseball player, see Joe Nathan. GlaxoSmithKline global headquartersBrentford, London 2011 Wellington headquarters opened 1874 new building, same Wellington site, opened 1907 Joseph Edward Nathan (1835 – 2 May 1912) was a London-born New Zealand merchant, dairy manufacturer and exporter. A successful businessman, he returned to London in 1887 after 30 years in New Zealand. The business he founded has become GlaxoSmithKline, as of 2015 the world's seventh largest pharmaceutical comp...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

Ye Olde Fighting Cocks in St Albans, Hertfordshire holds the Guinness World Record for the oldest pub in England. This is an index of drinking establishment-related articles. Contents A B C D E F G H I J K L M N O P Q R S T U V W X Y Z See also References External links Bartenders at the St. Charles Hotel in Toronto, circa 1911 Types of drinking establishment Alcohol-free bar Australian pub Bar Beer hall Biker bar Bloodhouse Botequim Brewpub Cantina Cider house Cigar bar Dance bar Desi pub D...

State park in Oregon, United States D River State Recreation SiteShow map of OregonShow map of the United StatesTypePublic, stateLocationLincoln County, OregonNearest cityLincoln CityCoordinates44°58′01″N 124°01′04″W / 44.967053°N 124.0178914°W / 44.967053; -124.0178914[1]Operated byOregon Parks and Recreation Department D River State Recreation Site (also D River State Wayside[2] and D River State Park[1]) is a state park ...

Moulmein beralih ke halaman ini. Untuk kegunaan lain, lihat Moulmein (disambiguasi). Mawlamyine မော်လမြိုင်မြို့MawlamyineLetak Mawlamyine, Myanmar (Burma)Koordinat: 16°29′N 97°37′E / 16.483°N 97.617°E / 16.483; 97.617Negara Myanmar (Burma)Negara bagianMonDistrikMawlamyineKotaprajaMawlamyinePopulasi (Sensus 2014)[1] • Kota289.388 • Perkotaan253.734 • Rural35.654 • ...

Polybutylene terephthalate Names IUPAC name Poly(oxy-1,4-butanediyloxycarbonyl-1,4-phenylenecarbonyl) Identifiers CAS Number 24968-12-5 Y ChemSpider none Properties[1] Chemical formula (C12H12O4)n Melting point 223 °C (433 °F; 496 K) Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa). N verify (what is YN ?) Infobox references Chemical compound Polybutylene ter...

Badminton competition Men's singles WH1at the XVI Paralympic GamesVenueYoyogi National GymnasiumDates1–4 September 2021Competitors9 from 6 nationsMedalists Qu Zimo China Lee Sam-seop South Korea Lee Dong-seop South Korea2024→ Badminton at the2020 Summer ParalympicsQualificationSinglesMenWomenWH1WH1WH2WH2SL3SL4SL4SU5SU5SH6DoublesMenWomenWH1–WH2WH1–WH2SL3–SU5MixedSL3–SU5vte The men's singles WH1 tournament at the 2020 Summer Paralympics in Tokyo took plac...

Barisan Islam Pan-Malaysia Barisan Jemaah Islamiah Se-MalaysiaNama dalam bahasa InggrisPan-Malaysian Islamic FrontNama dalam bahasa MelayuBarisan Jemaah Islamiah Se-Malaysia (BERJASA)باريسن جماعه اسلاميه سمليسياSingkatanBERJASA / برجاساKetua umumProf Dato' Dr Badhrulhisham Abdul AzizDibentuk23 Desember 1977Dipisah dariPartai Islam Se-MalaysiaKantor pusatPasir Mas, Kelantan, MalaysiaSayap pemudaAngkatan Pemuda-Pemudi BERJASA (ANGKASA)Sayap wanitaWanita BERJA...

Itzik Feffer, Albert Einstein und Solomon Michailowitsch Michoels Itzik Feffer (auch Fefer, jiddisch איציק פֿעפֿער, russisch Ицик Фефер, Исаак Соломонович Фефер; geboren 10. September 1900 in Schpola, Gouvernement Kiew, Russisches Kaiserreich; gestorben 12. August 1952 in Moskau) war ein sowjetischer jiddischer Autor. Er wurde 1952 ein Opfer der Stalinschen Säuberungen. Feffer war zunächst Mitglied des Bund und wurde 1919 Mitglied der KPR(B). 1920 v...

Former shore establishment of the Royal Navy For other ships with the same name, see HMS Dolphin. Davis Submerged Escape Apparatus training at HMS Dolphin The seventeenth Royal Navy vessel to be named HMS Dolphin was the Royal Naval shore establishment sited at Fort Blockhouse in Gosport. Dolphin was the home of the Royal Navy Submarine Service from 1904 to 1999, and location of the Royal Navy Submarine School. Closure of submarine base The blockhouse and fortifications of the site had been c...
この記事で示されている出典について、該当する記述が具体的にその文献の何ページあるいはどの章節にあるのか、特定が求められています。 ご存知の方は加筆をお願いします。(2022年8月) 猪谷駅 駅舎外観(2019年5月) いのたに Inotani ◄**杉原 (8.7 km) (7.0 km) 楡原**► 所在地 富山県富山市猪谷字旦暮1085北緯36度28分18.16秒 東経137度14分17.04秒 / �...

Contea di NolanconteaContea di Nolan – VedutaTribunale della contea LocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoSweetwater Data di istituzione1876 TerritorioCoordinatedel capoluogo32°18′36″N 100°24′00″W32°18′36″N, 100°24′00″W (Contea di Nolan) Superficie2 367 km² Abitanti15 216 (2010) Densità6,43 ab./km² Altre informazioniLingueinglese Fuso orarioUTC-6 CartografiaSweetwater Contea di Nolan – Mappa Sito istit...

















![{\displaystyle U=\int _{{\theta }_{0}}^{\theta }pE\sin \theta d\theta =pE\int _{{\theta }_{0}}^{\theta }\sin \theta d\theta =-pE[\cos \theta -\cos {\theta }_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8005703742e3aac00c7755ac470e6d3b445ede2d)




![{\displaystyle ={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q[(d\cos \theta -d_{p}){\hat {\mathbf {e} }}_{x}+(d\sin \theta ){\hat {\mathbf {e} }}_{y}]}{[(d\cos \theta -d_{p})^{2}+(d\sin \theta )^{2}]^{3/2}}}-{\frac {q[(d\cos \theta +d_{p}){\hat {\mathbf {e} }}_{x}+(d\sin \theta ){\hat {\mathbf {e} }}_{y}]}{[(d\cos \theta -d_{p})^{2}+(d\sin \theta )^{2}]^{3/2}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb890adbca65eafb4812baa33fd0b2700189118)


![{\displaystyle \mathbf {E} _{dip}\approx {\frac {1}{4\pi \epsilon _{0}}}\left({\frac {-2qd_{p}}{[d^{2}+d_{p}^{2}]^{3/2}}}{\hat {\mathbf {e} }}_{x}+{\frac {6qd^{2}d_{p}\cos(\theta )}{[d^{2}+d_{p}^{2}]^{5/2}}}{\hat {\mathbf {e} }}_{y}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45887f92f50ac97ec1a44490a724103fa92a3380)














