Difeomorfismo
|
Read other articles:
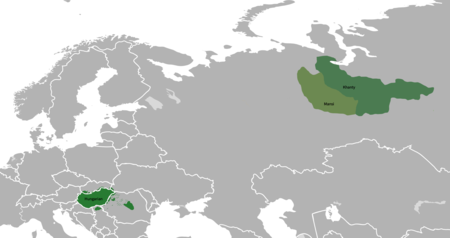
Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Cari berdasarkan nilai Glottolog Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman rumpun acak Rumpun bahasaUgrik (kontroversial) UgrianPersebaranHungaria dan Siberia baratPenggolongan bahasaUralikFinno-UgrikUgrik Bahasa Hungaria Bahasa Khanty Bahasa Mansi Kode bahasaGlottolognoneLokasi penuturanPenyebaran bahasa Ugrik Portal BahasaSunting kotak info • L • B • PWBantuan...

Fazioli PianofortiJenisPerseroan terbatasIndustriInstrumen musikDidirikan1981PendiriPaolo FazioliKantorpusatSacile, ItaliaTokohkunciPaolo FazioliProdukPiano Grand, Piano Grand KonserPendapatan€10.000.000 (2018)Karyawan50 (2018)Situs webwww.fazioli.com Fazioli Pianoforti (pengucapan bahasa Italia: [faˈtsjɔːli]) memproduksi piano grand dan konser di pabriknya di Sacile, Italia dengan tangan. Perusahaan ini didirikan oleh insinyur dan pianis Paolo Fazioli[1] pada tahun 1978. ...

Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland Afrika Selatan ...

Map all coordinates using OSMMap up to 200 coordinates using Bing Export all coordinates as KML Export all coordinates as GeoRSS Export all coordinates as GPX Map all microformatted coordinates Place data as RDF Ang Macerata ngalan niining mga mosunod: Italya 1 2 3 Mga dapit nga gitawag Macerata sa Italya. Provincia di Macerata, lalawigan, Marche, 43°12′00″N 13°10′00″E / 43.2°N 13.16667°E / 43.2; 13.16667 (Provincia di Macerata) Macerata (kapital s...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Protected area in the United States Duxbury Reef State Marine Conservation Area (SMCA) is a marine protected area located about 1 mile (2 km) west of Bolinas in Marin County on California’s north central coast. This marine protected area covers 0.66 square miles (1.7 km2). Duxbury Reef SMCA prohibits the take of all living marine resources, except the recreational take of finfish from shore only and the recreational take of abalone. History Duxbury Reef SMCA is one of 22 marine pr...

Цю статтю потрібно повністю переписати відповідно до стандартів якості Вікіпедії. Ви можете допомогти, переробивши її. Можливо, сторінка обговорення містить зауваження щодо потрібних змін. (вересень 2019) Для загального ознайомлення дивіться статтю «Прийменник». Прий�...

La LunaInformasi latar belakangAsalBandung, IndonesiaGenrePopjazzTahun aktif2000–sekarangLabelBulletinSitus webwww.lalunaband.comAnggotaManik PurwakrishnaUtiBoyanMantan anggotaErwin Januar La Luna (Bahasa Spanyol untuk Sang Rembulan) adalah grup band Indonesia yang didirikan di Bandung, Jawa Barat pada 2 Januari 2000.[1] Grup ini didirikan oleh Manik (vokal), Uti (Gitar), Boyan (drum), dan Erwin (bass). Pada tahun 2000, La Luna merilis debut album Penggalan Kisah Lama dengan single ...

Aspect of Turkish archaeology Below is the list of ancient settlements in Turkey. There are innumerable ruins of ancient settlements spread all over the country. While some ruins date back to Neolithic times, most of them were settlements of Hittites, Phrygians, Lydians, Ionians, Urartians, and so on. List of settlements In the table below, only the settlements which have articles in this encyclopaedia are shown, with the exception of the following: A few ancient settlements are still in use ...

История № 203«Одиннадцатый часThe Eleventh Hour»англ. The Eleventh HourСерия «Доктора Кто» Кульминационная сцена: Доктор разговаривает с Атракси и велит им никогда не возвращаться, так как у Земли есть защитник. Актёры Доктор Мэтт Смит — Одиннадцатый Доктор Спутник Карен Гилла�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2017) جيمس أرثر آرثر خلال توقيع كتابه عام 2013]] معلومات شخصية اسم الولادة (بالإنجليزية: James Andrew Arthur) الميلاد 2 مارس 1988 (36 سنة)[1] ميدلزبرة مواطنة المملك�...

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...

بلد وين الإحداثيات 4°44′09″N 45°12′14″E / 4.7359722222222°N 45.203972222222°E / 4.7359722222222; 45.203972222222 تقسيم إداري البلد الصومال[1] التقسيم الأعلى مقاطعة بلدوين عاصمة لـ هيران خصائص جغرافية المساحة 24 كيلومتر مربع ارتفاع 182 متر معلومات أخرى منطقة زمني...
89th season in franchise history 2013 New York Giants seasonOwnerJohn MaraSteve TischGeneral managerJerry ReeseHead coachTom CoughlinHome fieldMetLife StadiumResultsRecord7–9Division place3rd NFC EastPlayoff finishDid not qualifyPro BowlersS Antrel RolleUniform ← 2012 Giants seasons 2014 → The 2013 New York Giants season was the franchise's 89th season in the National Football League (NFL), the fourth playing their home games at MetLife Stadium and the tenth under...

Pusat kota Kitchener Kitchener merupakan sebuah kota di Kanada. Kota ini merupakan kota terbesar kelima di Provinsi Ontario. Pada tahun 1854 hingga 1912 nama kota ini menjadi Town of Berlin dan 1912 hingga 1916 menjadi City of Berlin. Kota ini terletak di bagian selatan di negara itu. Penduduknya berjumlah 204.668 jiwa (kota). Di wilayah metropolitan, berjumlah 451.235 jiwa (2006). Lihat pula Berlin to Kitchener name change Kitchener City Hall CKCO-TV Pranala luar City of Kitchener Kitchener ...

For related races, see 1930 United States gubernatorial elections. 1930 Connecticut gubernatorial election ← 1928 November 4, 1930 1932 → Nominee Wilbur Lucius Cross Ernest E. Rogers Party Democratic Republican Popular vote 215,072 209,607 Percentage 49.91% 48.64% County resultsCross: 50–60% Rogers: 50–60% Governor before election John H. Trumbull Republican Elected Governor Wilbur Lucius Cross ...

NBA professional basketball team season NBA professional basketball team season 1999–2000 Charlotte Hornets seasonHead coachPaul SilasGeneral managerBob BassOwner(s)George Shinn Ray WooldridgeArenaCharlotte ColiseumResultsRecord49–33 (.598)PlaceDivision: 2nd (Central)Conference: 4th (Eastern)Playoff finishFirst round(lost to 76ers 1–3)Stats at Basketball-Reference.comLocal mediaTelevision SportSouth WJZY RadioWBT < 1998–99 2000–01 > Players warming up prior ...

Кубок Хопмана — ежегодный традиционный выставочный теннисный турнир, задуманный, организованный и впервые проведённый Полом Макнами и Чарли Фанкаттом, проходивший в Перте, Западная Австралия, на рубеже декабря и января. Содержание 1 Формат 2 Место проведения 3 Гарри Х...

Radio station in Salladasburg, PennsylvaniaWBYLSalladasburg, PennsylvaniaBroadcast areaWilliamsport, PennsylvaniaFrequency95.5 MHzBrandingBill 95ProgrammingFormatCountryAffiliationsPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsWBLJ-FM, WKSB, WRAK, WRKK, WVRT, WVRZHistoryFirst air date1983Former call signsWKHL-FM (1990–1992)WMRE-FM (1992–1995)WRAK-FM (1995–1996)WMYL (1996–2000)Call sign meaningBYL sounds like BillTechnical information[1]Licen...

КоммунаТажанTajan Герб 43°11′21″ с. ш. 0°27′38″ в. д.HGЯO Страна Франция Регион Юг — Пиренеи Департамент Верхние Пиренеи Кантон Ланнемезан Мэр Андре Рекюр(2014—2020) История и география Площадь 4,93 км² Высота центра 394–564 м Часовой пояс UTC+1:00, летом UTC+2:00 Население Населе...


























