Desigualdad de Cauchy-Bunyakovsky-Schwarz
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Andronik KaragezyanInformasi pribadiNama lengkap Andronik Arutyunovich KaragezyanTanggal lahir 17 Desember 1974 (umur 49)Tempat lahir Gulkevichi, Krasnodar Krai, RusiaTinggi 195 m (639 ft 9 in)Posisi bermain Penjaga gawangKarier se...

2007 video game For the games at a carnival, see Carnival game. 2007 video gameCarnival GamesNorth American Wii box artDeveloper(s)Cat Daddy GamesPublisher(s)Global Star Software (Wii)2K (DS, iPhone)Platform(s)Wii, Nintendo DS, iOS (iPhone)ReleaseWiiNA: August 27, 2007AU: October 19, 2007EU: October 26, 2007DSNA: July 8, 2008EU: August 22, 2008AU: September 4, 2008iPhoneAugust 5, 2010Genre(s)PartyMode(s)Single-player, multiplayer Carnival Games (known in Europe and Australia as Carnival Funfa...

Untuk kegunaan lain, lihat Frankfurt. Frankfurter Rundschau-Haus Frankfurter Rundschau ialah surat kabar harian Jerman, bermarkas di Frankfurt am Main. Pertama kali terbit pada 1 Agustus 1945, sebagai surat kabar pertama di Jerman yang diduduki AS dan kedua di Jerman pascaperang. Kini dimiliki oleh Druck und Verlagshaus Frankfurt am Main GmbH dan mencapai oplah 181.000. Rundschau ialah harian kedua Jerman yang dicetak setelah PD II, dan harian pertama di sektor Amerika. Hans Habe, seorang war...

Hak lesbian, gay, biseksual, transgender (LGBT) di Eropa bervariasi menurut negara. Lima dari tujuh negara yang telah melegalisir pernikahan sesama jenis terletak di Eropa. Meskipun pernah terjadi penganiayaan terhadap kaum lesbian dan gay dari masa Kekaisaran Romawi hingga abad ke-20, kaum gay lebih diterima di Eropa dibanding di benua lainnya. Legislasi menurut negara Artikel utama: Hak LGBT menurut negara Eropa Utara Negara Homoseksual legal? Pengakuan hubungan sesama jenis Pernikahan sesa...

Pour les articles homonymes, voir Frein (homonymie). Un frein est un système permettant de ralentir, voire d'immobiliser, les pièces d'une machine ou d'un véhicule. Dans le cas de mouvements, la plupart des types de freins transforment l’énergie cinétique en énergie thermique par friction de pièces mobiles sur des pièces fixes, éléments qu'il faut refroidir. D'autres systèmes convertissent l’énergie cinétique en une autre forme d'énergie (par exemple électrique ou pneumati...
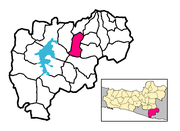
SidoharjoKecamatanPeta lokasi Kecamatan SidoharjoNegara IndonesiaProvinsiJawa TengahKabupatenWonogiriPemerintahan • Camat-Populasi • Total38,260 (2.003) jiwaKode Kemendagri33.12.14 Kode BPS3312160 Luas57,20 km²Desa/kelurahan- Sidoharjo (Jawa: ꦱꦶꦢꦺꦴꦲꦂꦗꦺꦴ) adalah sebuah kecamatan di Kabupaten Wonogiri, provinsi Jawa Tengah, Indonesia. Batas wilayah Batas-batas wilayahnya adalah sebagai berikut: Utara Kecamatan Girimarto Timur kecamatan Jatis...

Timunan Leptochloa chinensis TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmonocotsKladcommelinidsOrdoPoalesFamiliPoaceaeSubfamiliChloridoideaeTribusChlorideaeSubtribusEleusininaeGenusLeptochloaSpesiesLeptochloa chinensis Nees, 1824 Tata namaBasionimPoa chinensis lbs Leptochloa chinensis, umumnya dikenal sebagai rumput timunan, adalah spesies rumput dalam keluarga Poaceae . Ini adalah gulma padi yang serius. [1] Ini dikenal sebagai rumput padang rumput dan meru...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

City in California, United States For other uses, see Santee (disambiguation). City in California, United StatesSantee, CaliforniaCity FlagSealMotto(s): Do More, Due East; East County’s Best Kept Secret;[1] Sustainable Santee[2]Location within San Diego CountySanteeLocation within San Diego CountyShow map of San Diego County, CaliforniaSanteeLocation within CaliforniaShow map of CaliforniaSanteeLocation within the United StatesShow map of the United StatesCoordinates: 3...

Armenian television singing competition This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Voice of Armenia – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) The Voice of ArmeniaArmenianՀայաստանի ձայնըHayastani Dzayne GenreReality competitionCreated byJohn de MolJudges Nune Yesayan (2...

Series of vampire romance novels by Stephenie Meyer TwilightThe six covers for the Twilight novel series. Twilight (2005) New Moon (2006) Eclipse (2007) Breaking Dawn (2008) Life and Death: Twilight Reimagined (2015) Midnight Sun (2020) AuthorStephenie MeyerCountryUnited StatesLanguageEnglishGenreFantasy romance, young adult fictionPublisherLittle, Brown and CompanyPublished2005–2020Media typePrintNo. of books5 (with 3 companions) Twilight is a series of four fantasy romance novels, two com...

American gymnastics coach (born 1968) Corrinne TarverAlternative name(s)Corrinne WrightBorn1968 (age 55–56)HometownMount Vernon, New York, U.S.Height4 ft 9 in (145 cm)[a]Years on national team1985–1986 (U.S.)College teamGeorgia (1987–1990)Former coach(es)Suzanne Yoculan (Georgia) Medal record Representing Georgia GymDogs NCAA Championships 1987 Salt Lake City Team 1989 Athens Team 1989 Athens All Around 1989 Athens Floor 1987 Salt Lake City Floor 198...

明朝关西八卫 赤斤蒙古卫,明朝关西八卫之一,简称赤斤卫,又作赤金卫。 明朝 明朝永乐二年(1404年)元朝丞相苦术之子塔力尼投降明朝,以其所部在赤斤站设置赤斤蒙古千户所,在今甘肃省玉门市西北赤金堡。永乐八年(1410年)升为赤斤卫,正德年间被吐鲁番汗国所破,当地人内徙肃州的南山,赤斤城空。 清朝 清圣祖康熙五十七年(1718年),恢复赤金卫,清世宗雍正...

Proto-Indo-Iranian sound law This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) An editor has performed a search and found that sufficient sources exist to establish the subject's notability. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bartholomae's law – news · newspapers ...

Leonardo da Vinci's Mona Lisa is an Italian art masterpiece worldwide famous. Since ancient times, Greeks, Etruscans and Celts have inhabited the south, centre and north of the Italian peninsula respectively. The very numerous rock drawings in Valcamonica are as old as 8,000 BC, and there are rich remains of Etruscan art from thousands of tombs, as well as rich remains from the Greek colonies at Paestum, Agrigento and elsewhere. Ancient Rome finally emerged as the dominant Italian and Europe...

2009 2019 Élections européennes de 2014 en Lettonie 8 députés européens pour la Lettonie 24 mai 2014 Corps électoral et résultats Inscrits 1 472 478 Votants 445 225 30,24 % Votes exprimés 440 288 Votes blancs 4 937 Unité – Valdis Dombrovskis Voix 204 979 46,19 % Sièges obtenus 4 Alliance nationale – Roberts Zīle Voix 63 229 14,25 % Sièges obtenus 1 Parti social-démocrate « Ha...

Darker than Black character Fictional character HeiDarker than Black characterPromotional illustration of HeiFirst appearanceDarker than Black episode 1: The Fallen Star of a Contract (Part 1) (April 5, 2007)Created byTensai OkamuraDesigned byYuji IwaharaVoiced byHidenobu Kiuchi (Japanese)Jason Liebrecht (English)In-universe informationAliasLi Shenshun, BK-201GenderMaleRelativesBai (sister) Hei (Japanese: 黒(ヘイ), pinyin: Hēi, lit. Black), also known as Li Shenshun (李舜生(�...

Railway station in Kerala, India This article is about the railway station. For the town, see Mayyanad. For the city, see Kollam. MayyanadExpress train & Passenger train stationMayyanad railway stationGeneral informationLocationMukkom Road, Mayyanad, Kollam, KeralaIndiaCoordinates8°50′17″N 76°38′52″E / 8.8381°N 76.6478°E / 8.8381; 76.6478Owned byIndian RailwaysOperated bySouthern Railway zoneLine(s)Kollam–Thiruvananthapuram trunk linePlatforms2Tracks2...

この記事の主題はウィキペディアにおける組織の特筆性の基準を満たしていないおそれがあります。 基準に適合することを証明するために、記事の主題についての信頼できる二次資料を求めています。なお、適合することが証明できない場合には、記事は統合されるか、リダイレクトに置き換えられるか、さもなくば削除される可能性があります。出典検索?: 日本�...






























![{\displaystyle \left\|{a}\right\|={\sqrt[{}]{(a\cdot {}a)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74fef506fce519d7bbf1a8b64f758cc459c990de)