Circuncentro de masas
|
Read other articles:

Der Regimentsinhaber, Feldmarschall Sachsen-Coburg-Saalfeld Dragoner 1762 Das Regiment war ein Kavallerieverband, der 1683 als Herbeville-Dragoner für die kaiserlich-habsburgische Armee errichtet wurde. Das Regiment wechselte mehrfach den Namen und hieß zuletzt „k.k. Dragonerregiment „Feldmarschall Friedrich Josias Prinz zu Sachsen – Coburg – Saalfeld“ Nr. 6“ In der 1769 erstellten Kavallerie-Rangliste wurde dem Regiment die Bezeichnung Cavallerie-Regiment Nr. 37 zugewiesen, 179...

Tentara Kekaisaran RusiaРусская императорская армияLambang Tentara Kekaisaran RusiaAktif1721–1917Negara Kekaisaran RusiaTipe unitTentaraJumlah personel12 – 15.000.000 selama Perang Dunia I4.200.000 selama Perang Saudara RusiaMaskotPertempuranPerang Utara RayaSejarah Pertempuran Rusia-TurkiDaftar Pertempuran Rusia dan SwediaPertempuran Rusia-PersiaDaftar konflik bersenjata yang melibatkan Polandia melawan RusiaPerang Tujuh TahunPeperangan era NapoleonPerang Ka...

PBN beralih ke halaman ini. Untuk kegunaan lain, lihat PBN (disambiguasi). Partai Barisan Nasional SingkatanBarnasDibentuk1 Oktober 2007Kantor pusatJalan Gunawarman No. 32, Kebayoran Baru, JakartaIdeologiPancasilaKursi di DPRTidak adaSitus webSitus web resmiPolitik IndonesiaPartai politikPemilihan umum Partai Barisan Nasional, biasanya disebut Partai Barnas, adalah sebuah partai politik di Indonesia. Partai ini didirikan pada tanggal 1 Oktober 2007 di Jakarta oleh Ventje Rumangkang, salah sat...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Siklon tropis – berita · surat kabar · buku · cendekiawan · JSTOR Dalam meteorologi, siklon tropis (atau angin topan, angin puyuh, badai tropis, taifun, atau angin ribut tergantung pada daerah dan kekuatannya...

Questa voce sull'argomento calciatori argentini è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Alan Ruiz Ruiz in azione con lo Sporting Lisbona nel 2016 Nazionalità Argentina Altezza 183 cm Peso 78 kg Calcio Ruolo Centrocampista Squadra Sport Recife Carriera Giovanili 1998-2011 Gimnasia (LP) Squadre di club1 2011-2012 Gimnasia (LP)29 (0)2012-2013 San Lorenzo34 (3)2014→ &#...
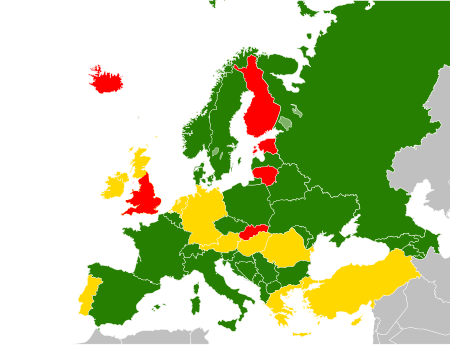
Minimum age at which a person can legally purchase or consume alcoholic beverages This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Legal drinking age – news · newspapers ...

American-bred Thoroughbred racehorse This article is about the American Thoroughbred racehorse. For the voting process, see Early voting. Early VotingEarly Voting at Preakness StakesSireGun RunnerGrandsireCandy Ride (ARG)DamAmour D'EteDamsireTiznowSexColtFoaledMarch 7, 2019[1]CountryUnited StatesColourBayBreederThree Chimneys FarmOwnerKlaravich StablesTrainerChad C. BrownRecord6: 3-1-0Earnings$1,372,500[2]Major winsWithers Stakes (2022)American Triple Crown wins:Preakness Stak...

33rd season of second-tier NASCAR Nationwide Series 2014 NASCAR Nationwide Series Previous 2013 Next 2015 Champions | Seasons Chase Elliott, the 2014 Nationwide Series champion & 2014 Nationwide Series Rookie of the Year. Regan Smith finished second behind his teammate Elliott in the championship by 42 points. Elliott Sadler finished third in the championship, 59 points behind Elliott. The No. 22 car for Team Penske won the owner's championship with 1347 points and five differen...

Genus of mammals Howler monkeys[1] Brown howler monkey Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Atelidae Subfamily: AlouattinaeTrouessart, 1897 (1825) Genus: AlouattaLacépède, 1799 Type species Simia belzebulLinnaeus, 1766 Species See text Alouatta distribution Synonyms Mycetes Illiger, 1811 Stentor É. Geoffroy, 1812 Howler monkeys (genus Alouatta, monotypic in...

أبو المعالي عبد العزيز بن الحسين السعدي معلومات شخصية الميلاد 490 هـ1097 مصقلية الوفاة 561 هـ 1166 مالقاهرة، مصر مواطنة الدولة الفاطمية الحياة العملية الفترة العصر العباسي النوع أدب عربي تقليدي الحركة الأدبية الأدب في العصر العباسي الثاني (تجزؤ الخلافة) المهنة شاعر اللغات ا�...

Nepali politician Jeevan Ram Shresthaजीवन राम श्रेष्ठMinister of Culture, Tourism and Civil AviationIn office27 June 2022 – 26 December 2022PresidentBidhya Devi BhandariPrime MinisterSher Bahadur DeubaPreceded byPrem AleSucceeded bySudan KiratiMember of Parliament, Pratinidhi SabhaIn office4 March 2018 – 18 September 2022Preceded byNabindra Raj JoshiSucceeded byBiraj Bhakta ShresthaConstituencyKathmandu 8Chair of Nepal Olympic CommitteeIncumbe...

РХМ «Кашалот» РХМ «Кашалот» — радянська розвідувальна хімічна машина. Створена на базі багатоцільового легкоброньованого тягача МТ-ЛБ. Зміст 1 Опис 2 Оператори 3 Література 4 Примітки Опис РХМ «Кашалот» призначена для радіаційної, хімічної та, частково, бактеріологіч�...

This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (September 2016) (Learn how and when to remove this message) Economy of HaryanaGurgaon, the city's DLF Cyber City that houses some of the top IT & Fortune 500 companies.CurrencyIndian Rupee (INR, ₹)Fiscal year1 April – 31 MarchCountry group Developing/Emerging[1] Upper-middle income eco...

Staatstramwegen op CelebesIkhtisarKantor pusat Makassar, Hindia BelandaLokalSulawesi SelatanTanggal beroperasi1922–1930Penerus Keisei Railway[1] Direktorat Jenderal Perkeretaapian (regulator) Kereta Api Indonesia (operator sarana) Celebes Railway Indonesia (operator prasarana) TeknisLebar sepur1.067 mm (3 ft 6 in)Panjang jalur47 km Staatstramwegen op Celebes (STC) adalah divisi dari Staatsspoorwegen yang membangun dan mengoperasikan jalur kereta api Pasarbutu...

Bilateral relationsCanadian–Israeli relations Canada Israel Diplomatic missionEmbassy of Canada, Tel AvivEmbassy of Israel, Ottawa Canada and Israel share bilateral diplomatic, commercial, and cultural ties. Canada recognised Israel on 11 May 1949, three days before the first anniversary of the Israeli Declaration of Independence, and currently maintains an embassy in Tel Aviv;[1] Israel maintains an embassy in Ottawa and regional[clarification needed] consulates in Montreal...

American chemist and professor For his father, a chemist of the same name, see Benjamin Silliman. Benjamin Silliman Jr.Benjamin Silliman Jr. c. 1865Born(1816-12-04)December 4, 1816New Haven, ConnecticutDiedJanuary 14, 1885 (1885-01-15) (aged 68)New Haven, ConnecticutAlma materYale UniversityKnown foroilScientific careerFieldschemistry Signature Benjamin Silliman Jr. (December 4, 1816 – January 14, 1885) was a professor of chemistry at Yale University and instrumental in ...

Conversion of molecular nitrogen into biologically accessible nitrogen compounds Nitrogen fixation is a chemical process by which molecular dinitrogen (N2) is converted into ammonia (NH3).[1] It occurs both biologically and abiologically in chemical industries. Biological nitrogen fixation or diazotrophy is catalyzed by enzymes called nitrogenases.[2] These enzyme complexes are encoded by the Nif genes (or Nif homologs) and contain iron, often with a second metal (usually moly...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW • CAPES • Google (N • L • A)). (Fevereiro de 2019) Luís XII Luís XII de França Rei da França Reinado 7 de abril de 1498a 1 de janeiro de 1515 Coroação 27 de maio de 1498 Antecessor(a) Carlos VIII Sucessor(a) Francisco I Nascimento 27 de junho de 1462 Castelo de Blois, Loir-et-Cher, França Morte 1...

Chữ Kirin ZhweHệ chữ KirinMẫu tự SlavАБВГҐДЂЃЕЀЁЄЖЗЗ́ЅИЍІЇЙЈКЛЉМНЊОПРСС́ТЋЌУЎҮФХЦЧЏШЩЪЫЬЭЮЯMẫu tự ngôn ngữ phi SlavӐА̄А̊А̃ӒӒ̄ӘӘ́Ә̃ӚӔҒГ̧Г̑Г̄ҔӺӶԀԂꚂꚀꚈԪԬӖЕ̄Е̃Ё̄Є̈ӁҖꚄӜԄҘӞԐԐ̈ӠԆӢИ̃ҊӤҚӃҠҞҜԞԚӅԮԒԠԈԔӍӉҢԨӇҤԢԊО̆О̃О̄ӦӨӨ̄ӪҨԤҦР̌ҎԖҪԌꚐҬꚊꚌԎУ̃ӮӰӰ́ӲҮҮ́ҰХ̑ҲӼӾҺҺ̈ԦꚔҴꚎҶӴӋҸꚒꚖꚆҼҾЫ̆Ы̄ӸҌЭ̆Э̄Э�...

Sân bay NarimanovoАэропорт Нариманово IATA: ASF - ICAO: URWA Tóm tắt Kiểu sân bayPublicCơ quan điều hànhJSC Aeroport AstrakhanPhục vụAstrakhan Độ cao AMSL -65 ft (-20 m) Tọa độ 46°17′0″B 48°00′22,6″Đ / 46,28333°B 48°Đ / 46.28333; 48.00000 Đường băng Hướng Chiều dài Bề mặt ft m 09/27 8.202 2.500 bê tông Sân bay Narimanovo (tiếng Nga: Аэропорт Нариманово) (IATA: ASF, ICAO: URWA...











