Cicadidae
| ||||||||||||||||||||||||||||||||||
Read other articles:

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Lukisan potret Urashima Tarō oleh Utagawa Kuniyoshi Urashima Tarō (浦島太郎code: ja is deprecated ) adalah legenda Jepang tentang seorang nelayan bernama Urashima Tarō. Ia diundang ke Istana Laut (Istana Ryūgū) setelah menyelamatkan seekor penyu. Dalam catatan sejarah Provinsi Tango (Tango no kuni fudoki) terdapat cerita berjudul Urashima no ko (浦嶼子code: ja is deprecated )[1][pranala nonaktif permanen], tetapi menceritakan tentang delapan bidadari yang turun dari langit...

Irish revolutionary and republican politician (1874–1922) Cathal BrughaMinister for DefenceIn office1 April 1919 – 9 January 1922PresidentÉamon de ValeraPreceded byRichard MulcahySucceeded byRichard MulcahyCeann Comhairle of Dáil ÉireannIn office21 January 1919 – 22 January 1919DeputyJohn J. O'KellyPreceded byOffice establishedSucceeded byCount PlunkettPresident of Dáil ÉireannIn office21 January 1919 – 1 April 1919Preceded byNew officeSucceeded byÉamo...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

ميت النور - قرية مصرية - تقسيم إداري البلد مصر المحافظة الغربية المركز زفتى وحدة محلية سنباط المسؤولون السكان التعداد السكاني 3,802 نسمة (إحصاء 2006) معلومات أخرى التوقيت ت ع م+02:00 تعديل مصدري - تعديل ميت النور إحدى قرى مركز زفتى التابع لمحافظة الغربية بجمه...

الدوري الوطني 2002–03 تفاصيل الموسم دوري الدرجة الخامسة الإنجليزي [لغات أخرى] النسخة 24 البلد المملكة المتحدة البطل يوفل تاون الدوري الوطني 2001–02 الدوري الوطني 2003–04 تعديل مصدري - تعديل الدوري الوطني 2002–03 هو موسم من الدوري الوطني [لغات أ...

فيلم درجة ثانيةروجر كورمان «ملك أفلام الدرجة الثانية», أنتج وأخرج فيلم العقاب (1963) لصالح شركة أميريكان إنترناشنال. تصدر فينسنت برايس الدور مع ممثلين قدماء بالإضافة إلى جاك نيكلسون الشاب.صنف فرعي من فيلم منخفض التكلفة فروع الغرب الأمريكي — فيلم خيال علمي — فيلم رعب تعديل - �...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...
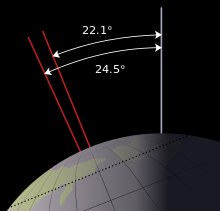
Global climate cycles Past and future Milankovitch cycles via VSOP modelGraphic shows variations in five orbital elements: Axial tilt or obliquity (ε). Eccentricity (e). Longitude of perihelion (sin(ϖ)). Precession index (e sin(ϖ))Precession index and obliquity control insolation at each latitude: Daily-average insolation at top of atmosphere on summer solstice ( Q ¯ d a y {\textstyle {\overline {Q}}^{\mathrm {day} }} ...

Rivalry between football clubs Chelsea F.C. v Tottenham Hotspur F.C.Chelsea and Tottenham Hotspur contesting the 2015 Football League Cup final.LocationLondonTeams Chelsea Tottenham Hotspur First meeting18 December 1909First DivisionChelsea 2–1 Tottenham HotspurLatest meeting2 May 2024Premier LeagueChelsea 2–0 Tottenham HotspurStadiumsStamford Bridge (Chelsea)Tottenham Hotspur Stadium (Spurs)StatisticsMeetings total177Most winsChelsea (79)Top scorerJimmy Floyd Hasselbaink (12)[1]A...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Yoru o Yuke – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this message) 1990 studio album by Miyuki NakajimaYoru o YukeStudio album by Miyuki NakajimaReleasedJune 13, 1990RecordedBurnish Stone, Epicurus, Music Inn, Sound Vall...

DuplicateFilm posterSutradaraMahesh BhattProduserYash JoharDitulis olehRobin BhattAkash KhuranaJaved SiddiqiPemeranShahrukh KhanJuhi ChawlaSonali BendreFarida JalalPenata musikAnu MalikSinematograferSameer AryaPenyuntingWaman BhonsleDistributorDharma ProductionsTanggal rilis 8 Mei 1998 (1998-05-08) Durasi166 menitNegaraIndiaBahasaHindiAnggaran₹9,5 crore (setara dengan ₹305 crore atau US$43 juta pada tahun 2023)[1]Pendapatankotor₹21,49 crore (setara d...

Artikel ini bukan mengenai Matematika. Untuk kegunaan lain, lihat Mathematica (disambiguasi). Mathematica Tampilan Mathematica 8.0.0 LinuxTipebahasa pemrograman, computer algebra system (en) , mathematical software (en) , array programming language (en) , bahasa pemrograman fungsional, data analysis software (en) , visualization software (en) dan bahasa pemrograman diinterpretasi Versi pertama23 Juni 1988[1]Versi stabilDaftar 1.0 (23 Juni 1988) 1.1 (31 Oktober 1988) 1.2 (1r Agustus 19...

This article is missing information about bacteria/organelle, archaea (rDNA operons — the euk ones are technically polycistronic too); canonical inclusion of 5S in these groups; plastid 4.5S; occurrence of nonclassical unlinked variants (PMID 31712737). Please expand the article to include this information. Further details may exist on the talk page. (October 2021) The ribosomal DNA (abbreviated rDNA) consists of a group of ribosomal RNA encoding genes and related regulatory elements, ...

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 H He 2 Li Be B C N O F Ne 3 Na Mg Al Si P S Cl Ar 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 5 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 6 Cs Ba * Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 7 Fr Ra ** Rf Db Sg Bh Hs Mt Ds Rg Cn Nh Fl Mc Lv Ts Og 8 Uue Ubn ⁂ Uth Uts Uto Ute Uqn Uqu Uqb ↓ * La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm

Chinese general and politician (1916–2015) In this Chinese name, the family name is Wang. Wang Dongxing汪东兴Wang Dongxing in 1955, as chief of Mao's personal security forceVice Chairman of the Chinese Communist PartyIn officeAugust 1977 – February 1980ChairmanHua Guofeng Personal detailsBorn(1916-01-09)9 January 1916Yiyang County, Jiangxi, ChinaDied21 August 2015(2015-08-21) (aged 99)Beijing, ChinaPolitical partyChinese Communist Party Wang Dongxing (Chinese: 汪东�...

British historian (born 1940) For other people with the same name, see John Dunn (disambiguation). This biography of a living person includes a list of general references, but it lacks sufficient corresponding inline citations. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately, especially if potentially libelous or harmful. Please help to improve this article by introducing more precise citations. (October 2016) (Learn how and when to re...

Village in Pljevlja, MontenegroVidreVillageVidreLocation within MontenegroCoordinates: 43°20′55″N 19°17′55″E / 43.3486°N 19.2986°E / 43.3486; 19.2986Country MontenegroMunicipality PljevljaPopulation (2011) • Total182Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Vidre (Serbian Cyrillic: Видре) is a village in the municipality of Pljevlja, Montenegro. Demographics According to the 2003 census, the village had a populat...

Submarine-launched ballistic missile UGM-96 Trident I (C4) The first launch of a Trident I with a drag-reducing aerospike, from Cape Canaveral, on 18 January 1977TypeSLBMPlace of originUnited StatesService historyIn service1979 to 2005Used byUnited States NavyProduction historyManufacturerLockheed Missiles DivisionSpecificationsMass73,066 pounds (33,142 kg)Length33 feet (10.2 m)Diameter71 inches (1.8 m)WarheadUp to eight W76 warheads in Mark 4 RBs with a yie...

Relative distance of a point from a circle Geometric meaning In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.[1] Specifically, the power Π ( P ) {\displaystyle \Pi (P)} of a point P {\displaystyle P} with respect to a circle c {\displaystyle c} with center O {\displaystyle O} and radius r {\displaystyle r} is defined by Π ( P ) = | P O ...







