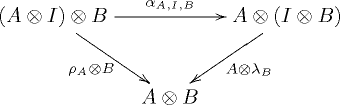
Categoría monoidal
|
Read other articles:

Invasi Mongol ke KoreaTanggal1231-1273LokasiSemenanjung KoreaHasil Kapitulasi Dinasti GoryeoPihak terlibat Dinasti Goryeo Korea Kekaisaran MongolTokoh dan pemimpin Choe UPark SeoKim Yun-huBae JungsonKim Tong-jeong Ögedei KhanMongke KhanSalietaiJalairtai Bagian dari seri mengenai Sejarah Korea Prasejarah Zaman Jeulmun Zaman Mumun Kuno Gojoseon 2333 SM - 108 SM Jin Proto Tiga Kerajaan Buyeo Goguryeo Okjeo Dongye Samhan Mahan Byeon Jin Empat Jun di Dinasti Han Tiga Kerajaan Goguryeo 37 SM – 6...

Bukit She Bukit She, Observatorium Sheshan (kiri) dan Basilika Sheshan (tengah) Hanzi: 佘山 Makna harfiah: Bukit She (nama marga) Alih aksara Mandarin - Hanyu Pinyin: Shéshān - Wade-Giles: She Shan Wu - Romanisasi: Zosai Bukit She (佘山, Shéshān) atau dalam dialek Shanghai disebut Zosai, adalah sepasang bukit di Distrik Songjiang, Shanghai, Tiongkok. Sepasang bukit ini terdiri dari Bukit Barat (97,2 mdpl) dan Bukit Timur (72,4 mdpl).[1] Karena Bukit Barat dianggap lebih penti...

Ornamen ukiran teratai (Kambang Talipuk) pada dinding depan Rumah Bubungan Tinggi Anjungan Kalimantan Selatan TMII Jakarta. Ornamen ukiran teratai (Kambang Talipuk) pada Rumah Bubungan Tinggi Desa Habirau, HSS, Kalimantan Selatan Kambang Talipuk (artinya bunga teratai) adalah salah satu motif ukiran khas etnik Banjar dalam bentuk tatah surut (relief) dalam wujud sulur-suluran bunga teratai (Kambang Talipuk) yang diterapkan pada Rumah Bubungan Tinggi (Rumah Banjar). Motif kambang talipuk di uk...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2024. Moulins - Montbeugny AirportAéroport de Moulins - MontbeugnyIATA: XMUICAO: LFHYInformasiJenisPublicPengelolaCCI de Moulins et VichyMelayaniMoulins, Allier, FranceKetinggian dpl279 mdplLandasan pacu Arah Panjang Permukaan m kaki 08/26 1,300 4,2...

Kris Kobach Sekretaris Negara Bagian Kansas ke-31Masa jabatan10 Januari 2011 – 14 Januari 2019GubernurSam BrownbackJeff Colyer PendahuluChris BiggsPenggantiScott SchwabKetua Partai Republik KansasMasa jabatan28 Januari 2007 – 31 Januari 2009 PendahuluTim ShallenburgerPenggantiAmanda Adkins Informasi pribadiLahirKris William Kobach26 Maret 1966 (umur 58)Madison, Wisconsin, Amerika SerikatPartai politikRepublikSuami/istriHeather Mannschreck (m. 202...

Ursula FranklinCC OOnt FRSCFranklin di peluncuran The Ursula Franklin Reader pada tahun 2006LahirUrsula Maria Martius(1921-09-16)16 September 1921München, JermanMeninggal22 Juli 2016(2016-07-22) (umur 94) Toronto, Ontario, KanadaKebangsaanJerman-KanadaWarga negaraKanadaAlmamaterUniversitas Teknik BerlinUniversitas TorontoDikenal atasArkeometriPasifismeFeminismeTeori teknologiSuami/istriFred Franklin (m. 1952)PenghargaanGovernor General's Award (19...

Citroën CX1983 Citroën CX PrestigeInformasiProdusenCitroënMasa produksi1974–1991PerakitanAulnay-sous-Bois, Prancis[1]Arica, ChiliVigo, SpanyolPerancangRobert Opron Geoff Matthews (Series 2 refresh)Bodi & rangkaKelasmobil mewah ukuran medium / Mobil eksekutif (E)Bentuk kerangka4-pintu fastback4-pintu fastback long wheelbase5-pintu brake (estate)Tata letakmesin depan, penggerak roda depanPenyalur dayaMesin2.0L I42.2L I42.3L I42.4L I42.5L Diesel I4Transmisi5-percepatan manu...

Paul RuddPaul Rudd di acara penayangan perdana Ant-Man bulan Juni 2015LahirPaul Stephen Rudd6 April 1969 (umur 55)Passaic, New Jersey, A.S.AlmamaterUniversitas KansasAmerican Academy of Dramatic ArtsPekerjaanAktorproduserpenulis skenarioTahun aktif1991–sekarangKaryaDaftar lengkapSuami/istriJulie Yaeger (m. 2003)Anak2PenghargaanDaftar lengkap Paul Stephen Rudd (lahir 6 April 1969) adalah aktor Amerika. Dia belajar teater di Universitas Kansas dan Ame...

Artikel ini bukan mengenai Wittenberg. Wittenberge BenderaLambang kebesaranLetak Wittenberge di Prignitz Wittenberge Tampilkan peta JermanWittenberge Tampilkan peta BrandenburgKoordinat: 53°00′N 11°45′E / 53.000°N 11.750°E / 53.000; 11.750Koordinat: 53°00′N 11°45′E / 53.000°N 11.750°E / 53.000; 11.750NegaraJermanNegara bagianBrandenburgKreisPrignitz Subdivisions7 Stadtteile/StadtbezirkePemerintahan • MayorOliver Herma...

Indian Navy special operations force This article is about The Indian Navy special forces. For other uses, see Marcos. Not to be confused with MARSOC. MARCOSMARCOS PatchActiveFebruary 1987 – present(37 years, 2 months)[1]Country IndiaBranch Indian NavyTypeSpecial Operations ForcesSizeClassifiedHeadquartersINS Karna, Vishakapatnam, IndiaNickname(s)Magarmach (The Crocodiles),[2]Dadhiwala Fauj (The bearded army)[3][4]Motto(s)The Few, The...

Cinema of Bangladesh List of Bangladeshi films 1928–1947 India 1948–1958 East Pakistan 1959–1970 East Pakistan 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971–1979 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000s 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010s 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020s 2020 2021 2022 2023 vte The Dhal...

2012 album by Keane StrangelandStudio album by KeaneReleased4 May 2012Recorded2011–12StudioSea Fog Studios (East Sussex, England)RAK Studios (London, England)Air Lyndhurst Hall (London, England)GenreAlternative rock, indie popLength45:08LabelIslandProducerDan Grech-MargueratKeane chronology Night Train(2010) Strangeland(2012) The Best of Keane(2013) Singles from Strangeland Silenced by the NightReleased: 13 March 2012 DisconnectedReleased: 27 April 2012 Sovereign Light CaféReleased: 23...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Nathanael Greene – berita · surat kabar · buku · cendekiawan · JSTORArtikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tida...

Pour les articles homonymes, voir Taras Chevtchenko (homonymie) et Chevtchenko. Taras ChevtchenkoТарас Шевченко Autoportrait de Taras Chevtchenko en 1840. Données clés Nom de naissance Taras Hryhorovytch Chevtchenko Alias le kobzar Naissance 9 mars 1814 Moryntsi, Gouvernement de Kiev, Empire russe Décès 10 mars 1861 (à 47 ans) Saint-Pétersbourg, Empire russe Activité principale poète, peintre Formation Académie russe des Beaux-Arts Auteur Langue d’écriture ukrai...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Railway station in the East Riding of Yorkshire, England BridlingtonGeneral informationLocationBridlington, East Riding of YorkshireEnglandCoordinates54°05′02″N 0°11′55″W / 54.0840°N 0.1985°W / 54.0840; -0.1985Grid referenceTA178668Managed byNorthernPlatforms3 (numbered 4-6)Other informationStation codeBDTClassificationDfT category DHistoryOriginal companyYork and North Midland RailwayPre-groupingNorth Eastern RailwayPost-groupingLondon and North Eastern Ra...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (juillet 2018). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Cet article traite uniquement de la compétition masculine. Pour la compétition féminine, voir...

Mary Lynn Rajskub Mary Lynn Rajskub (lahir 22 Juni 1971) merupakan seorang aktris berkebangsaan Amerika Serikat yang memiliki keturunan Ceko dan Irlandia. Bermain di film utamanya seperti Mysterious Skin, Legally Blonde 2, Sweet Home Alabama, Dude, Where's My Car?, Man on the Moon, Punch-Drunk Love, The Anniversary Party, Firewall, dan Little Miss Sunshine. Dia dilahirkan di Trenton, Michigan. Dia berkarier di dunia film sejak tahun 1999. Filmografi Tahun Judul Peran Keterangan 1997 Who's the...