Cálculo umbral
|
Read other articles:

Jungle ShuttlePoster filmSutradara Taedong Park Mauricio De la Orta Produser Yongjin Kwon Executive: Mark A.Z. Dippé Ditulis oleh Mauricio De la Orta Johnny Hartmann Jean Dubois Morfin Jean Dubois Renaud Brad Schreiber Zach Strauss Cerita Jean Dubois Renaud Duane Orville Trejo Pemeran Drake Bell Rob Schneider Alicia Silverstone Tom Arnold Penata musikMario SantosPenyunting Alex Agoston Youngwan Ko Perusahaanproduksi Animation Picture Company Avikoo Studios Emotion Collective Design Wes...

Peta menunjukkan lokasi Omar Omar adalah munisipalitas yang terletak di provinsi Sulu, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 25.102 jiwa dan 3.586 rumah tangga. Pembagian wilayah Secara administratif Omar terbagi menjadi 8 barangay, yaitu: Andalan Angilan Capual Island Huwit-huwit Lahing-Lahing Niangkaan Sucuban Tangkuan Pranala luar Basilan, Sulu Have 5 New Towns Memorandum Order No. 260 Diarsipkan 2010-04-11 di Wayback Machine. Philippine Standard Geographic...

1984 Élections européennes de 1979 en France 10 juin 1979 Postes à élire 81 sièges au Parlement européen Corps électoral et résultats Votants 21 356 960 60,71 % Votes exprimés 20 242 347 Votes blancs 1 114 613 UDF – Simone Veil Voix 5 588 851 27,61 % Sièges obtenus 25 PS-MRG – François Mitterrand Voix 4 763 026 23,53 % Sièges obtenus 22 PCF – Georges Marchais V...

العلاقات الكيريباتية الناوروية كيريباتي ناورو كيريباتي ناورو تعديل مصدري - تعديل العلاقات الكيريباتية الناوروية هي العلاقات الثنائية التي تجمع بين كيريباتي وناورو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ا...

Country and WestAlbum studio karya Dottie WestDirilisMei 1970Direkam1970 at RCA Victor Studio, Nashville, TNGenreCountry, Nashville SoundLabelRCAProduserDanny DavisKronologi Dottie West Makin' Memories (1969)Makin' Memories1969 Country and West (1970) Forever Yours (1970)Forever Yours1970 Country and West adalah album musik country penyanyi, Dottie West. Album ini dirilis pada tahun 1970. Daftar lagu It's Dawned on Me You're Gone (Hank Cochran, Red Lane) As Long As I Love (Dolly Parton) L...

4th episode of the 5th season of The Simpsons RosebudThe Simpsons episodePromotional image for the episode, depicting Homer with the RamonesEpisode no.Season 5Episode 4Directed byWes ArcherWritten byJohn SwartzwelderProduction code1F01Original air dateOctober 21, 1993 (1993-10-21)Guest appearance The Ramones as themselves Episode featuresCouch gagThe family finds identical copies of themselves sitting on the couch.[1]CommentaryMatt GroeningDavid MirkinWes ArcherDa...

العلاقات البوروندية التوغولية بوروندي توغو بوروندي توغو تعديل مصدري - تعديل العلاقات البوروندية التوغولية هي العلاقات الثنائية التي تجمع بين بوروندي وتوغو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة �...

Dancing with a StrangerSingel oleh Sam Smith dan Normanidari album Love GoesDirilis11 Januari 2019Direkam2018StudioThe Stellar House; Venice, California[1]Genre Disko R&B pop Durasi2:51LabelCapitolPencipta Sam Smith Jimmy Napes Mikkel S. Eriksen Tor E. Hermansen Normani Kordei Hamilton Produser Stargate Jimmy Napes Kronologi singel Sam Smith Fire on Fire (2018) Dancing with a Stranger (2019) How Do You Sleep? (2019) Kronologi singel Normani Waves(2018) Dancing with a Str...
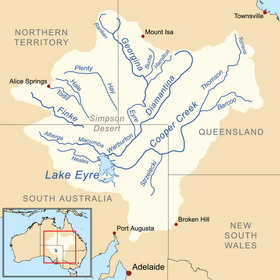
Kati Thanda–Lake EyreGambar satelit komposit Landsat 7 dengan panjang gelombang inframerah gelombang pendek, inframerah dekat, dan biruPeta cekungan Danau Eyre, dengan danau di bawah kiriLetakBagian utara Australia SelatanKoordinat28°22′S 137°22′E / 28.367°S 137.367°E / -28.367; 137.367Koordinat: 28°22′S 137°22′E / 28.367°S 137.367°E / -28.367; 137.367Jenis danauEndoreikAliran masuk utamaSungai WarburtonAliran keluar utamaevapo...
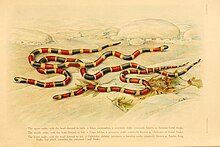
Use of mimicry as an anti-predator adaptation in animals with backbones This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Mimicry in vertebrates – news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this template message) In evolutionary biology, mimicry in vertebrates is mimicry by a vertebrate of some model (an anim...

For the official history of the Song dynasty, see History of Song (book). Part of a series on theHistory of China Timeline Dynasties Historiography Prehistoric Paleolithic Neolithic (c. 8500 – c. 2000 BCE) Yellow, Yangtze, and Liao civilization Ancient Xia (c. 2070 – c. 1600 BCE) Shang (c. 1600 – c. 1046 BCE) Zhou (c. 1046 – c. 256 BCE) Western Zhou (1046–771 BCE) Eastern Zhou (771–256 BCE) Spring and Autumn (c.&...

Overview of the foreign policy of the Recep Tayyip Erdoğan government This article is about the foreign policy of Recep Tayyip Erdoğan while Prime Minister. For his foreign policy as President, see Recep Tayyip Erdoğan § Presidency (2014–present). This article is part of a series aboutRecep Tayyip Erdoğan Early life and career Electoral history Public image Honors Political views Foreign policy 2023 vision Erdoğanism Parties National Salvation Party Welfare Party Virtue Party Jus...

American basketball player, coach and executive Kiki VanDeWegheVanDeWeghe in 2016Personal informationBorn (1958-08-01) August 1, 1958 (age 65)Wiesbaden, West GermanyNationalityAmerican / CanadianListed height6 ft 8 in (2.03 m)Listed weight220 lb (100 kg)Career informationHigh schoolPalisades (Los Angeles, California)CollegeUCLA (1976–1980)NBA draft1980: 1st round, 11th overall pickSelected by the Dallas MavericksPlaying career1980–1993PositionSmall forwardNum...

Domenico PinelliGerejaGereja KatolikKeuskupan agungKeuskupan Agung FermoMasa jabatan1577 - 1584PendahuluFelice Peretti MontaltoPenerusSigismondo ZanettiniImamatTahbisan uskup14 Agustus 1577oleh Paus Gregorius XIIIPelantikan kardinal18 Desember 1585oleh Paus Siktus VPeringkatKardinal-UskupInformasi pribadiLahir(1541-10-21)21 Oktober 1541Genova, ItaliaWafat9 Agustus 1611(1611-08-09) (umur 69)Roma, ItaliaKewarganegaraanItaliaPendidikanSarjana hukumAlmamaterUniversitas Padua Domenico Pi...

Railway station in Ibusuki, Kagoshima Prefecture, Japan This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Miyagahama Station – news · newspapers · books · scholar · JSTOR (January 2012) (Learn how and when to remove this message) Miyagahama Station宮ヶ浜駅General informationLocation4672 Nishikata, Ibusuki, Kagoshima(鹿�...
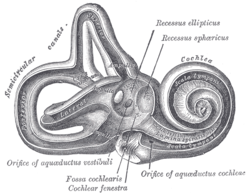
Bony structure of the inner ear Bony labyrinthLateral view of right osseous labyrinthInterior view of right osseous labyrinthDetailsIdentifiersLatinlabyrinthus osseusTA2692FMA60179Anatomical terminology[edit on Wikidata] The bony labyrinth (also osseous labyrinth or otic capsule) is the rigid, bony outer wall of the inner ear in the temporal bone. It consists of three parts: the vestibule, semicircular canals, and cochlea. These are cavities hollowed out of the substance of the bone, and ...

Себежская крепость План крепости в конце XVI века. Реконструкция К. М. Громова 56°16′31″ с. ш. 28°30′13″ в. д.HGЯO Тип Крепость Страна Россия Город Себеж, Псковская область Основатель И. В. Шуйский Первое упоминание 1414 год Дата основания 1535 год Статус Объект культ�...

منتخب الكونغو الديمقراطية لكرة القدم (بالفرنسية: équipe du Zaïre de football) معلومات عامة اللقب Les Léopards (الفهود) بلد الرياضة جمهورية الكونغو الديمقراطية الفئة كرة القدم للرجال رمز الفيفا COD الاتحاد اتحاد جمهورية الكونغو الديمقراطية لكرة القدم كونفدرالية كاف (أفريقيا)...

У этого термина существуют и другие значения, см. Певец (значения). Фрэнк Синатра в студии Певе́ц, певи́ца — тот, кто поёт, занимается пением; исполнитель вокальной музыки: песен, романсов, арий, хоров и т. п.; музыкант, исполняющий музыку на музыкальном инструменте, �...

Indonesian actor In this Indonesian name, there is no family name nor a patronymic. Rd MochtarMochtar in Siti Akbari (1940)Born(1918-05-31)31 May 1918Cianjur, Dutch East IndiesOccupationActorYears active1935–1991Notable work Pareh Terang Boelan Hajji Raden Mochtar (born 31 May 1918), often credited as Rd Mochtar, was an Indonesian actor. Of noble descent, Mochtar was discovered by Albert Balink and first cast in the commercial failure Pareh (1936). Rising to popularity after the releas...






![{\displaystyle \Delta ^{k}[f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fced1443b2629d8ef145f5dda7778d3f73985ff)
}{k!}}(x)_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a9adacadbbe0213c5dfe79e2ed9fed62aab71bc)







