Acuñación de Sylver
|
Read other articles:

U.S. Army Distinguished Service Medal The U.S. Army Distinguished Service Medal Dianugerahkan oleh the Angkatan Darat Amerika Serikat[1] Jenis Medali militer (Penghargaan) Persyaratan penerima Penghargaan dapat diberikan kepada orang selain anggota Angkatan Bersenjata Amerika Serikat hanya untuk layanan masa perang, dan kemudian hanya dalam keadaan luar biasa, dengan persetujuan tertulis dari Presiden dalam setiap kasus.. Dianugerahkan atas dasar Membedakan diri dengan pelayanan luar...

Харьковский уезд Страна Российская империя Губерния Харьковская губерния Уездный город Харьков История и география Дата образования 1780 Дата упразднения 1923 Площадь 2905,1 вёрст² Население Население 348 488[1] (1897) чел. Харьковский уезд — административно-террит...
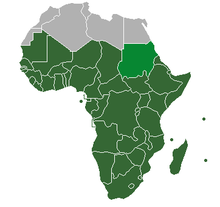
Region south of the Sahara Desert PlaceSub-Saharan AfricaGeographical map of sub-Saharan Africa The Sahara The Sahel Sub-Saharan Africa Major citiesAbidjan, Abuja, Accra, Addis Ababa, Cape Town, Dar es Salaam, Durban, Harare, Johannesburg, Juba, Kampala, Kinshasa, Lagos, Luanda, Lusaka, Mogadishu, Nairobi, Pretoria, WindhoekPopulation (2021)[a]1,137,938,708DemonymsAfricanReligions (2020)[1] • Christianity62.0% • Is...

Не следует путать с распознаванием голоса. Распознавание речи — автоматический процесс преобразования речевого сигнала в цифровую информацию (например, текстовые данные). Обратной задачей является синтез речи (Text-To-Speech). Содержание 1 История 2 Классификация систем ра�...

Jayshree T.Jayshree T. pada Maret 2013LahirJayshree T.1953PekerjaanPemeranTahun aktif1968-sekarangSuami/istriJai Prakash Jayshree Talpade (kelahiran c. 1953) adalah seorang pemeran dan penari Marathi, yang berkarya dalam film Bollywood dan beberapa film Gujarat dan Marathi. Karier Talpade memulai kariernya pada usia 5 tahun pada 1958 dengan Goonj Uthi Shehnai.[1] Ia mendapatkan popularitas setelah tampil dalam beberapa lagu tari, menjadi seorang eksponen Kathak. Namun ia telah m...

County in New Mexico, United States County in New MexicoMcKinley CountyCountyMcKinley County Courthouse in GallupLocation within the U.S. state of New MexicoNew Mexico's location within the U.S.Coordinates: 35°35′N 108°16′W / 35.58°N 108.26°W / 35.58; -108.26Country United StatesState New MexicoFoundedJanuary 1, 1901Named forWilliam McKinleySeatGallupLargest cityGallupArea • Total5,455.5 sq mi (14,130 km2) • Land...

Русские лапти Почтовая марка России, 2017 год (ЦФА [АО «Марка»] № 2193) Лапти (бахилы) лыковые Мужик плетёт лапти. Лубок XVIII (?) века Сходный вид обуви применяли североамериканские индейцы — сандалии XII века Ла́пти, ед. ч. ла́поть[1] (лапото́к[2], ла́пик[2]...

Biblical figure For other uses, see Enos (disambiguation). Not to be confused with Enoch (ancestor of Noah). EnosEnos (Lyon Cathedral, stained glass window)Venerated inIslam and MandaeismSpouseNoam [1]ChildrenKenanmore sons and daughtersParentSeth (father)RelativesAdam and Eve (grandparents)Cain (uncle)Abel (uncle)Enoch (cousin)Mahalalel (grandson)Jared (great-grandson)Enoch (great-great-grandson)Methuselah (great-great-great-grandson)Lamech (great-great-great-great-grandson)Noah (great-...

Family of plants Lophiocarpaceae Corbichonia decumbens Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Order: Caryophyllales Family: LophiocarpaceaeDoweld & Reveal[1][2] Genera Corbichonia Lophiocarpus The Lophiocarpaceae are a family of flowering plants comprising mostly succulent subshrubs and herbaceous species native to tropical to southern sub-Saharan Africa to western India. It includes the genera Corbichonia and Lop...

Malian footballer (born 1991) Moussa Marega Marega with Porto in 2018Personal informationFull name Moussa Marega[1]Date of birth (1991-04-14) 14 April 1991 (age 33)Place of birth Les Ulis, FranceHeight 1.84 m (6 ft 0 in)[2]Position(s) Second strikerTeam informationCurrent team SharjahNumber 91Youth career2006–2010 ÉvrySenior career*Years Team Apps (Gls)2010–2011 Évry 4 (0)2011–2012 FC Issy 0 (0)2012–2013 Le Poiré-sur-Vie 31 (5)2013 Le Poiré-sur-...

Ritual bowl for libation For other uses, see Patera (disambiguation). Patera from Georgia, likely depicting Fortuna (2nd century AD,[1] Georgian National Museum) In the material culture of classical antiquity, a patera (Latin pronunciation: [ˈpatɛra]) or phiale (Ancient Greek: φιάλη [pʰi.á.lɛː])[2] is a shallow ceramic or metal libation bowl. It often has a bulbous indentation (omphalos, belly button) in the center underside to facilitate holding it,...
Olympic sport Single scullsat the Olympic GamesMedal ceremony of the men's single sculls in 2016OverviewSportRowingGenderMen and womenYears heldMen: 1900–2020Women: 1976–2020Reigning championMen Stefanos Ntouskos (GRE)Women Emma Twigg (NZL) The single sculls is a rowing event held at the Summer Olympics. The event was first held for men at the second modern Olympics in 1900, and has been held every Games since. The women's competition was added in 1976. Medalists Men G...

Universitas Duisburg-EssenRektorProf. Dr. Ulrich Radtke Sebuah gedung Uni-DUE di Campus Essen Universitas Duisburg-Essen (dalam bahasa Jerman: Universität Duisburg-Essen) adalah sebuah universitas di Jerman yang terletak di negara bagian Nordrhein-Westfalen. Universitas ini merupakan hasil gabungan dari Universitas Gerhard Mercator, Duisburg dan Universitas Essen pada 1 Januari 2003. Sebelumnya kedua universitas tersebut telah berdiri sejak tahun 1972. Dengan memiliki 12 fakultas dan lebih d...

Georgia Artikel ini adalah bagian dari seri Politik dan KetatanegaraanGeorgia Konstitusi Mahkamah Konstitusi Hak asasi manusia Hak LGBT Eksekutif Presiden (daftar) Salome Zourabichvili Perdana Menteri Irakli Garibashvili Legislatif Parlemen Ketua: Shalva Papuashvili Yudikatif Mahkamah Agung Pembagian Administratif Mkhare (Region) Munisipalitas Republik Otonom Pemilihan umum Pemilihan umum terakhir Parlemen: 20122016 Presiden: 20082013 Partai politik Hubungan luar negeri Dengan Uni Eropa Denga...

Wilderness area in Oregon, United States Oregon Badlands WildernessIUCN category Ib (wilderness area)Oregon Badlands with sagebrush in bloom, Juniper trees, and proximity to Oregon CascadesLocationDeschutes / Crook counties, Oregon, United StatesNearest cityBend, OregonCoordinates44°00′N 121°02′W / 44°N 121.04°W / 44; -121.04Area29,301 acres (11,858 ha)EstablishedUnited States Bureau of Land Management The Oregon Badlands Wilderness is a 29,301-acre (...

Government-sanctioned killing Part of a series onGenocide Issues List of genocides Genocides in history Effects on youth Denial Massacre Rape Incitement In relation to Colonialism / War Perpetrators, victims, and bystanders Prevention Psychology Recognition politics Risk factors Stages Types Anti-Indigenous Cultural Utilitarian Studies Outline Bibliography Related topics Compulsory sterilization Democide Ethnic cleansing Ethnocide Forced assimilation Categoryvte Democide refers to th...

American politician Elias S. HolidayMember of the U.S. House of Representativesfrom Indiana's 5th districtIn officeMarch 4, 1901 – March 4, 1909Preceded byGeorge W. FarisSucceeded byRalph Wilbur Moss Personal detailsBornElias Selah Holiday(1842-03-05)March 5, 1842Aurora, Illinois, U.S.DiedMarch 13, 1936(1936-03-13) (aged 94)Brazil, IndianaPolitical partyRepublicanResidenceBrazil, IndianaEducationHartsville CollegeMilitary serviceAllegianceUnion ArmyRankFirst sergea...

Joost Eerdmans Bernard Johannes (Joost) Eerdmans (lahir 9 Januari 1971 di Harderwijk) adalah seorang politikus Belanda. Sebagai anggota LPF, dia adalah anggota Dewan Perwakilan dari 23 Mei 2002 sampai 30 November 2006 dan sebagai anggota JA21, dia adalah anggota Dewan Perwakilan sejak 31 Maret 2021. Eerdmans dan Annabel Nanninga didirikan JA21 pada 18 Desember 2020. Dari 2009 sampai 2014 ia adalah anggota dewan harian munisipalitas Capelle aan den IJssel. Dari 2014 sampai 2018 ia adalah anggo...

В Википедии есть статьи о других людях с такой фамилией, см. Клубов. Александр Фёдорович Клубов Дата рождения 18 января 1918(1918-01-18)[1] Место рождения деревня Яруново, Вологодский уезд, Вологодская губерния, Советская Россия Дата смерти 1 ноября 1944(1944-11-01)[1] (26 лет) Мес...

Bahasa Korea Pertengahan WilayahSemenanjung Korea dan ManchuriaEraAbad ke-11 sampai ke-16, kemudian berkembang menjadi bahasa Korea Modern Rumpun bahasaKoreanik Korea Pertengahan Bentuk awalProto-Koreanik Korea KunoKorea Pertengahan Sistem penulisanIdu, Hyangchal, Gugyeol, HangeulKode bahasaISO 639-3okmLINGUIST List okmGlottolog[1]IETFokm Status pemertahanan Punah EXSingkatan dari Extinct (Punah)Terancam CRSingkatan dari Critically endangered (Terancam Kritis) SESingkatan dari Severely endang...