142 857
| |||||||||||||||||||||||||||||||||||||
Read other articles:

WTVJMiami / Fort Lauderdale, FloridaSaluranAnalog: 6 (VHF)Digital: 31 (UHF)BrandingNBC 6 (umum)NBC 6 News (berita)SloganSouth Florida'sNews LeaderPemrogramanAfiliasiNBC (sekunder 1949-56; dasar 1989-sekarang)NBC WX+ (on DT2)KepemilikanPemilikNBC Universal(sale to Post-Newsweek Stations pending approval) (NBC Telemundo License Company)Stasiun seindukWSCVRiwayatSiaran perdana21 Maret 1949Bekas nomor kanal4 (1949-1995)Bekas afiliasiCBS (waktu penuh 1949-1989)ABC (sekunder 1949-1957)DuMont (sekun...

Grand Prix Valencia 2016Detail lombaLomba ke 18 dari 18Grand Prix Sepeda Motor musim 2016Tanggal13 November 2016Nama resmiGran Premio Motul de la Comunitat Valenciana[1][2][3]LokasiCircuit Ricardo Tormo, Valencia, SpanyolSirkuitFasilitas balapan permanen4.005 km (2.489 mi)MotoGPPole positionPembalap Jorge Lorenzo YamahaCatatan waktu 1:29.401 Putaran tercepatPembalap Jorge Lorenzo YamahaCatatan waktu 1:31.171 di lap 5 PodiumPertama Jorge Lorenzo Ya...

العلاقات البولندية الكازاخستانية بولندا كازاخستان بولندا كازاخستان تعديل مصدري - تعديل العلاقات البولندية الكازاخستانية هي العلاقات الثنائية التي تجمع بين بولندا وكازاخستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للد�...

This article is about the receptacle in botany. For other uses, see Receptacle. In botany, the receptacle refers to vegetative tissues near the end of reproductive stems that are situated below or encase the reproductive organs. Angiosperms AngiospermsThe receptacle (grey) in relation to the ovary (red) in three types of flowers: hypogynous (I), perigynous (II), and epigynous (III) In angiosperms, the receptacle or torus (an older term is thalamus, as in Thalamiflorae) is the thickened part o...

Tomsk State University of Control Systems and RadioelectronicsТомский государственный университет систем управления и радиоэлектроникиEstablished1962RectorVictor RulevskiyAcademic staff970Students11,000LocationTomsk, RussiaWebsitehttp://www.tusur.ru/en/ University rankingsRegional – OverallQS Emerging Europe and Central Asia[1]231-240 (2022) Tomsk State University of Control Systems and Radioelectronics (Russian: То...

Ancient temple in Agrigento, Italy Not to be confused with Temple of Concord. Temple of ConcordiaAlternative namesTemple of ConcordGeneral informationArchitectural styleAncient GreekLocationAgrigento, Sicily, ItalyCompletedc. 440-430 BC[1][2]Renovated1785AffiliationChristian church (6th century-1785)Height8.93 m (29.3 ft)[3]DimensionsOther dimensions39.42 m × 16.92 m (129.3 ft × 55.5 ft)[1][4] The Temple o...

Association football club in Stevenage, England Stevenage Borough redirects here. For the council, see Stevenage Borough Council. Football clubStevenageFull nameStevenage Football ClubNickname(s)The BoroFounded1976; 48 years ago (1976)(as Stevenage Borough F.C.)GroundThe Lamex StadiumCapacity7,800ChairmanPhil Wallace[1]ManagerAlex Revell (interim)LeagueEFL League One2023–24EFL League One, 9th of 24WebsiteClub website Home colours Away colours Third colours Current ...

سباستيان لارسون (بالسويدية: Sebastian Larsson) معلومات شخصية الاسم الكامل ألفي إنجي سباستيان لارسون الميلاد 6 يونيو 1985 (العمر 38 سنة)[1]إسكليستونا الطول 1.78 م (5 قدم 10 بوصة) مركز اللعب وسط الجنسية السويد معلومات النادي النادي الحالي أيك سولنا الرقم 7 مسيرة الشباب سن�...

Ed Groot Vincentius Aloysius (Ed) Groot (lahir 26 Desember 1957) adalah seorang politikus Belanda dan mantan wartawan, kolumnis dan pegawai negeri. Sebagai anggota Partai Buruh (Partij van de Arbeid), ia menjadi anggota parlemen antara 17 JUni 2010 dan 23 Maret 2017.[1] Ia berfokus pada materi-materi perpajakan, penjalanan pemerintahan dan keuangan. Referensi ^ Drs. V.A. (Ed) Groot (dalam bahasa Dutch). Parlement.com. Diakses tanggal 8 April 2017. Pemeliharaan CS1: Bahasa yang ti...
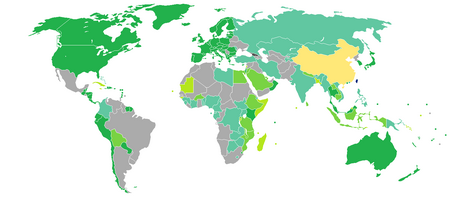
提示:此条目页的主题不是中國—瑞士關係。 關於中華民國與「瑞」字國家的外交關係,詳見中瑞關係 (消歧義)。 中華民國—瑞士關係 中華民國 瑞士 代表機構駐瑞士台北文化經濟代表團瑞士商務辦事處代表代表 黃偉峰 大使[註 1][4]處長 陶方婭[5]Mrs. Claudia Fontana Tobiassen 中華民國—瑞士關係(德語:Schweizerische–republik china Beziehungen、法�...

Amsal 9Kitab Amsal lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab AmsalKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen20← pasal 8 pasal 10 → Amsal 9 (disingkat Ams 9) adalah bagian dari Kitab Amsal dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen.[1][2] Teks Naskah sumber utama: Masoretik, Septuaginta dan Naskah Laut Mati. Pasal ini terdiri dari 18 ayat. Berisi nasihat-nasihat yang diucapkan oleh raja Salomo bin...

Type of unemployment This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Frictional unemployment – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Frictional unemployment is a form of unemployment reflecting the gap between someone voluntarily leaving a job...

Intergovernmental organisation British–Irish CouncilComhairle na Breataine–na hÉireannLogo of the British–Irish CouncilHeads of government meet in Glasgow for the 26th council summitAbbreviationBICFormation2 December 1999; 24 years ago (1999-12-02)TypeIntergovernmental organisationHeadquartersEdinburgh, Scotland (secretariat)Coordinates55°56′45″N 3°13′21″W / 55.94584°N 3.22262°W / 55.94584; -3.22262Region served British IslesMembers...

Cet article est une ébauche concernant une élection ou un référendum luxembourgeois. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. 1918 1922 Élections législatives luxembourgeoises de 1919 48 sièges de la Chambre des députés(Majorité absolue : 25 sièges) 26 octobre 1919 Type d’élection Élections législatives Corps électoral et résultats Population 261 643[2] Inscrits 126 1...

In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of some defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci – in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane i...

Kolkata Municipal Corporation in West Bengal, IndiaWard No. 13Kolkata Municipal CorporationInteractive Map Outlining Ward No. 13Ward No. 13Location in KolkataCoordinates: 22°35′39″N 88°23′09″E / 22.594167°N 88.385889°E / 22.594167; 88.385889Country IndiaStateWest BengalCityKolkataNeighbourhood coveredUltadanga (Daspara-Muchi Bazar-Telenga Bagan-Surir Bagan)ReservationOpenParliamentary constituencyKolkata UttarAssembly constituencyManiktalaBorough3Popu...

Stadium in Auckland, New Zealand This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Western Springs Stadium – news · newspapers · books · scholar · JSTOR (June 2016) (Learn how and when to remove this message) Western Springs StadiumLocationStadium Rd, Western Springs, Auckland, New ZealandCoordinates36°51′5...

2005 withdrawal of Israeli personnel Map of the Gaza Strip in May 2005, a few months prior to the Israeli withdrawal. The major settlement blocs were the blue-shaded regions of this map. Part of a series onthe Israeli–Palestinian conflictIsraeli–Palestinianpeace process HistoryCamp David Accords1978Madrid Conference1991Oslo Accords1993 / 95Hebron Protocol1997Wye River Memorandum1998Sharm El Sheikh Memorandum1999Camp David Summit2000The Clinton Parameters2000Taba Summit2001Road Ma...

Герб Руського воєводства (кінець 16 століття). У Вікіпедії є статті про інші значення цього терміна: Воєвода (значення). Ру́ський воєво́да (лат. Palatinus Russiae; пол. wojewoda ruski) — уряд (посада) очільника Руського воєводства в Королівстві Польському та Речі Посполитій. Існувала пр�...

Eclissi solare del 3 gennaio 1927MappaTipoAnulare Gamma-0.4956 Magnitudine0.9995 Coordinate eclissi massima52.8°S 124.8°W Orari (UTC)Eclissi massima20:22:53 L'eclissi solare del 3 gennaio 1927 è un evento astronomico che ha avuto luogo il suddetto giorno attorno alle ore 20.22 UTC.[1] L'eclissi, di tipo anulare, è passata attraverso la Nuova Zelanda, Cile, Argentina, Uruguay e Brasile, mentre l'eclissi solare parziale ha coperto il Pacifico centrale e meridionale, la maggior p...















