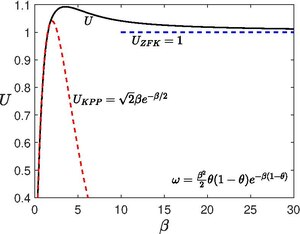
ZFK equation
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Chen YangChen Yang memegang medali emas pada 2017Informasi pribadiKewarganegaraanTiongkokLahir10 Juli 1991 (umur 32)Tinggi180 m (590 ft 6+1⁄2 in)[1]Berat97 kg (214 pon)[1] OlahragaOlahragaTrek dan la...

Standar TV melalui 1080p. Gambar berwarna merah menunjukkan resolusi 576i atau 576p. Gambar berwarna biru menunjukkan resolusi 720p, tingkat resolusi HDTV. Gambar penuh warna menunjukkan resolusi 1080p. Logo Full HD 1080p 1080p (1920 × 1080 px; juga dikenal sebagai Full HD atau FHD dan BT.709) adalah satu set mode video HDTV definisi tinggi yang ditandai dengan 1080 garis horizontal resolusi vertikal.[1] Kepanjangan dari p adalah pemindaian progresif, yaitu non-interlaced. Istilah in...

العلاقات البنمية التشيلية بنما تشيلي بنما تشيلي تعديل مصدري - تعديل العلاقات البنمية التشيلية هي العلاقات الثنائية التي تجمع بين بنما وتشيلي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة بنما تشيلي المس�...

Global network of research-intensive universities Universitas 21Formation1997TypeEducation and researchHeadquartersBirmingham, United KingdomRegion served GlobalProvostJenny DixonWebsiteU21 Universitas21 Universitas 21 (U21) is an international network of research-intensive universities.[1][2][3] Founded in Melbourne, Australia in 1997 with 11 members, it has grown to include twenty-nine member universities in nineteen countries and territories.[4][5] T...

Chronologies File d'attente devant une boulangerie-pâtisserie à Paris au printemps 1945.Chronologie de la Seconde Guerre mondiale Jan - Fév - Mar - Avr - Mai - Juin Juil - Aoû - Sep - Oct - Nov - Déc Chronologie dans le monde 1942 1943 1944 1945 1946 1947 1948Décennies :1910 1920 1930 1940 1950 1960 1970Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Al...

Cet article est une ébauche concernant le catch. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (septembre 2008). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualit...

Halaman ini berisi artikel tentang musikal. Untuk rekaman pemeran Broadway, lihat Hamilton (album). HamiltonAn American MusicalPlaybill dari Original Broadway ProductionMusikLin-Manuel MirandaLirikLin-Manuel MirandaNaskahLin-Manuel MirandaDiangkat dariAlexander Hamiltonkarya Ron ChernowDebut20 Januari 2015 – The Public Theater, New York CityProduksi2015 Off-Broadway2015 BroadwayPenghargaanDaftar penghargaan Drama Desk Award for Outstanding Musical Drama Desk Award for Outstanding Music...

1991 video game 1991 video gameThe Legend of Zelda: A Link to the PastNorth American box artDeveloper(s)Nintendo EADPublisher(s)NintendoDirector(s)Takashi TezukaProducer(s)Shigeru MiyamotoProgrammer(s) Yasunari Soejima Toshihiko Nakago Artist(s) Masanao Arimoto Tsuyoshi Watanabe Writer(s) Kensuke Tanabe Composer(s)Koji KondoSeriesThe Legend of ZeldaPlatform(s)Super NESReleaseJP: November 21, 1991NA: April 13, 1992EU: September 24, 1992Genre(s)Action-adventureMode(s)Single-player The Legend of...

Portugalau Concours Eurovision 2022 Données clés Pays Portugal Chanson Saudade, saudade Interprète MARO Langue Portugais, anglais Sélection nationale Radiodiffuseur RTP Type de sélection Festival da Canção 2022 Date 12 mars 2022 Concours Eurovision de la chanson 2022 Position en demi-finale 4e (208 points, qualifiée) Position en finale 9e (207 points) 2021 2023 modifier Le Portugal est l'un des quarante pays participants du Concours Eurovision de la chanson 2022, qui ...

International song competition Eurovision Song Contest 1983DatesFinal23 April 1983HostVenueRudi-Sedlmayer-HalleMunich, West GermanyPresenter(s)Marlene CharellMusical directorDieter ReithDirected byRainer BertramExecutive supervisorFrank NaefExecutive producerChristian HayerGünther LebramHost broadcasterArbeitsgemeinschaft der öffentlich-rechtlichen Rundfunkanstalten der Bundesrepublik Deutschland (ARD)Bayerischer Rundfunk (BR)Websiteeurovision.tv/event/munich-1983 ParticipantsNumber of entr...

Alphabetical list of named rocks and meteorites found on Mars Martian rocks redirects here. For Martian meteorites found on Earth, see List of Martian meteorites. This is an alphabetical list of named rocks (and meteorites) found on Mars, by mission. This list is a sampling of rocks viewed, and is not an exhaustive listing. A more complete listing may be found on the various NASA mission web sites. This listing does not include Martian meteorites found on Earth. Names for Mars rocks are large...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Miamisburg, Ohio – news · newspapers · books · scholar · JSTOR (June 2016) (Learn how and when to remove this message) City in Ohio, United StatesMiamisburg, OhioCityMain Street in MiamisburgNickname(s): Hole's Station, The BurgMotto: Ohio's Star Cit...

Japanese racing driver Shigeaki HattoriNationalityJapaneseBorn (1963-11-03) November 3, 1963 (age 60)Okayama, OkayamaRetired2005Indy Racing League IndyCar SeriesYears active2000–2003TeamsTreadway-Vertex Cunningham RacingBradley MotorsportsA. J. Foyt EnterprisesStarts26Wins0Poles0Best finish13th in 2001Previous series19991996–19981993–1994CART World SeriesIndy LightsAll-Japan Formula Three ChampionshipNASCAR driver NASCAR Craftsman Truck Series career10 races run over 1 yearBest fin...

He Was CoolPoster film He Was CoolNama lainHangul그 놈은 멋있었다 Alih Aksara yang DisempurnakanGeu nomeun meoshisseotdaMcCune–ReischauerKŭ nomŭn mŏtissiŏtta SutradaraLee Hwan-gyeongProduserGwak Jeong-HwanSkenarioLee Hwan-GyeongBerdasarkanNovelGuiyeoniPemeranSong Seung HunJung Da BinPenata musikAhn Jeong-HunSinematograferLee Gang-MinPenyuntingKim Seon-MinDistributorHapdong FilmsTanggal rilis 22 Juli 2004 (2004-07-22) Durasi113 menitBahasaKorea He Was Cool (그 �...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Finnish technology company making measuring instruments For other uses, see Vaisala (disambiguation). Second Wind (company) redirects here. For the gaming journalism outlet, see Second Wind (entertainment group). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and in...

Mathematical model of a thin, flat object This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Planar lamina – news · newspapers · books · scholar · JSTOR (Octo...

American businessman Samuel J. PalmisanoPalmisano in March 2013Born (1951-07-29) July 29, 1951 (age 72) [1]Baltimore, Maryland, U.S.EducationBachelor of Arts (1973)Alma materJohns Hopkins UniversityYears active1973–presentEmployerIBM (1973–2012)TitleChairmanPredecessorLouis V. Gerstner, Jr.SuccessorVirginia M. RomettyBoard member ofIBM Corporation, 2000ExxonMobil Corp., 2006Spouse(s)Gaier Notman, known as MissyChildrenthree sons, one daughterWebsiteIBM - Samuel...

Mitos Kecantikan Sampul edisi IndonesiaPengarangNaomi WolfBahasaInggrisPenerbitChatto & WindusTanggal terbit1990Jenis mediaPrintISBNISBN 978-0-385-42397-7Diikuti olehFire with Fire: The New Female Power and How To Use It Mitos Kecantikan: Kala Kecantikan Menindas Perempuan adalah sebuah buku nonfiksi karya Naomi Wolf, diterbitkan pada tahun 1990 oleh Chatto & Windus di Inggris dan William Morrow & Co (1991) di Amerika Serikat. Lalu diterbitkan ulang pada tahun...

لمعانٍ أخرى، طالع سيبيريا (توضيح). سيبيريا تعديل مصدري - تعديل سيبيريا هي إحدى قارات العالم القديم واليوم أصبحت الجزء الشرقي والشمال الشرقي من روسيا، حيث كانت قارة مستقلة قبل العصر البرمي. يمتد غرباً من جبال الأورال حتى المحيط الهادي شرقاً، ومن المحيط المتجمد...



![{\displaystyle \theta \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)