Yao's Millionaires' problem
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Ryszard KotysRyszard Kotys pada 2009Lahir(1932-03-20)20 Maret 1932Mniów, PolandiaMeninggal28 Januari 2021(2021-01-28) (umur 88)Poznań, PolandiaPekerjaanPemeranTahun aktif1953–2021 Ryszard Kotys (20 Maret 1932 – 28 Januari ...

Untuk kegunaan lain, lihat Portland Timbers. Portland TimbersJulukanThe TimbersBerdiri20 Maret 2009; 14 tahun lalu (2009-03-20)[nb 1]StadionProvidence ParkPortland, Oregon(Kapasitas: 25,218)PemilikPeregrine SportsPresidenMerritt PaulsonPelatih kepalaGiovanni SavareseLigaMajor League Soccer2021Wilayah barat: ke-4Keseluruhan: ke-5Play-off: Runner-upSitus webSitus web resmi klub Kostum kandang Kostum tandang Musim ini Portland Timbers FC adalah klub sepak bola profesional Ameri...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Bartine Burkett ZaneBartine Burkett di The High Sign (1921)Lahir(1898-02-09)9 Februari 1898Robeline, Louisiana, A.S.Meninggal20 Mei 1994(1994-05-20) (umur 96)Burbank, California, A.S.PekerjaanAktrisTahun aktif1917–1983Suami/istriRalph Zane...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

2014 American found footage horror film by Grégory Levasseur This article is missing information about the film's production. Please expand the article to include this information. Further details may exist on the talk page. (September 2019) This article is about the American film. For the Russian film, see The PyraMMMid. The PyramidTheatrical release posterDirected byGrégory LevasseurWritten byDaniel MeersandNick SimonProduced byAlexandre AjaMark CantonChady Eli MattarScott C. SilverStarri...

Cette chronologie est une ébauche concernant la science. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Données clés 2005 2006 2007 2008 2009 2010 2011Décennies :1970 1980 1990 2000 2010 2020 2030Siècles :XIXe XXe XXIe XXIIe XXIIIeMillénaires :Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Béni...

Perhimpunan Bangsa-Bangsa Asia Tenggara Burmaအရှေ့တောင်အာရှနိုင်ငံများအသင်းFilipino:Samahán ng mga Bansâ sa Timog Silangang Asya[1]Indonesia:Perhimpunan Bangsa-bangsa Asia Tenggara[2]Khmer:សមាគមប្រជាជាតិអាស៊ីអាគ្នេយ៍Lao:ສະມາຄົມປະຊາຊາດແຫ່ງອາຊີຕະເວັນອອກສຽງໃຕ້Melayu:Persatuan Negara-negara As...

هذه المقالة عن جمهورية العراق. لمعانٍ أخرى، طالع العراق (توضيح). العراق جمهورية العراقكۆماری عێراق (كردية) العراقعلم العراق العراقشعار العراق العراق الشعار الوطنيالله أكبر النشيد: موطني[1] الأرض والسكان إحداثيات 33°N 43°E / 33°N 43°E / 33; 43 [2&...

Tina Smith Senator Amerika Serikat dari MinnesotaPetahanaMulai menjabat 3 Januari 2018Menjabat bersama Amy KlobucharDitunjuk olehMark Dayton PendahuluAl FrankenPenggantiPetahanaWakil Gubernur Minnesota ke-48Masa jabatan5 Januari 2015 – 2 Januari 2018GubernurMark Dayton PendahuluYvonne Prettner SolonPenggantiMichelle Fischbach Informasi pribadiLahirChristine Elizabeth Flint[1]4 Maret 1958 (umur 66)Albuquerque, New Mexico, Amerika SerikatPartai politikPartai ...

Untuk aktor dengan nama yang mirip, lihat Alec Baldwin. Adam BaldwinAdam BaldwinLahir27 Februari 1962 (umur 62)Winnetka, Illinois, U.S.PekerjaanAktorTahun aktif1980–sekarangSuami/istriAmi Julius (m. 1988)Anak3 Adam Baldwin (lahir 27 Februari 1962) adalah seorang aktor Amerika. Dia membintangi Full Metal Jacket (1987) sebagai Ibu Hewan, serta di serial televisi Firefly dan film lanjutannya Serenity sebagai Jayne Cobb. Perannya termasuk Stillman di Ord...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

لمعانٍ أخرى، طالع فتح المتعال (توضيح). فتح المتعال في مدح النعال فَتْحُ الْمُتَعَال فِي مِدْحِ النِّعَال معلومات الكتاب المؤلف أحمد المقري التلمساني البلد مصر اللغة العربية الناشر دار الكتب العلمية تاريخ النشر 2006 الموضوع السيرة النبوية التقديم عدد الص...

Nahum GoldmannNahum GoldmannNama asal נחום גולדמןLahir(1895-07-10)10 Juli 1895Vishnevo, Kekaisaran Rusia(kini Vishnyeva, Belarus)Meninggal29 Agustus 1982(1982-08-29) (umur 87)Bad Reichenhall, JermanDikenal atasPendiri dan presiden Kongres Yahudi Sedunia Nahum Goldmann (Ibrani: נחום גולדמן) (10 Juli 1895 – 29 Agustus 1982) adalah seorang Zionis utama. Ia adalah pendiri Kongres Yahudi Sedunia dan presidennya dari 1951 sampai 1978, dan juga meru...

Period of reduced funding and interest in AI research Part of a series onArtificial intelligence Major goals Artificial general intelligence Recursive self-improvement Planning Computer vision General game playing Knowledge reasoning Machine learning Natural language processing Robotics AI safety Approaches Symbolic Deep learning Bayesian networks Evolutionary algorithms Situated approach Hybrid intelligent systems Systems integration Applications Projects Deepfake Machine translation Generat...
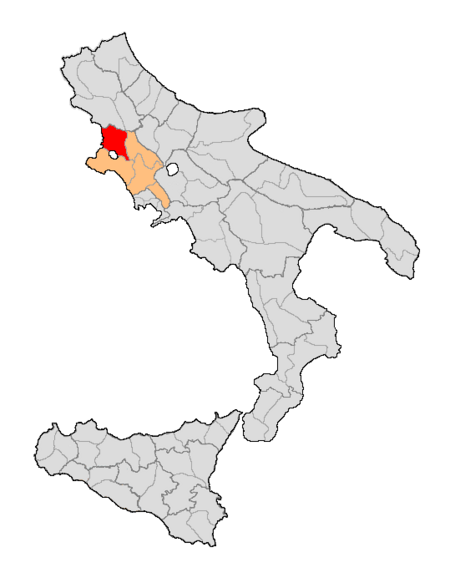
Voci principali: Storia di Sora, Sora (Italia). Distretto di SoraInformazioni generaliCapoluogoSora Dipendente da Terra di Lavoro Suddiviso in8 Circondari39 comuni16 villaggi AmministrazioneOrgani deliberativiSottintendenteConsiglio distrettuale Evoluzione storicaInizio1806 con Antonio Siciliani CausaL. 132 del 1806 del Regno di Napoli Fine1860 CausaOccupazione garibaldina e annessione al Regno di Sardegna. Preceduto da Succeduto da Circondario di Sora Cartografia Il distretto di Sora fu una...

此條目没有列出任何参考或来源。 (2013年2月8日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 莱奥波尔多·加尔铁里Leopoldo Fortunato Galtieri Castelli 阿根廷总统(實質)任期1981年12月22日—1982年6月18日副总统Víctor Martínez前任卡洛斯·拉科斯特继任阿尔弗雷多·奥斯卡·圣琼 个人资料出生(1926-07-15)1926�...

نوغةمعلومات عامةالمنشأ الشرق الأوسط النوع حلويات المكونات الرئيسية سكر تعديل - تعديل مصدري - تعديل ويكي بيانات النوغة (وتكتب أيضا النوجة) هي نوع من الحلوى مصنوعة من السكر و/أو العسل مع المكسرات المحمصة (لوز، فستق، جوز، مكاداميا) وأحيانا تحتوي بعض الفواكة المجففة.[1][2 ...
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Road signs in Iceland – news · newspapers · books · scholar · JSTOR (December 2018) (Learn how and when to ...

2004 American science fiction television series Battlestar GalacticaGenre Military science fiction Political drama[1][2][3] Post-apocalyptic Space opera Based onBattlestar Galacticaby Glen A. LarsonDeveloped byRonald D. MooreStarring Edward James Olmos Mary McDonnell Katee Sackhoff Jamie Bamber James Callis Tricia Helfer Grace Park Michael Hogan Aaron Douglas Tahmoh Penikett Paul Campbell Nicki Clyne Michael Trucco Alessandro Juliani Kandyse McClure Opening themeGayatr...

First Nations government Map of Nanoose First Nation TerritoryThe Nanoose First Nation, also known the Snaw-naw-as First Nation,[1] is a First Nations government located on central Vancouver Island in southwestern British Columbia, Canada, in the vicinity of the community of Nanoose Bay. They are Coast Salish people, and one of the most northern tribes on the east side of Vancouver Island. They speak Hul’q’umi’num’, which is 1 of 3 branches of the Halkomelem dialect spoken fro...









































































