Von Kármán wind turbulence model
|
Read other articles:

Gymnocranius Gymnocranius griseus Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Perciformes Famili: Lethrinidae Subfamili: Monotaxinae Genus: GymnocraniusKlunzinger, 1870 Spesies tipe Dentex rivulatusRüppell, 1838 Spesies Lihat teks Sinonim Paradentex Bleeker, 1872 Gymnocranius adalah genus ikan lencam yang berasal dari Samudera Hindia dan Samudera Pasifik bagian barat. Daftar Spesies[1] Gymnocranius audleyi J. D. Ogilby, 1916[1]...

Gua Kizil克孜尔千佛洞Gua KizilLokasi di XinjiangLokasiXinjiang, ChinaKoordinat41°47′N 82°30′E / 41.783°N 82.500°E / 41.783; 82.500Koordinat: 41°47′N 82°30′E / 41.783°N 82.500°E / 41.783; 82.500 Gua Kizil Nama Tionghoa Hanzi sederhana: 克孜尔千佛洞 Hanzi tradisional: 克孜爾千佛洞 Makna harfiah: Gua Seribu Buddha Kizil Alih aksara Mandarin - Hanyu Pinyin: Kèzī'ěr Qiānfú Dòng Nama Uighur Uighur: قىزىل م...

Museum AdityawarmanMuseum Nagari AdityawarmanDidirikan1977LokasiJl. Diponegoro No. 10, Belakang Tangsi, Padang Barat, Padang, IndonesiaJenisMuseum daerahUkuran koleksi6.000DirekturMardison, S.Pd., M.Pd. (Kepala UPTD Museum)[1]KuratorGubernur dan Wakil Gubernur Sumatera Barat[2]Situs webmuseumadityawarman.org Museum Adityawarman adalah museum budaya Sumatera Barat yang terletak di Kota Padang.[3] Museum ini diresmikan pada 16 Maret 1977 mengambil nama besar salah seoran...

Chronologies Couverture du Petit Journal, supplément illustré du 16 mai 1897, numéro 339, Incendie du Bazar de la Charité, le sinistre.Données clés 1894 1895 1896 1897 1898 1899 1900Décennies :1860 1870 1880 1890 1900 1910 1920Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, ...

4th century BCE emperor of the Indian Nanda Empire Mahapadma NandaA silver coin of 1 karshapana of King Mahapadma Nanda or his sons 4th century BCE1st Nanda EmperorReignc. 345 BC – 329 BCPredecessorMahanandinSuccessorPandukaDied329 BCEIssue8 sons (including Dhana)DynastyNandaFatherMahanandin Mahapadma Nanda (IAST: Mahāpadmānanda; c. mid 4th century BCE), (died 329 BCE) according to the Puranas, was the first Emperor of the Nanda Empire of ancient India. The Puranas describe him as a...

Buster WarenskiBorn(1942-06-05)June 5, 1942Kimberly, Nevada, U.S.DiedJuly 31, 2005(2005-07-31) (aged 63)Richfield, Utah, U.S.Occupation(s)Knifemaker, bladesmithSpouseJulie Warenski Art knife by Warenski Buster Warenski (June 5, 1942 – July 31, 2005) was an American custom knifemaker from Kimberly, Nevada who made Art Knives utilizing gold and other precious metals. Warenski is best known for making a reproduction of Tutankhamun's dagger with a forged gold blade; over 32 ounces of gold ...

51st season in existence of Paris Saint-Germainقالب:SHORTDESC:51st season in existence of Paris Saint-Germain باريس سان جيرمانموسم 2020–21الرئيسناصر الخليفيالمدربتوماس توخل(حتى 29 ديسمبر)ماوريسيو بوتشيتينو(ابتداء من 2 يناير)الملعببارك دي برينسالدوري الفرنسيالثانيكأس فرنساالفائزكأس الأبطال الفرنسيالفائزدوري أبطال أور...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mzymta – news · newspapers · books · scholar · JSTOR (May 2020) (Learn how and when to remove this template message) River in Krasnodar Krai * Adlersky City District of Sochi, RussiaMzymta RiverMzymta from Maidens' Eyewater waterfallShow map of Krasnodar KraiSh...

Mustafa al-Kadhimiمصطفى الكاظميAl-Kadhimi pada Mei 2020 Perdana Menteri Irak ke-50Masa jabatan6 Mei 2020 – 28 Oktober 2022PresidenBarham SalihPendahuluAdil Abdul-MahdiPenggantiPetahanaMenteri Urusan Luar NegeriMasa jabatan12 Mei 2020 – 6 Juni 2020PendahuluMohamed Ali AlhakimPenggantiFuad HusseinDirektur INISMasa jabatan7 Juni 2016 – 9 April 2020PresidenFuad Masum Barham SalihPerdana MenteriHaider al-Abadi Adil Abdul-MahdiPendahuluZuheir Fadel Abbas...

Яичниковая артериялат. arteria ovarica Кровоснабжение женских репродуктивных органов Снабжает яичники, матка Берёт начало Брюшная аорта Каталоги FMATA98 Яичниковая артерия — разновидность гонадной артерии у женщин. Снабжает кровью яичники и матку.[1] Содержание 1 Топог�...

Данио-рерио Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые рыбыИн�...

Chronologies Données clés 1997 1998 1999 2000 2001 2002 2003Décennies :1970 1980 1990 2000 2010 2020 2030Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

Portuguese singer and songwriter (born 1987) In this Portuguese name, the first or maternal family name is Vilar and the second or paternal family name is Braamcamp Sobral. Luísa SobralComMLuísa Sobral at the Eurovision Song Contest 2017 in KyivBackground informationBirth nameLuísa Vilar Braamcamp SobralBorn (1987-09-18) 18 September 1987 (age 36)Lisbon, PortugalGenrespopWebsiteluisasobral.comMusical artist Luísa Vilar Braamcamp Sobral ComM (Portuguese pronunciation: [luˈiz�...

For the homonymous party founded in 1976, see People's Party (Spain, 1976). Reformist Centre redirects here. For reformism in politics more generally, see Reformism. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and remo...

Indian politician (1914-2010) For other uses, see Jyoti Basu (disambiguation). ComradeJyoti Basu6th Chief Minister of West BengalIn office21 June 1977 – 5 November 2000Preceded byPresident's ruleSucceeded byBuddhadeb BhattacharjeeMember of the West Bengal Legislative AssemblyIn office1977–2001Preceded byNew constituencySucceeded bySonali GuhaConstituencySatgachhiaIn office1952–1972Preceded byNew constituencySucceeded byShiba Pada BhattacharjeeConstituencyBaranagar1st Deputy Chief Mi...
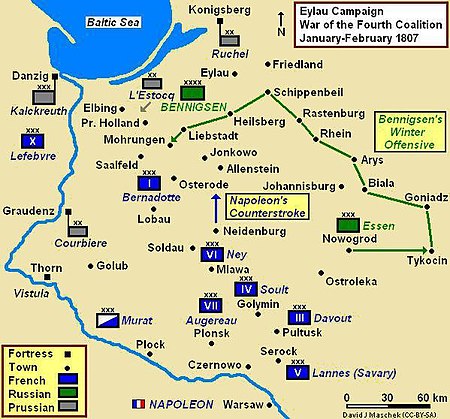
1807 Battle during the War of the Fourth Coalition For battles with the same name, see Battle of Ostrołęka. Battle of Ostrołęka (1807)Part of the War of the Fourth CoalitionMemorable combat of Ostrolenka, contemporary print in the Bibliothèque nationale de FranceDate16 February 1807[1]LocationOstrołęka, present-day Poland53°05′00″N 21°35′00″E / 53.083333°N 21.583333°E / 53.083333; 21.583333Result French victory[1]Belligerents French E...

بطولة باوليستا 1942 تفاصيل الموسم بطولة باوليستا البلد البرازيل البطل نادي بالميراس عدد المشاركين 11 بطولة باوليستا 1941 بطولة باوليستا 1943 تعديل مصدري - تعديل بطولة باوليستا 1942 هو موسم من بطولة باوليستا. أشرف على تنظيمه Federação Paulista de Futebol [الإنجليزية]&...

Practice of supernatural beings and forces This article is about beliefs and actions employed to influence supernatural beings and forces. For illusionism or stage magic, see Magic (illusion). The Magician, an illustration from the Rider–Waite tarot deck first published in 1910 Part of a series onMagic Background History of magic Magic and religion Psychological theories of magic Forms Apotropaic magic Black magic Ceremonial magic Chaos magic Divination Evocation Goetia Gray magic Invocatio...

HMAS Kanimbla pada 2010. Sebuah helikopter Sea King sedang mendarat di geladak belakangnya Sejarah United States Nama SaginawAsal nama City of Saginaw, MichiganPembangun National Steel & Shipbuilding CompanyPasang lunas 24 May 1969Diluncurkan 7 February 1970Sponsor Wife of R. James HarveyMulai berlayar 23 January 1971Dipensiunkan 28 June 1994Pelabuhan daftar Little Creek, VirginiaIdentifikasi LST-1188Nasib Transferred to the Royal Australian Navy in 1994 Australia Nama KanimblaAsal nama ...

Eleanor SangerSanger in 1961BornMary Eleanor Sanger(1929-09-15)September 15, 1929Hong KongDiedMarch 7, 1993(1993-03-07) (aged 63)Tisbury, MassachusettsNationalityAmericanEducationSmith College, Columbia UniversityKnown forTelevision Producer, Sports, WritingMovementWomen's Sports, Women in TelevisionAwards7 Emmy Awards, Smith College Medal Eleanor Sanger (September 15, 1929 – March 7, 1993) was a 7-time Emmy-award-winning television writer and producer, who was the first woman...





