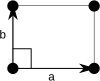
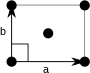
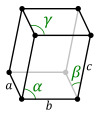
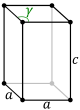
Unit cell
|
Read other articles:

Lac Wahapo Vue du lac depuis sa rive sud. Administration Pays Nouvelle-Zélande Subdivision District de Westland Géographie Coordonnées 43° 14′ 56″ S, 170° 15′ 58″ E Superficie 2,17 km2 Altitude 48 m Géolocalisation sur la carte : Nouvelle-Zélande Lac Wahapo modifier Le lac Wahapo (en anglais : Lake Wahapo et en maori de Nouvelle-Zélande : Wahapako) est un lac néo-zélandais situé dans le district de Westland, sur la Côte o...

3rd Algerian Infantry Division3e Division d'Infanterie AlgérienneThe insignia of the 3e DIA represents the winged statuette of the Victory of Cirta Victoire de Cirta with three crescentsActive1 May 1943 - 15 April 1946Country FranceAllegiance French ArmyTypeInfantry DivisionSize16,840 personnel (1943) 40% Europeans 60% Maghrebis Motto(s)It crescendoEngagementsItalian CampaignSouthern FranceVosges MountainsGambsheim BridgeheadBienwaldBadenCommandersNotablecommandersJoseph de Goislard de Monsa...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Final Carolingian-dynasty King of East Francia (reigned 900 to 911) For the king of Sicily with the same nickname, see Louis of Sicily. For the Chicago-based musical duo, see Louis the Child (DJs). Louis the ChildLouis the Child as he appears on the Imperial Sword.King of East FranciaReign899 – 20/24 September 911Coronation4 February 900, ForchheimPredecessorArnulf of CarinthiaSuccessorConrad IKing of LotharingiaReign900 – 20/24 September 911PredecessorZwentiboldSuccessorCharles I...

Humanist sans-serif font For other uses, see Verdana (disambiguation). VerdanaCategorySans-serifClassificationModern HumanistDesigner(s)Matthew CarterFoundryMicrosoft, Font Bureau (Verdana Pro)Date released1996Design based onTahomaVariationsMeiryoMS Reference Sans SerifNinaVerdana ProVerdana RefMetrically compatible withBitstream Vera SansDejaVu Sans Verdana is a humanist sans-serif typeface designed by Matthew Carter for Microsoft Corporation, with hand-hinting done by Thomas Rickner, then a...

Ability of an organism to sense water movements Arthropods like these northern prawn, and some mammals, detect water movement with sensory hairs such as whiskers, bristles or antennae In animal physiology, hydrodynamic reception refers to the ability of some animals to sense water movements generated by biotic (conspecifics, predators, or prey) or abiotic sources. This form of mechanoreception is useful for orientation, hunting, predator avoidance, and schooling.[1][2] Frequen...

Mountain in the state of Wyoming Fremont PeakFremont Peak at center from near Island LakeHighest pointElevation13,751 ft (4,191 m)[1]Prominence1,184 ft (361 m)[1]Coordinates43°07′29″N 109°37′05″W / 43.12472°N 109.61806°W / 43.12472; -109.61806[2]GeographyFremont PeakFremont / Sublette counties, Wyoming, U.S. Parent rangeWind River RangeTopo mapUSGS Fremont Peak SouthClimbingFirst ascent1842 Fremont and others...

梅拉蒂·达伊瓦·奥克塔维亚尼Melati Daeva Oktavianti基本資料代表國家/地區 印度尼西亞出生 (1994-10-28) 1994年10月28日(29歲)[1] 印度尼西亞万丹省西冷[1]身高1.68米(5英尺6英寸)[1]握拍右手[1]主項:女子雙打、混合雙打職業戰績48勝–27負(女雙)109勝–56負(混雙)最高世界排名第4位(混雙-普拉文·喬丹)(2020年3月17日[2])現時世界排名第...

«un esemplare di ciò che fu l’homo sapiens prima che la sapienza fosse peccato» (Eugenio Montale, A Pio Rajna, da Quaderno di quattro anni, 1977) Pio Rajna Pio Rajna (Sondrio, 8 luglio 1847 – Firenze, 25 novembre 1930) è stato un filologo e critico letterario italiano. Indice 1 Biografia 2 Omaggi 3 Onorificenze 4 Opere principali 4.1 Studi 4.2 Curatele 5 Note 6 Bibliografia 7 Altri progetti 8 Collegamenti esterni Biografia Pio Rajna Nacque da Eugenio Paolo Rajna e Costanza Simonetta....

明朝关西八卫 赤斤蒙古卫,明朝关西八卫之一,简称赤斤卫,又作赤金卫。 明朝 明朝永乐二年(1404年)元朝丞相苦术之子塔力尼投降明朝,以其所部在赤斤站设置赤斤蒙古千户所,在今甘肃省玉门市西北赤金堡。永乐八年(1410年)升为赤斤卫,正德年间被吐鲁番汗国所破,当地人内徙肃州的南山,赤斤城空。 清朝 清圣祖康熙五十七年(1718年),恢复赤金卫,清世宗雍正...

Triple woodhenge in Ohio, US Moorehead CircleLocation within Ohio todayLocationLebanon, Ohio, Warren County, Ohio, USARegionWarren County, OhioCoordinates39°24′27.22″N 84°5′16.8″W / 39.4075611°N 84.088000°W / 39.4075611; -84.088000HistoryCulturesOhio Hopewell cultureSite notesExcavation dates2009ArchaeologistsRobert RiordanArchitectureArchitectural stylestimber circle, Moorehead Circle was a triple woodhenge constructed about two millen...

Ej att förväxla med den finländske skogsforskaren och rektorn Erik Lönnroth. Erik Lönnroth Erik Lönnroth utövade både genom sin rent vetenskapliga gärning och genom sin verksamhet som universitets- och forskningspolitiker ett stort inflytande på svensk kulturpolitik under mer än ett halvt sekel. Foto från 1962.Född1 augusti 1910[1]Vasa församling[2]Död10 mars 2002[3] (91 år)Johannebergs församling[3]BegravdÖstra kyrkogården, Göteborg[3]kartorMedborgare ...

У этого термина существуют и другие значения, см. Поречье. ДеревняПоречье Казанская церковь в Поречье 55°37′12″ с. ш. 36°30′32″ в. д.HGЯO Страна Россия Субъект Федерации Московская область Муниципальный район Рузский Сельское поселение Колюбакинское История и г�...

Person who offers loans at extremely high interest rates For other uses, see Loan shark (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Loan shark – news · newspape...

Spanish conquistador (1485–1547) For the Bolivian Olympic weightlifter, see Hernán Cortez (weightlifter). In this Spanish name, the first or paternal surname is Cortés de Monroy and the second or maternal family name is Pizarro Altamirano. Hernán Cortés18th-century portrait of Cortés based on the one sent by the conqueror to Paolo Giovio, which has served as a model for many of his representations since the 16th century1st Governor of New SpainIn office13 August 1521 �...

Political term in Imperial Japan Mainland JapanNative name: 内地Passports for passengers between Mainland Japan and Okinawa during 1952–1972.GeographyLocationJapanDemographicsEthnic groupsJapanese peopleAinu peopleRyukyuan people Mainland Japan (内地, naichi, lit. inner lands) is a term used to distinguish Japan's core land area from its outlying territories. It is most commonly used to distinguish the country's four largest islands (Hokkaidō, Honshū, Kyūshū and Shikoku) from smalle...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wilhelmshaven Imperial Shipyard – news · newspapers · books · scholar · JSTOR (November 2007) (Learn how and when to remove this message) Kaiserliche Werft WilhelmshavenIndustryShipbuildingFounded1871Defunct1918FateClosed after World War ISuccessorKriegsmarinew...

Fictional female collie dog This article is about the fictional collie dog. For other uses, see Lassie (disambiguation). Fictional character LassieTommy Rettig with Lassie Junior, son of Pal, the first Lassie, in the Lassie television seriesFirst appearanceLassie Come-HomeCreated byEric KnightPortrayed byPalIn-universe informationSpeciesDog (Rough Collie)GenderFemale Lassie is a fictional female Rough Collie dog and is featured in a 1938 short story by Eric Knight that was later expanded to a...

FC 08 HomburgCalcio Segni distintiviUniformi di gara Casa Trasferta Colori sociali Verde, bianco Dati societariCittàHomburg Nazione Germania ConfederazioneUEFA Federazione DFB Fondazione1908 Presidente Herbert Eder StadioWaldstadion(22,500 posti) Sito webwww.fc08homburg.de/ PalmarèsSi invita a seguire il modello di voce L'Fußball-Club 08 Homburg/Saar e.V. è una società calcistica tedesca di Homburg, città del Saarland. I colori sociali sono il verde e il bianco. Nella stagione 2023...

Group of lymphoproliferative disorders Medical conditionCastleman diseasesOther namesGiant lymph node hyperplasia, lymphoid hamartoma, angiofollicular lymph node hyperplasiaMicrograph of Castleman disease showing hyaline vascular features including atrophic germinal center, expanded mantle zone, and a radially penetrating sclerotic blood vessel (lollipop sign). H&E stain.SpecialtyImmunology, angiology Symptomsfever, unintended weight loss, fatigue, night sweats, nausea, enlarged live...