The Unsustainable Lifestyle

The Unsustainable Lifestyle
Studio album by
Beauty Pill
ReleasedMarch 15, 2004
RecordedApril 2002 – July 2003
GenreIndie rock
LabelDischord Records[1]
Beauty Pill chronology
You Are Right To Be Afraid
(2003) 		The Unsustainable Lifestyle
(2004) 		Beauty Pill Describes Things As They Are
(2015)
Professional ratings
Review scores
SourceRating
AllMusic[2]
Pitchfork5.7/10[3]

The Unsustainable Lifestyle is the first full-length CD by indie rock band Beauty Pill.[4] It was released in 2004 on Dischord Records.

Track listing

  1. "Goodnight for Real" – 4:48
  2. "Lifeguard in Wintertime" – 4:32
  3. "The Mule on the Plane" – 4:38
  4. "Prison Song" – 3:10
  5. "The Western Prayer" – 3:40
  6. "Won't You Be Mine" – 3:26
  7. "Such Large Portions!" – 4:53
  8. "Nancy Medley, Girl Genius, Age 15" – 5:01
  9. "Quote Devout Unquote" – 5:00
  10. "Drive Down the Cost" – 4:15
  11. "I'm Just Gonna Close My Eyes for a Second" – 3:33
  12. "Terrible Things" – 2:48

References

  1. ^ Washington, Dischord Records 3819 Beecher St NW; U.s.a. 703.351.7507, Dc 20007-1802. "Beauty Pill - The Unsustainable Lifestyle (139)". Dischord Records.{{cite web}}: CS1 maint: numeric names: authors list (link)
  2. ^ "The Unsustainable Lifestyle - Beauty Pill | Songs, Reviews, Credits". AllMusic.
  3. ^ "Beauty Pill: The Unsustainable Lifestyle". Pitchfork.
  4. ^ "Beauty Pill The Unsustainable Lifestyle". exclaim.ca.


Stub icon

This 2000s indie rock album–related article is a stub. You can help Wikipedia by expanding it.

Read other articles:

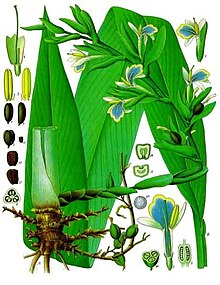
Elettaria

Elettaria Elettaria cardamomum Klasifikasi ilmiah Kerajaan: Plantae Upakerajaan: Trachaeophyta Divisi: Magnoliophyta Kelas: Liliopsida Subkelas: Commelinidae Ordo: Zingiberales Famili: Zingiberaceae Subfamili: Alpinioideae Tribus: Alpinieae Genus: ElettariaMaton, 1811 Spesies[1] Elettaria cardamomum (L.) Maton Elettaria ensal (Gaertn.) Abeyw. Sinonim[1] Cardamomum Noronha Matonia Stephenson & J.M.Churchill Elettaria adalah genus tumbuhan berbunga dalam keluarga Zingiberac...

 

 

John Fendall

John Fendall Jr. Gubernur Jenderal Hindia Belanda ke-37Masa jabatan11 Maret 1816 – 15 Agustus 1816Penguasa monarkiGeorge III PendahuluStamford RafflesPenggantiGodert van der Capellen Informasi pribadiLahir9 Oktober 1762St. Andrew, Holburn, London, InggrisMeninggal10 November 1825 (umur 63)Kalkuta, Pemerintahan BEIC atas IndiaSunting kotak info • L • B John Fendall, Jr. (9 Oktober 1762 – 10 November 1825) adalah seorang pejabat Inggris yang diserahi tug...

 

 

sensus Amerika Serikat

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari United States Census di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan pen...

العلاقات الكوستاريكية المالطية

العلاقات الكوستاريكية المالطية كوستاريكا مالطا   كوستاريكا   مالطا تعديل مصدري - تعديل   العلاقات الكوستاريكية المالطية هي العلاقات الثنائية التي تجمع بين كوستاريكا ومالطا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: و�...

 

 

Australia national baseball team at the Summer Olympics

See also: Australia national baseball team and Baseball at the Summer Olympics The Australia national baseball team was the third nation, after the United States and Sweden,[1] to participate in baseball at the Summer Olympics, making their first appearance at the 1956 Games in Melbourne, and again as part of its demonstration at the 1988 Games in Seoul. Since baseball was first included as a medal sport at the 1992 Games in Barcelona,[2] Australia has participated in three of...

 

 

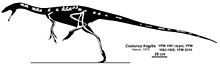
Coelurus

Coelurus Periode Jura Akhir, 155–152 jtyl PreЄ Є O S D C P T J K Pg N ↓ Restorasi kerangka, menunjukkan sisa-sisa yang diketahuiTaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSaurischiaFamiliCoeluridaeGenusCoelurus Tata namaSinonim takson Coelurus agilis Marsh, 1884 Elaphrosaurus agilis (Marsh, 1884) Russell, Beland & McIntosh, 1980 lbs Coelurus (/sɪˈljʊərəs/ si-LURE-əs, ekor berongga, dari kata bahasa Yunani κοῖλος, koilos = berongga + οὐρά, oura...

Pantai Teluk Awur

Pantai Teluk Awur Lokasi di Indonesia Informasi Lokasi Jepara. Negara  indonesia Koordinat 6°07′36″S 110°24′00″E / 6.1268°S 110.400°E / -6.1268; 110.400Koordinat: 6°07′36″S 110°24′00″E / 6.1268°S 110.400°E / -6.1268; 110.400 Pemilik Pengelola Pemdes Telukawur Dibuat oleh Pemkab Jepara Jenis objek wisata Wisata pantai Fasilitas  • Pantai  • Taman • Banana Boat • Kamar Bilas • Dermag...

 

 

Hell Gap complex

The Hell Gap complex is a Plano culture from 10,060 to 9,600 before present.[nb 1] It is named after the Hell Gap archaeological site, in Goshen County, Wyoming. Other Hell Gap complex sites In addition to the Hell Gap archaeological site, other Wyoming archaeological sites include the Sister's Hill site in northeastern Wyoming and a bison kill site near Casper, Wyoming.[1] Jones-Miller Bison Kill Site is the only Hell Gap complex site in Colorado.[2] Hell Gap point Th...

 

 

Dirección General de Formación Profesional

Dirección General de Formación Profesional Logotipo de la Dirección General de Formación Profesional Sede del MinisterioLocalizaciónPaís EspañaInformación generalSigla DGFPJurisdicción EspañaTipo Dirección GeneralSede Calle de Alcalá, 3428014 MadridOrganizaciónDepende de Secretaría de Estado de Educación y Formación ProfesionalEntidad superior Ministerio de Educación y Formación ProfesionalPresupuesto 189,6 millones de € (2019)HistoriaFundación 29 de febrero de ...

1908 Tennessee gubernatorial election

Election for the governorship of the U.S. state of Tennessee For related races, see 1908 United States gubernatorial elections. 1908 Tennessee gubernatorial election ← 1906 November 3, 1908 1910 →   Nominee Malcolm R. Patterson G. N. Tillman Party Democratic Republican Popular vote 133,176 113,269 Percentage 53.73% 45.70% Governor before election Malcolm R. Patterson Democratic Elected Governor Malcolm R. Patterson Democratic Elections in Tennessee Federal gove...

 

 

Crossover dribble

Basketball technique This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Crossover dribble – news · newspapers · books · scholar · JSTOR (July 2007) (Learn how and when to remove this message) Cat Barber does a crossover dribble on Nigel Williams-Goss at the 2013 McDonald's All-American Boys Game Allen Iverson w...

 

 

Joseph Fiennes

Joseph Fiennes Joseph Alberic Fiennes (lahir 27 Mei 1970) merupakan seorang aktor berkebangsaan Inggris yang memenangkan nominasi Screen Actors Guild Award. Dia dilahirkan di Salisbury, Inggris. Dia berkarier di dunia film sejak tahun 1993. Filmografi Stealing Beauty (1996) Shakespeare in Love (1998) Elizabeth (1998) Martha, Meet Frank, Daniel and Laurence (1998) Forever Mine (1999) Enemy at the Gates (2001) Dust (2001) Leo (2002) Killing Me Softly (2003) Sinbad: Legend of the Seven Seas (200...

Roman Catholic Diocese of Teruel and Albarracín

Roman Catholic diocese in Spain Diocese of Teruel and AlbarracínDioecesis Terulensis et AlbarracinensisDiócesis de Teruel y AlbarracínTeruel CathedralLocationCountry SpainEcclesiastical provinceZaragozaMetropolitanZaragozaStatisticsArea11,867 km2 (4,582 sq mi)Population- Total- Catholics(as of 2010)93,60089,750 (95.9%)InformationDenominationCatholicSui iuris churchLatin ChurchRiteRoman RiteEstablished31 July 1577 (As Diocese of Teruel)7 September 1851 (As...

 

 

苏密特·雷迪

此生者传记条目需要补充更多可供查證的来源。 (2018年7月3日)请协助補充可靠来源，无法查证的在世人物内容将被立即移除。 苏密特·雷迪Buss Sumeeth Reddy基本資料代表國家/地區 印度出生 (1991-09-26) 1991年9月26日（32歲）主項：男子雙打職業戰績9勝–8負（男單）93勝–81負（男雙）6勝–6負（混雙）最高世界排名第26位（男雙-马奴·阿特里）（2015年3月12日 [1]）現時世界...

 

 

浪花礁

此條目之中立性有争议。其內容、語調可能帶有明顯的個人觀點或地方色彩。 (2012年4月29日)加上此模板的編輯者需在討論頁說明此文中立性有爭議的原因，以便讓各編輯者討論和改善。在編輯之前請務必察看讨论页。 浪花礁主權争议岛屿浪花礁卫星照片地理浪花礁 浪花礁的位置位置南中国海坐标16°3′N 112°33′E / 16.050°N 112.550°E / 16.050; 112.550群岛西沙群岛...

Maidstone West railway station

Railway station in Kent, England Maidstone WestGeneral informationLocationMaidstone, MaidstoneEnglandGrid referenceTQ755553Managed bySoutheasternPlatforms2Other informationStation codeMDWClassificationDfT category EKey dates25 September 1844Opened (Terminus)18 June 1856Through station openedPassengers2018/19 0.922 million Interchange  0.119 million2019/20 0.905 million Interchange  0.120 million2020/21 0.210 million Interchange  29,2892021/22 0.549 million I...

 

 

Blake Stephenson

British politician Blake StephensonMPOfficial portrait, 2024Member of Parliamentfor Mid BedfordshireIncumbentAssumed office 4 July 2024Preceded byAlistair StrathernMajority1,321 (3.3%) Personal detailsPolitical partyConservative Blake Stephenson is a British Conservative Party politician who has been Member of Parliament for Mid Bedfordshire since 2024.[1][2] Stephenson is a Central Bedfordshire local councillor representing the villages of Gravenhurst and Shillington. He ...

 

 

Long Island

Long Island Kings, Queens, Nassau và Suffolk thuộc Long Island với ranh giới không hoàn toàn chính xácĐịa lýVị tríĐại Tây DươngTọa độ40°48′B 73°18′T / 40,8°B 73,3°T / 40.8; -73.3Diện tích1.401 dặm vuông Anh (3.630 km2)Rộng23 dặm (37 km)Độ cao tương đối lớn nhất401 foot (122 m)Đỉnh cao nhấtJayne's HillHành chínhHoa KỳĐịa phương New YorkDân số7.647.286 (tính đến 2019)M�...

Hiệp hội bóng đá Đức

Hiệp hội bóng đá ĐứcUEFAThành lập28 tháng 1 năm 1900; 124 năm trước (1900-01-28)Trụ sởFrankfurt am MainGia nhập FIFA1904Gia nhập UEFA1954Chủ tịchFritz KellerWebsitedfb.de Hiệp hội bóng đá Đức (tiếng Đức: Deutscher Fußball-Bund [ˈdɔʏ̯t͡ʃɐ ˈfuːsbalbʊnt]; DFB [deːʔɛfˈbeː]) là cơ quan quản lý bóng đá ở Đức. Đây chính là thành viên sáng lập của cả FIFA và UEFA, DFB có thẩm quyền đối v...

 

 

Knot theory

Study of mathematical knots Examples of different knots including the trivial knot (top left) and the trefoil knot (below it) A knot diagram of the trefoil knot, the simplest non-trivial knot In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or unknot). In mathematical language, a kno...