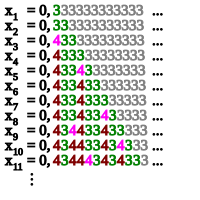
Specker sequence
|
Read other articles:

Untuk daftar, lihat Daftar ras kucing Seekor kucing ras Chinchilla Longhair dan Scottish Fold. Ras kucing adalah sekelompok kucing domestik yang memiliki karakteristik yang sangat mirip dan telah diterima oleh beberapa Organisasi Pendaftaran Kucing. Lihat pula Daftar ras kucing lbs Kucing domestikFelinologi Anak kucing Anatomi kucing Genetika kucing Indera kucing Kucing bermata ganjil Kucing kerdil Kucing polidaktil Kucing tupai Mutasi genetik Genetika bulu Kucing belang tiga Kucing biru Kuci...

Untuk teks Alkitabiah Bahasa Latin Kuno, lihat Vetus Latina. PemberitahuanTemplat ini mendeteksi bahwa artikel bahasa ini masih belum dinilai kualitasnya oleh ProyekWiki Bahasa dan ProyekWiki terkait dengan subjek. Terjadi [[false positive]]? Silakan laporkan kesalahan ini. 06.14, Sabtu, 30 Maret, 2024 (UTC) • hapus singgahan Sebanyak 1.305 artikel belum dinilai Artikel ini belum dinilai oleh ProyekWiki Bahasa Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Kol...

Annual LGBT event in Calgary, Alberta Calgary PrideThe official logo of Calgary PrideTypepride festivalLegal statusactivePurposeTo help see a city free from discrimination against gender identity, expression, and sexual orientation.HeadquartersCalgaryRegion served CalgaryWebsiteCalgary Pride Calgary Pride is an LGBT pride festival, held annually in Calgary, Alberta, Canada. The event is organized by Pride Calgary, a non-profit organization, and is currently held in the final week of August, w...

GertrudolfPenemuanDitemukan olehS. F. HönigSitus penemuanPalomarTanggal penemuan29 Agustus 2002PenamaanPenamaan MPC78433Penamaan alternatif2002 QF56Ciri-ciri orbitEpos 14 Mei 2008Aphelion2.7076494Perihelion2.5585480Eksentrisitas0.0283129Periode orbit1560.6271120Anomali rata-rata266.08706Inklinasi2.65829Bujur node menaik54.73053Argumen perihelion134.86183Ciri-ciri fisikMagnitudo mutlak (H)16.1 78433 Gertrudolf (2002 QF56) adalah sebuah asteroid yang terletak di s...

Noah Gray-CabeyNoah Gray-Cabey April 2009LahirNoah Gray-CabeyTahun aktif2002—sekarang Noah Gray-Cabey (lahir 16 November 1995) adalah aktor dan pianis asal Amerika Serikat. Dia berperan sebagai Franklin Aloysius Mumford dalam sitkom ABC My Wife and Kids dan Micah Sanders dalam drama fiksi sains milik NBC, Heroes. Filmografi Tahun Judul Sebagai Catatan 2002 My Wife and Kids Franklin Mumford 2002-2005 2003 Ripley's Believe It or Not 1 episode 2004 CSI: Miami Stevie Valdez Episode: Pro P...

Lancia Beta TreviDescrizione generaleCostruttore Lancia Tipo principaleBerlina 3 volumi Produzionedal 1980 al 1984 Sostituisce laLancia Beta Sostituita daLancia Prisma Esemplari prodotti40.628[senza fonte] Altre caratteristicheDimensioni e massaLunghezza4320 mm Larghezza1710 mm Altezza1400 mm Massa1165 kg AltroAssemblaggioChivasso (TO) La Lancia Beta Trevi è un modello di autovettura di categoria medio-superiore, prodotto dalla casa torinese Lancia ...

Canadian football player (born 1988) Arnaud Gascon-NadonNo. 95 Edmonton EskimosBorn: (1988-07-10) July 10, 1988 (age 35)Montreal, QuebecCareer informationStatusActiveCFL statusNationalPosition(s)DLHeight6 ft 3 in (191 cm)Weight250 lb (110 kg)CollegeRiceUniversityLavalCFL draft2012, Round: 3, Pick: 17Drafted byHamilton Tiger-CatsCareer historyAs player2013–2015Hamilton Tiger-Cats2016–2017Ottawa Redblacks2018–2019Edmonto...

South African military officer BrigadierPieter de WaalCB CBEColonel Pieter de WaalBorn(1899-12-31)December 31, 1899[1]Zeerust, South African RepublicDiedJune 1977Wynberg, Cape Town, Cape Province, South Africa (now Western Cape)AllegianceSouth AfricaService/branchSouth African NavyRankBrigadierService number179910VAwards Brigadier Pieter de Waal CB CBE (31 December 1899, Zeerust – June 1977, Wynberg)[2] was a South African military commander. He joined t...

Tennis tournament This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: 2012 BNP Paribas Open – Men's singles – news · newspapers · books · scholar · JSTOR (March 2012) (Learn how and when to remove this message) Men's singles2012 BNP Paribas OpenFinalChampion Roger FedererRunner-up John IsnerScore7–6(9–7), 6–3DetailsDraw96Seeds32Events Singles men wo...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

The RooftopPosterSutradaraJay ChouProduserHuang ZhimingWill LiuDitulis olehJay ChouPemeranJay ChouEric TsangXu FanLi Xin'aiAlan KoWang XueqiPenata musikJay ChouHuang YuxunSinematograferLee Ping-pinPerusahaanproduksiChuang Yi Motion PicturesEvergrande EntertainmentEdko FilmsBeijing Talent International MediaDistributorBuena Vista DistributionEdko FilmsTanggal rilis 11 Juli 2013 (2013-07-11) (Taiwan dan Tiongkok) 19 Juli 2013 (2013-07-19) (Amerika Utara) 01 Agustus 2013&...

Commonly known as IBSA, a three-country alignment India, Brazil, and South Africa Pretoria (South Africa) – Dilma Rousseff (President of Brazil), Jacob Zuma (President of South Africa), and Manmohan Singh (Prime Minister of India), pose for photo The IBSA Dialogue Forum (India, Brazil, South Africa) is an international tripartite grouping for promoting international cooperation among these countries. It represents three important poles for galvanizing South–South cooperation and greater u...

Stemma dell'Aquila Gonfalone ufficiale della città dell'Aquila Lo stemma dell'Aquila è costituito da uno scudo sannitico recante un'aquila di Svevia, nera su campo argento, sormontata da una corona e attorniata dalla scritta Immota manet e dal trigramma PHS. Nel gonfalone l'effigie è caricata su un drappo di velluto verde e accompagnata dagli stemmi dei quattro Quarti della città, ovvero San Marciano[1], Santa Maria, San Pietro e Santa Giusta[2]. Indice 1 Blasonatura 2 Sto...

National highway in India National Highway 505AMap of the National Highway in redRoute informationAuxiliary route of NH 5Length20 km (12 mi)Major junctionsNorth endPowariSouth endKalpa LocationCountryIndiaStatesHimachal Pradesh Highway system Roads in India Expressways National State Asian ← NH 5→ NH 505A National Highway 505A, commonly referred to as NH 505A is a national highway in India.[1][2] It is a spur road of National Highway 5.[3] ...

أدييوك الاسم الرسمي (بالقبردينية: Iэдийху) الإحداثيات 43°30′50″N 43°41′51″E / 43.513888888889°N 43.6975°E / 43.513888888889; 43.6975 تاريخ التأسيس 1988 تقسيم إداري البلد روسيا خصائص جغرافية ارتفاع 425 متر عدد السكان عدد السكان 1578 (2002)[1]1902 (2010)[2]2195 (2021)[3]...

Canadian law school University of Toronto Faculty of LawEstablished1949 (in current state)School typePublicDeanJutta BrunnéeLocationToronto, CanadaEnrollment815[1]Faculty125 [2]Websitewww.law.utoronto.ca The University of Toronto Faculty of Law (U of T Law, UToronto Law) is the law school of the University of Toronto. Maclean's has consistently assessed the Faculty as the highest ranked common law school in Canada and the highest ranked in terms of faculty journal citations.&...

American actor and comedian (1933–2019) Tim ConwayConway in 2007BornThomas Daniel ConwayDecember 15, 1933Chagrin Falls, Ohio, U.S.DiedMay 14, 2019(2019-05-14) (aged 85)Los Angeles, California, U.S.Resting placeWestwood Village Memorial Park, Westwood, California, U.S.Other namesTim Daniel ConwayThomas ConwayToma Daniel Conway1Alma materBowling Green State UniversityOccupationsActorcomedianwriterdirectorYears active1956–2016Spouses Mary Anne Dalton &#...
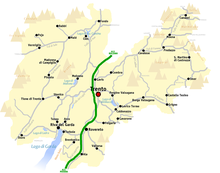
1998 incident involving a US Marine Corps aircraft and a cable car in Italy For the 1976 disaster, see 1976 Cavalese cable car crash. 1998 Cavalese cable car crashEA-6B BuNo 163045, the aircraft involved in the accident, photographed in 1997.Date3 February 1998; 26 years ago (1998-02-03)Time15:13 local time (CET)Locationnear Cavalese, Trentino, ItalyCauseControlled flight into obstacle, caused by pilot error.Casualties20 dead (1 cable car operator, 19 passengers)AccusedRicha...

Wolf 359 Data pengamatan Epos J2000 Ekuinoks J2000 Rasi bintang Leo Asensio rekta 10j 56m 28.99d[1] Deklinasi +07° 00′ 52.0″[1] Magnitudo tampak (V) 13.54[1] Ciri-ciri Kelas spektrum M6.5 Ve[1] Magnitudo semu (J) 7.1[1] Indeks warna U−B +1.165[2] Indeks warna B−V +2.034[2] Jenis variabel UV Ceti[3] AstrometriKecepatan radial (Rv)...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (octobre 2022). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? C...