Read other articles:

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

Bermuda Lacrosse AssociationSportLacrosseJurisdictionNationalFounded2002 (2002)AffiliationFederation of International LacrosseAffiliation date2006Official websitebermudalax.com The Bermuda Lacrosse Association is a group based on the island of Bermuda with the goal of promoting the sport of lacrosse on the island territory. The Bermuda Lacrosse Association is a member of the Federation of International Lacrosse and has participated at two previous World Championships, the 2006 World Lac...

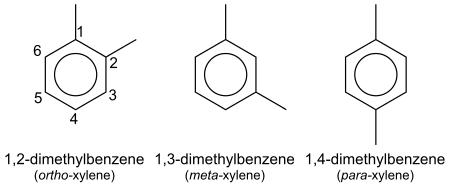
Organic compounds with the formula (CH3)2C6H4 The three xylene isomers: o-xylene, m-xylene, and p-xylene In organic chemistry, xylene or xylol (from Greek ξύλον (xylon) 'wood';[1][2] IUPAC name: dimethylbenzene) are any of three organic compounds with the formula (CH3)2C6H4. They are derived from the substitution of two hydrogen atoms with methyl groups in a benzene ring; which hydrogens are substituted determines which of three structural isomers results. I...

Wikipedia bahasa Turki Türkçe VikipediURLhttp://tr.wikipedia.org/TipeProyek ensiklopedia internetPerdagangan ?BukanRegistration (en)OpsionalLangueBahasa TurkiLisensiCreative Commons Atribusi-BerbagiSerupa 3.0 Tanpa Adaptasi dan Lisensi Dokumentasi Bebas GNU PemilikYayasan WikimediaService entry (en)5 Desember 2002 Wikipedia bahasa Turki adalah wikipedia edisi bahasa Turki. Pada April 2011, jumlah artikelnya mencapai 166.000 artikel. Beroperasi pada Desember 2002. Wikipedia ini merupak...

Supreme Court of the United States38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444EstablishedMarch 4, 1789; 235 years ago (1789-03-04)LocationWashington, D.C.Coordinates38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444Composition methodPresidential nomination with Senate confirmationAuthorized byConstitution of the United States, Art. III, § 1Judge term lengthl...

Big Bang Love, Juvenile ASutradaraTakashi MiikeProduserShiro SasakiTakeshi WatanabeDitulis olehMasa NakamuraSinematograferMasahito KanekoTanggal rilis26 Agustus 2006 (2006-08-26)Durasi85 menitNegaraJepangBahasaJepang Big Bang Love, Juvenile A (46億年の恋, 46-okunen no koi, lit. 4.6 billion year Love) adalah film Jepang tahun 2006 yang disutradarai oleh Takashi Miike. Pemeran Ryuhei Matsuda sebagai Jun Masanobu Ando sebagai Shiro Shunsuke Kubozuka Kiyohiko Shibukawa Jo Kanamori Kenich...

Pour les articles homonymes, voir Siège de Dantzig. Siège de Dantzig (1813) plan du siège en 1813 Informations générales Date 22 janvier 1813 au 2 janvier 1814 Lieu autour de Dantzig Issue Victoire russo-prussienne par reddition de la place Belligérants Empire français Confédération du Rhin Royaume de Bavière Royaume de Saxe Royaume de Prusse Empire russe Commandants • Jean Rapp • Matveï Platov •Alexandre de Wurtemberg • Friedrich von Löwis of Menar Forces en présence ~3...

Orang-orang Aztek sedang berbagi makanan. Kodeks Firenze, akhir abad ke-16. Hidangan Aztek adalah hidangan bekas Kekaisaran Aztek dan suku bangsa Nahua dari Lembah Meksiko sebelum kontak Eropa pada 1519. Hidangan paling menonjol adalah jagung, sebuah tumbuhan yang sangat berpengaruh di kalangan masyarakat Aztek yang memainkan peran utama dalam mitologi mereka. Referensi Bosland, Paul. (1999). Chiles: A Gift from a Fiery God. HortScience. 34(5): 810. Cambridge World History of Food (2000), 2 v...

Science and education district of Liverpool UK Human settlement in EnglandKnowledge Quarter, LiverpoolClockwise from top left: Liverpool Guild of Students; Victoria Gallery & Museum; Paddington Village; Liverpool School of Tropical Medicine; University of Liverpool; The Clatterbridge Cancer Centre; LJMU Redmonds Building and John Lennon Art and Design BuildingKnowledge Quarter, LiverpoolLocation within MerseysideOS grid referenceSJ3558790264Metropolitan boroughLiverpoolMetr...

Ancient Roman city near Pleven, Bulgaria Colonia Ulpia OescensiumSection of legionary fortress wall, OescusKnown also asOescusFounded during the reign ofTrajanFounded102Abandoned586Place in the Roman worldProvinceMesia superioreLimesDanubeStationed military units— Legions —Legio V Macedonica da Augusto a Traiano LocationCoordinates43°42′N 24°29′E / 43.700°N 24.483°E / 43.700; 24.483TownGigenCountyGulyantsi MunicipalityStatePleven ProvinceCountryBulgaria Loc...

У этого термина существуют и другие значения, см. Центр современного искусства. Зверевский центр современного искусства Дата основания 1992 Местонахождение Новорязанская улица Адрес 107066, Москва, Новорязанская улица, д. 29, стр. 4 Директор Алексей Сосна Сайт zverevcenter.ru  Меди�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2017) جيسيكا هولمز معلومات شخصية الميلاد 29 أغسطس 1973 (51 سنة)  أوتاوا  مواطنة كندا  الحياة العملية المدرسة الأم جامعة تورونتو متروبوليتان  المهنة ممثلة، &#...

Irish song published in 1808 Believe Me, If All Those Endearing Young Charms Instrumental, United States Air Force Band of the Rockies, Stellar Brass, 2007 Problems playing this file? See media help. Believe Me, If All Those Endearing Young Charms is a popular song written by the Irish poet Thomas Moore, setting new lyrics to a traditional Irish air that can be traced back into the 18th century.[1] He published it in 1808, naming the air as My Lodging is on the Cold Ground from lyrics...

This page is an archive of past discussions. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. Statistics portal listed for peer review I've listed the statistics portal for peer review here—G716 <T·C> 04:55, 22 May 2009 (UTC) Fisher consistency The introductory section of Fisher consistency is as opaquely and clumsily written as anything you'll see. I am still somewhat uncertain how best to rewrite...

Konflik bandit NigeriaBagian dari konflik penggembala-petani NigeriaBandit Nigeria pada 2021Tanggal2011–sekarang[2]LokasiDi seluruh barat laut NigeriaStatus BerlangsungPihak terlibat  Nigeria Kepolisian Nigeria Angkatan Bersenjata Nigeria Angkatan Darat Nigeria Angkatan Udara Nigeria Kelompok vigilante Kelompok Vigilante Nigeria Berbagai geng Milisi Hausa Milisi Fulani Dugaan keterlibatan Negara Islam – Provinsi Afrika Barat[1] Boko Haram Ansaru[1]Tokoh dan pe...

系列条目无政府主义 思想流派 黑人（英语：Black anarchism） 集體 共產 利己 认识论（英语：Epistemological anarchism） 存在（英语：Existentialist anarchism） 女性 綠色 個人 暴動（英语：Insurrectionary anarchism） 犹太（英语：Jewish anarchism） 互助 自然（英语：Anarcho-naturism） 和平 哲學（英语：Philosophical anarchism） 綱領（英语：Platformism） 后 後殖民（英语：Postcolonial anarchism） 後左翼（英...

此條目可参照英語維基百科相應條目来扩充。 (2019年9月16日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 此條目需要补充更多来源。 (2014年7月26日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能�...

Ocho Ríos Ciudad Vista de Ocho Ríos Glenn Standish Ocho RíosLocalización de Ocho Ríos en JamaicaCoordenadas 18°23′58″N 77°06′11″O / 18.399444, -77.103056Entidad Ciudad • País  JamaicaPoblación (2011)   • Total 16 671 hab.[editar datos en Wikidata] Vista de la ciudad Ocho Ríos es una ciudad situada en la costa norte de Jamaica, en la parroquia de Saint Ann. Según el censo de 2011, tiene una población de 16 671...

うつい けん宇津井 健 『日本の虎』（1954年、新東宝）スチル写真より本名 宇津井 健生年月日 (1931-10-24) 1931年10月24日没年月日 (2014-03-14) 2014年3月14日（82歳没）出生地 日本・東京府東京市深川区（現：東京都江東区）死没地 日本・愛知県名古屋市身長 173 cm血液型 A型職業 俳優ジャンル 映画・テレビドラマ・演劇活動期間 1952年 - 2014年配偶者 一般人との結婚を二度主な�...

System of numbers with non-finite quantities In mathematics, the Levi-Civita field, named after Tullio Levi-Civita,[1] is a non-Archimedean ordered field; i.e., a system of numbers containing infinite and infinitesimal quantities. It is usually denoted R {\displaystyle {\mathcal {R}}} . Each member a {\displaystyle a} can be constructed as a formal series of the form a = ∑ q ∈ Q a q ε q , {\displaystyle a=\sum _{q\in \mathbb {Q} }a_{q}\varepsilon ^{q},} where Q {\...