Puppe sequence
|
Read other articles:

Prasasti Kuburajo (juga disebut Prasasti Kuburajo I atau Prasasti Koeboer Radja) ditemukan di daerah Kuburajo 0°27′48″S 100°34′42″E / 0.463309°S 100.578461°E / -0.463309; 100.578461, Limo Kaum, Kabupaten Tanah Datar, Sumatera Barat pada tahun 1877 dan didaftarkan oleh N.J. Krom dalam Inventaris der Oudheden in de Padangsche Bovenlanden (OV 1912:41). Prasasti ini ditulis dalam bahasa Sanskerta, yang terdiri atas 16 baris tulisan. Prasasti ini merupakan salah...

Atribut-atribut Santo Homobonus (wafat 1197) meliputi sekantung uang Kantung uang adalah sebuah kantung uang (atau emas) yang dipakai untuk menyimpan dan membawa koin dan uang kertas dari/atau ke percetakan koin, bank, ATM, mesin jual otomatis, bisnis dan institusi lainnya.[1] Kantung-kantung uang biasanya dibawa dalam sebuah mobil bersenjata atau kereta uang dan lewat kereta pos pada masa lampau. Ini adalah jenis pengemasan mata uang. Referensi ^ Fallen money bag sparks Ohio cash gra...

Battle of Africa PointPart of the War of 1812The location of the Battle of Africa Point is in Crawford County, IllinoisDateApril 18, 1813Locationnear Fort LaMotte, Illinois TerritoryResult NoneBelligerents United States KickapooCommanders and leaders Captain Pierce Andrews UnknownStrength 12 unknownCasualties and losses 4 killed,2 badly wounded 5 killedvteOld Northwest 1811 Tippecanoe 1812 River Canard Fort Mackinac (1812) Brownstown Maguaga Fort Dearborn Detroit Credit Island Fort Harrison C...

For related races, see 2022 United States House of Representatives elections. 2022 United States House of Representatives elections in Nebraska ← 2020 November 8, 2022 2024 → All 3 Nebraska seats to the United States House of Representatives Majority party Minority party Party Republican Democratic Last election 3 0 Seats won 3 0 Seat change Popular vote 411,034 231,511 Percentage 62.71% 35.32% Swing 0.54% 0.69% Election results by distr...

For related races, see 2018 United States gubernatorial elections. 2018 Vermont gubernatorial election ← 2016 November 6, 2018 2020 → Turnout55.6% Nominee Phil Scott Christine Hallquist Party Republican Democratic Popular vote 151,261 110,335 Percentage 55.19% 40.25% County results Municipality resultsScott: 40–50% 50–60% 60–70% 70–...

Crystalline structure for solid elements For elements that are solid at standard temperature and pressure the first table gives the crystalline structure of the most thermodynamically stable form(s) in those conditions. Each element is shaded by a color representing its respective Bravais lattice, except that all orthorhombic lattices are grouped together. Standard temperature and pressure Crystal structure of elements in the periodic table at standard temperature and pressure[1] 1H&#...

2017 professional wrestling show This article is about the 2017 pro-wrestling event. For UK productions of War of the Worlds, see The War of the Worlds (disambiguation). War of the Worlds UKPromotional poster for the tourPromotionConsejo Mundial de Lucha LibreNew Japan Pro-WrestlingRevolution Pro WrestlingRing of HonorDateAugust 18, 19, and 20, 2017CityNight 1:London, England, U.K.Night 2:Liverpool, England, U.K.Night 3:Edinburgh, Scotland, U.K.Pay-per-view chronology ← PreviousBest in...

Questa voce sull'argomento calciatori liberiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Gizzie Dorbor Nazionalità Liberia Altezza 177 cm Calcio Ruolo Difensore Squadra Hapoel Kfar Kana CarrieraSquadre di club1 2003-2004 Karn United? (?)2005-2006 LISCR? (?)2007 Mighty Barrolle? (?)2008-2009 LISCR? (?)2009 Maccabi I. Bat Yam30 (1)2010-2011 Hapoel Herzliya53 (...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

2014 British documentary film 20,000 Days on EarthTheatrical release posterDirected byIain ForsythJane PollardWritten byIain ForsythJane PollardNick CaveProduced byDan BowenAlex DunnettJames WilsonCinematographyErik WilsonEdited byJonathan AmosMusic byNick CaveWarren EllisProductioncompaniesCorniche PicturesBritish Film InstituteFilm4 ProductionsPulse FilmsDistributed byPicturehouse Entertainment[1]Release dates 20 January 2014 (2014-01-20) (Sundance Film Festival) ...

India Template‑class India portalThis template is within the scope of WikiProject India, which aims to improve Wikipedia's coverage of India-related topics. If you would like to participate, please visit the project page.IndiaWikipedia:WikiProject IndiaTemplate:WikiProject IndiaIndia articlesTemplateThis template does not require a rating on Wikipedia's content assessment scale. Trains: Rapid transit Template‑class Trains Portal This template is within the scope of WikiProject Trains, an...

Public university in Essex, England This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (July 2023) (Learn how and when to remove this message) University of EssexCoat of armsMottoThought the harder, heart the keenerTypePublic research universityEstablished1964 – the first academic year1965 – received university ...

Untuk kementerian pemerintah Indonesia dengan nama serupa di Indonesia, lihat Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi Republik Indonesia. Kementerian Pendidikan dan Pengajaran Diraja Malaysia (Malay) Kementerian Pendidikan Federal Malaysia (Indonesian) 马来西亚皇家教育与教学部 (Mandarin) ராயல் மலேசியன் கல்வி மற்றும் கற்பித்தல் அமைச்சகம் (Tamil)Kementerian Pendidikan كمنتر�...

Amulo di Torinovescovo della Chiesa cattolica Incarichi ricopertiVescovo di Torino Nato? Consacrato vescovo898 Deceduto901, Torino Manuale Amulo di Torino (... – Torino, 901) è stato un vescovo italiano. Biografia Amulo fu vescovo di Torino dall'898 al 901. Compare a Pavia in un diploma dell'imperatore Guido, datato 11 luglio 892, nel quale è detto venerando presule della sacrosanta chiesa di Torino [1] Fu in guerra con la città di Torino, che all'epoca, non so...

Sycomune (dettagli) Sy – VedutaLa chiesa LocalizzazioneStato Francia RegioneGrand Est Dipartimento Ardenne ArrondissementVouziers CantoneVouziers AmministrazioneSindacoBruno Deswaene dal 2014 TerritorioCoordinate49°31′N 4°52′E49°31′N, 4°52′E (Sy) Superficie8,33 km² Abitanti51[1] (2014) Densità6,12 ab./km² Altre informazioniCod. postale08390 Fuso orarioUTC+1 Codice INSEE08434 CartografiaSy Modifica dati su Wikidata · Manuale Sy è un comun...

Questa voce sugli argomenti politici italiani e avvocati italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Franco De Lucia Sindaco di BariDurata mandato28 settembre 1981 –21 marzo 1990 PredecessoreLuigi Farace SuccessoreEnrico Dalfino Vicepresidente della Regione PugliaDurata mandato3 settembre 1993 –23 aprile 1995 PresidenteVito SavinoGiuseppe Martellotta Predece...
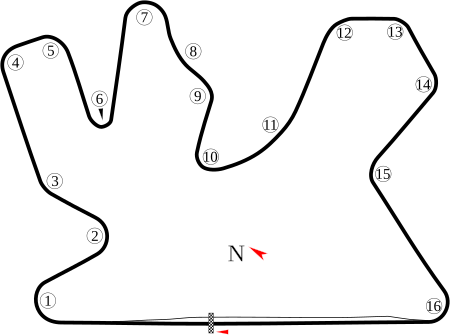
GP del Qatar 2019 924º GP della storia del Motomondiale1ª prova su 19 del 2019 Data 10 marzo 2019 Nome ufficiale VisitQatar Grand Prix Luogo Losail Percorso 5,380 km Risultati MotoGP 297º GP nella storia della classe Distanza 22 giri, totale 118,36 km Pole position Giro veloce Maverick Viñales Fabio Quartararo Yamaha in 1'53.546 Yamaha in 1'55.039 (nel giro 3 di 22) Podio 1. Andrea DoviziosoDucati 2. Marc MárquezHonda 3. Cal CrutchlowHonda Moto2 159º GP nella storia della classe ...

Tea blend flavoured with oil of bergamot Hot Earl Grey tea made in a teapot, and decanted into a teacup Earl Grey tea is a tea blend which has been flavoured with oil of bergamot. The rind's fragrant oil is added to black tea to give Earl Grey its unique taste.[1] However, many if not most Earl Greys use artificial bergamot flavour.[2] Traditionally, Earl Grey was made from black teas such as Chinese keemun, and therefore intended to be served without milk.[3] Sometime...

Yidis, Yidish ייִדיש / YídišHablado en Alemania Alemania Argentina AustraliaAustria AustriaBélgica BélgicaColombia ColombiaBielorrusia BielorrusiaBrasil BrasilCanadá CanadáChile Chile Estados UnidosHungría HungríaHonduras HondurasIsrael IsraelLituania LituaniaMéxico MéxicoMoldavia MoldaviaPaíses Bajos Países BajosPolonia PoloniaRumania RumaniaRusia RusiaSuecia SueciaSuiza Suiz...

Stephen F. Lynch Stephen Francis Lynch (lahir 31 Maret 1955) adalah seorang politikus Amerika Serikat yang menjabat sebagai anggota DPR mewakili Massachusetts sejak 2001. Ia berasal dari Partai Demokrat. Pranala luar Wikimedia Commons memiliki media mengenai Stephen Lynch (politician). Congressman Stephen Lynch official U.S. House website Stephen Lynch for Congress campaign website Stephen Lynch di Curlie (dari DMOZ) Biografi di Biographical Directory of the United States Congress Catatan sua...

![{\displaystyle \dots \to [Z,X_{n+1}]\to [Z,X_{n}]\to [Z,X_{n-1}]\to \dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9f4e3b3387b441c06342eda5bf5f7d15b6c54d4)











![{\displaystyle {\begin{aligned}\cdots &\to \pi _{n+1}(A)\to \pi _{n+1}(Y)\to \left[S^{0},\Omega ^{n}(Mi)\right]\to \pi _{n}(A)\to \pi _{n}(Y)\to \cdots \\\cdots &\to \pi _{1}(A)\to \pi _{1}(Y)\to \left[S^{0},Mi\right]\to \pi _{0}(A)\to \pi _{0}(Y)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d1f9aa939f83b75a1c677ae1d5e37542f8ff39)


![{\displaystyle [U,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d41ed98a535fa4b17d68d0d5e73f6a09c0cc666)

![{\displaystyle \left[S^{0},\Omega ^{n}(Mi)\right]=\left[S^{n},Mi\right]=\pi _{n}(Mi)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30202aa4fd8d4dcc76c00ea109b2dca1a8d8c8ba)







![{\displaystyle \pi _{n}(Mp)=\left[S^{n},Mp\right]\simeq \left[S^{n},F\right]=\pi _{n}(F).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d2bd8ca275864a069f5fa15ba9dadb39be22a62)


















