In mathematics, the projection-slice theorem, central slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:

• Take a two-dimensional function f(r), project (e.g. using the Radon transform) it onto a (one-dimensional) line, and do a Fourier transform of that projection.
• Take that same function, but do a two-dimensional Fourier transform first, and then slice it through its origin, which is parallel to the projection line.

In operator terms, if

• F₁ and F₂ are the 1- and 2-dimensional Fourier transform operators mentioned above,
• P₁ is the projection operator (which projects a 2-D function onto a 1-D line),
• S₁ is a slice operator (which extracts a 1-D central slice from a function),

then

${\displaystyle F_{1}P_{1}=S_{1}F_{2}.}$

This idea can be extended to higher dimensions.

This theorem is used, for example, in the analysis of medical CT scans where a "projection" is an x-ray image of an internal organ. The Fourier transforms of these images are seen to be slices through the Fourier transform of the 3-dimensional density of the internal organ, and these slices can be interpolated to build up a complete Fourier transform of that density. The inverse Fourier transform is then used to recover the 3-dimensional density of the object. This technique was first derived by Ronald N. Bracewell in 1956 for a radio-astronomy problem.^[1]

In N dimensions, the projection-slice theorem states that the Fourier transform of the projection of an N-dimensional function f(r) onto an m-dimensional linear submanifold is equal to an m-dimensional slice of the N-dimensional Fourier transform of that function consisting of an m-dimensional linear submanifold through the origin in the Fourier space which is parallel to the projection submanifold. In operator terms:

${\displaystyle F_{m}P_{m}=S_{m}F_{N}.\,}$

In addition to generalizing to N dimensions, the projection-slice theorem can be further generalized with an arbitrary change of basis.^[2] For convenience of notation, we consider the change of basis to be represented as B, an N-by-N invertible matrix operating on N-dimensional column vectors. Then the generalized Fourier-slice theorem can be stated as

${\displaystyle F_{m}P_{m}B=S_{m}{\frac {B^{-T}}{|B^{-T}|}}F_{N}}$

where ${\displaystyle B^{-T}=(B^{-1})^{T}}$ is the transpose of the inverse of the change of basis transform.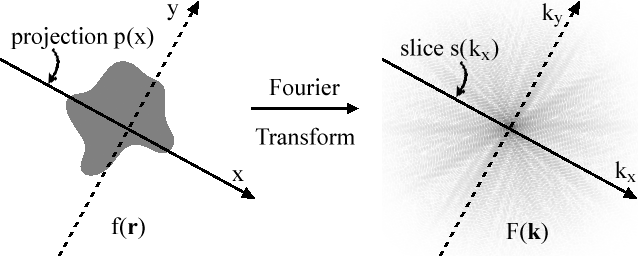

The projection-slice theorem is easily proven for the case of two dimensions. Without loss of generality, we can take the projection line to be the x-axis. There is no loss of generality because if we use a shifted and rotated line, the law still applies. Using a shifted line (in y) gives the same projection and therefore the same 1D Fourier transform results. The rotated function is the Fourier pair of the rotated Fourier transform, for which the theorem again holds.

If f(x, y) is a two-dimensional function, then the projection of f(x, y) onto the x axis is p(x) where

${\displaystyle p(x)=\int _{-\infty }^{\infty }f(x,y)\,dy.}$

The Fourier transform of ${\displaystyle f(x,y)}$ is

${\displaystyle F(k_{x},k_{y})=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi i(xk_{x}+yk_{y})}\,dxdy.}$

The slice is then ${\displaystyle s(k_{x})}$

${\displaystyle s(k_{x})=F(k_{x},0)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi ixk_{x}}\,dxdy}$

${\displaystyle =\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx}$

${\displaystyle =\int _{-\infty }^{\infty }p(x)\,e^{-2\pi ixk_{x}}dx}$

which is just the Fourier transform of p(x). The proof for higher dimensions is easily generalized from the above example.

If the two-dimensional function f(r) is circularly symmetric, it may be represented as f(r), where r = |r|. In this case the projection onto any projection line will be the Abel transform of f(r). The two-dimensional Fourier transform of f(r) will be a circularly symmetric function given by the zeroth-order Hankel transform of f(r), which will therefore also represent any slice through the origin. The projection-slice theorem then states that the Fourier transform of the projection equals the slice or

${\displaystyle F_{1}A_{1}=H,}$

where A₁ represents the Abel-transform operator, projecting a two-dimensional circularly symmetric function onto a one-dimensional line, F₁ represents the 1-D Fourier-transform operator, and H represents the zeroth-order Hankel-transform operator.

The projection-slice theorem is suitable for CT image reconstruction with parallel beam projections. It does not directly apply to fanbeam or conebeam CT. The theorem was extended to fan-beam and conebeam CT image reconstruction by Shuang-ren Zhao in 1995.^[3]

• Radon transform § Relationship with the Fourier transform

• Bracewell, Ronald N. (1990). "Numerical Transforms". Science. 248 (4956): 697–704. Bibcode:1990Sci...248..697B. doi:10.1126/science.248.4956.697. PMID 17812072. S2CID 5643835.
• Bracewell, Ronald N. (1956). "Strip Integration in Radio Astronomy". Aust. J. Phys. 9 (2): 198. Bibcode:1956AuJPh...9..198B. doi:10.1071/PH560198.
• Gaskill, Jack D. (2005). Linear Systems, Fourier Transforms, and Optics. John Wiley & Sons, New York. ISBN 978-0-471-29288-3.
• Ng, Ren (2005). "Fourier Slice Photography" (PDF). ACM Transactions on Graphics. 24 (3): 735–744. doi:10.1145/1073204.1073256.
• Zhao, Shuang-Ren; Halling, Horst (1995). "Reconstruction of Cone Beam Projections with Free Source Path by a Generalized Fourier Method". Proceedings of the 1995 International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine: 323–7.
• Garces, Daissy H.; Rhodes, William T.; Peña, Néstor (2011). "The Projection-Slice Theorem: A Compact Notation". Journal of the Optical Society of America A. 28 (5): 766–769. Bibcode:2011JOSAA..28..766G. doi:10.1364/JOSAA.28.000766. PMID 21532686.

• Fourier Slice Theorem (video). Part of the "Computed Tomography and the ASTRA Toolbox" course. University of Antwerp. September 10, 2015.