Parastatistics
|
Read other articles:

KalibawangKapanewonNegara IndonesiaProvinsiDaerah Istimewa YogyakartaKabupatenKulon ProgoPemerintahan • PanewuHeri Darmawan, A.P., M.M.Populasi • Total33,387 jiwa (2.009-BPS BAPPEDA diupdate 24/06/2.013) jiwaKode Kemendagri34.01.12 Kode BPS3401110 Luas5.296,37 km²Desa/kelurahan- Kalibawang (Jawa: ꦏꦭꦶꦧꦮꦁ, translit. Kalibawang) adalah sebuah kecamatan di Kabupaten Kulon Progo, Provinsi Daerah Istimewa Yogyakarta, Indonesia. Kalibawang merupakan...
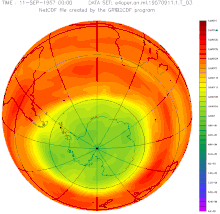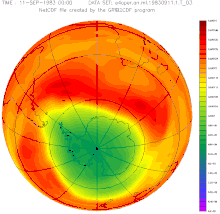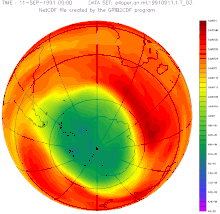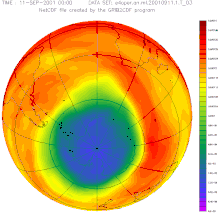
Lubang ozon di atas belahan bumi selatan antara tahun 1957–2001 Tanggal 16 September ditetapkan oleh Majelis Umum Persatuan Bangsa-Bangsa sebagai Hari Perlindungan Lapisan Ozon Sedunia. Ketetapan ini dibuat pada tanggal 19 Desember 1994 untuk memperingati tanggal ketika berbagai negara menandatangani Protokol Montreal tentang zat yang merusak lapisan ozon. Tema peringatan pada tahun 2013 adalah mengenai Kesehatan Atmosfer dan Masa Depan yang Kita Inginkan[1] Lihat pula Hari Aksi Ozo...

Jianghan 江汉区DistrikTaman ZhongshanJianghanLokasinya di HubeiKoordinat: 30°36′10″N 114°15′51″E / 30.6029°N 114.2642°E / 30.6029; 114.2642Koordinat: 30°36′10″N 114°15′51″E / 30.6029°N 114.2642°E / 30.6029; 114.2642[1]NegaraRepublik Rakyat TiongkokProvinsiHubeiKota subprovinsiWuhanLuas[2] • Total33,43 km2 (1,291 sq mi)Populasi (2010)[3] • Total683.492&...

Radio station in Nacogdoches, TexasKSFANacogdoches, TexasBroadcast areaLufkin/NacogdochesFrequency860 kHzBrandingNewsTalk 860 KSFAProgrammingFormatNews/talkAffiliationsFox News RadioCompass Media NetworksPremiere NetworksRadio AmericaWestwood OneStephen F. Austin State University (athletics)OwnershipOwnerTownsquare Media(Townsquare License, LLC)Sister stationsKAFX-FMKVLL-FMKYKSKTBQHistoryFirst air dateJune 2, 1947Call sign meaningStephen F. Austin or Stephen F. Austin State UniversityTechnica...

Pour les articles homonymes, voir Queen's. Queens Comté de Queens Sceau du comté. Drapeau du comté. La Unisphere, dans le Flushing Meadows-Corona Park, symbole de l'arrondissement. Administration Pays États-Unis État New York Chef-lieu Ville de New York Fondation 1683 Démographie Population 2 405 464 hab. (2020[1]) Densité 8 503 hab./km2 Géographie Coordonnées 40° 42′ 15″ nord, 73° 55′ 04″ ouest Superficie 28 290&...

American attorney and politician from Vermont George N. DaleU.S. Consul for Coaticook, Quebec, CanadaIn office1901–1902Preceded byJesse H. JohnsonSucceeded byFranklin D. HaleMember of the Vermont Senate from Essex CountyIn office1894–1896Preceded byFrederick A. TurnerSucceeded byJames H. BeattieIn office1866–1870Preceded byLewis H. TaborSucceeded byJohn W. HartshornLieutenant Governor of VermontIn office1870–1872GovernorJohn W. StewartPreceded byGeorge W. HendeeSucceeded byRussell S. ...

Fernando Alonso mengetes Renault R28 di Valencia Renault R28 merupakan sebuah mobil Formula Satu yang dirancang oleh tim Renault F1 untuk musim balap F1 2008. Mobil ini dirancang oleh Bob Bell, Pat Symonds, dan Denis Chevrier. Mobil ini berhasil memenangi balapan sebanyak dua kali yaitu di Singapura dan Jepang. Pembalap yang turun dengan mobil ini adalah Fernando Alonso dan Nelson Piquet Junior. Pranala luar Wikimedia Commons memiliki media mengenai Renault R28. Renault F1 R28 Tech Specs Diar...

William M. DaleyPotret resmi, 2011 Kepala Staf Gedung Putih ke-24Masa jabatan13 Januari 2011 – 27 Januari 2012PresidenBarack ObamaPendahuluRahm EmanuelPenggantiJack LewMenteri Perdagangan Amerika Serikat ke-32Masa jabatan30 Januari 1997 – 19 Juli 2000PresidenBill ClintonPendahuluMickey KantorPenggantiNorman Mineta Informasi pribadiLahirWilliam Michael Daley9 Agustus 1948 (umur 75)Chicago, Illinois, Amerika SerikatPartai politikPartai DemokratSuami/istriBernadette Ke...

Voce principale: Leonard Bernstein. Leonard Bernstein, ca. 1950s. Questa è una lista di composizioni del compositore americano Leonard Bernstein. Indice 1 Balletto 2 Opera 3 Musical 4 Musiche di scena ed altro teatro 5 Musica da film 6 Orchestra 7 Coro 8 Musica da camera 9 Musica vocale 10 Musica per pianoforte 11 Altra musica 12 Note 13 Bibliografia Balletto Fancy Free (in seguito ha fornito materiale per On the Town e West Side Story) (1944) Facsimile, Saggio coreografico per orchestra (1...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Reeling book – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message) Reeling First editionAuthorPauline KaelCountryUnited StatesLanguageEnglishGenreNon-fictionPublisherLittle BrownPublication date1976Pages49...

Pour les articles homonymes, voir Scream. Scream Chanson de Sergueï Lazarev au Concours Eurovision de la chanson 2019 Sortie 9 mars 2019 Durée 2:58 Format Téléchargement numérique Auteur-compositeur Sharon Vaughn; Dimitris Kontopoulos Chanson représentant la Russie au Concours Eurovision de la chanson 2019 I Won't Break(2018) Uno(2020)modifier Scream est une chanson de Sergey Lazarev qui représente la Russie au Concours Eurovision de la chanson 2019, à Tel Aviv en Israël. Elle ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أغسطس 2023) دورة الألعاب الأمريكية 1979 البلد الولايات المتحدة المدينة المضيفة سان خوان �...

The Heathen Woman's FriendThe women that publish the tidings are a great hostTypemonthlyOwner(s)Woman's Foreign Missionary Society of the Methodist Episcopal ChurchFounder(s)Lois Lee Parker and Clementina Rowe ButlerEditorHarriet Merrick WarrenFoundedThe Heathen Woman's Friend, vol. 1, no. 1 (May 1869)[1]LanguageEnglishCeased publicationvol. 27, no. 6 (December 1895)[1]Relaunchedcontinued as Woman's Missionary Friend, vol. 27, no. 7 (January 1896)-vol. 73, no. 7 (August 1940)&...

Mountainous region in northeastern Greenland Not to be confused with Queen Louise Island. Queen Louise LandNuna Dronning LouiseDronning Louise LandQueen Louise Land ONC map section.Highest pointPeakGefiontindeElevation2,364 m (7,756 ft)DimensionsLength185 km (115 mi) N/SWidth73 km (45 mi) E/WArea12,000 km2 (4,600 sq mi)GeographyQueen Louise LandLocation CountryGreenlandRange coordinates76°40′N 24°30′W / 76.667°N ...

1895–1896 war between the Ethiopia and Italy This article is about the war of 1895–1896. For the earlier, undeclared war between Italy and Ethiopia, see Italo-Ethiopian War of 1887–1889. For other wars between Italy and Ethiopia, see Italo-Ethiopian war (disambiguation). First Italo-Ethiopian WarPart of the Scramble for AfricaClockwise from top left: Menelik II at Adwa; The death of Major Toselli; Oreste Baratieri in Eritrea; Ras Mengesha on horseback; Illustration of Dabormida's last r...

Chinese brown sugar Peen tong at a supermarket in Haikou, Hainan, China Peen tong or pian tang (Chinese: 片糖; pinyin: piàntáng; Jyutping: pin3 tong4; Cantonese Yale: pintòng) and wong tong (Chinese: 黃糖; pinyin: huángtáng; Jyutping: wong4 tong4; Cantonese Yale: wòngtòng),[1] is a Chinese brown sugar and sugar candy that is used in various Chinese desserts and also consumed alone as a snack.[2][3][4] In China, it is s...

Memphis Open 2017Sport Tennis Data13 – 19 febbraio Edizione116ª CategoriaATP Tour 250 SuperficieCemento indoor Montepremi642 750$ LocalitàMemphis, Stati Uniti ImpiantoRacquet Club of Memphis CampioniSingolare Ryan Harrison Doppio Brian Baker / Nikola Mektić 2016 Il Memphis Open 2017 (anche conosciuto come Memphis Open Presented by ServiceMaster per motivi di sponsorizzazione e precedentemente noto come U.S. National Indoor Tennis Championships) è stato un torneo di tennis che si è...

MilazzoKomuneComune di MilazzoNegaraItaliaWilayahSisiliaProvinsiMessina (ME)FrazioniSantamarina, Bastione, Grazia, S.Pietro, S.Marco, S.Giovanni, FiumarellaPemerintahan • Wali kotaCarmelo Pino (Civic List)Luas • Total24,23 km2 (936 sq mi)Ketinggian1 m (3 ft)Populasi (2007) • Total32.650 • Kepadatan13/km2 (35/sq mi)DemonimMilesi/MilazzesiZona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos98...

Pour les articles homonymes, voir Allyson et Félix. Allyson Felix Allyson Felix à Rio en 2016 Informations Nom de naissance Allyson Michelle Felix Disciplines 100 m, 200 m, 400 m Période d'activité 2001-2022 Site officiel www.allysonfelix.com Nationalité Américaine Naissance 18 novembre 1985 (38 ans) Los Angeles (Californie) Taille 1,68 m (5′ 6″)[1] Masse 55 kg (121 lb)[1] Surnom Chicken Legs Entraîneur Bob Kersee Records • Record du monde du relais 4 ×...

Award2000 Mnet Music Video FestivalDateNovember 24, 2000 (2000-11-24)LocationLittle Angels Arts Center, Seoul, South KoreaHosted byCha Tae-hyun and Kim Hyun-jooMost awardsJo Sung-mo (2)Most nominationsH.O.T., Jo Sung-mo (3)WebsiteMnet Asian Music AwardsTelevision/radio coverageNetworkSouth Korea: MnetJapan: Mnet JapanRuntimearound 160 minutes ← 1999 · Mnet Asian Music Awards · 2001 → The 2000 Mnet Music Video Festival (MMF) was the second of t...

![{\displaystyle {\big [}a_{k},[a_{l}^{\dagger },a_{m}]_{\pm }{\big ]}_{-}=[a_{k},a_{l}^{\dagger }]_{\mp }a_{m}\pm a_{l}^{\dagger }[a_{k},a_{m}]_{\mp }\pm [a_{k},a_{m}]_{\mp }a_{l}^{\dagger }+a_{m}[a_{k},a_{l}^{\dagger }]_{\mp }=2\delta _{kl}a_{m},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed69f8b8cc5f733eb0e87adcf6426ff9bc3b3bb7)
![{\displaystyle {\big [}a_{k},[a_{l}^{\dagger },a_{m}^{\dagger }]_{\pm }{\big ]}_{-}=[a_{k},a_{l}^{\dagger }]_{\mp }a_{m}^{\dagger }\pm a_{l}^{\dagger }[a_{k},a_{m}^{\dagger }]_{\mp }\pm [a_{k},a_{m}^{\dagger }]_{\mp }a_{l}^{\dagger }+a_{m}^{\dagger }[a_{k},a_{l}^{\dagger }]_{\mp }=2\delta _{kl}a_{m}^{\dagger }\pm 2\delta _{km}a_{l}^{\dagger },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd6862c046d8cd9d3ef4408c97031cbd36a9cfa)
![{\displaystyle {\big [}a_{k},[a_{l},a_{m}]_{\pm }{\big ]}_{-}=[a_{k},a_{l}]_{\mp }a_{m}\pm a_{l}[a_{k},a_{m}]_{\mp }\pm [a_{k},a_{m}]_{\mp }a_{l}+a_{m}[a_{k},a_{l}]_{\mp }=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e01c6d035202752b808b95339683dc14f2a30fc)

![{\displaystyle [\phi ^{(i)}(x),\phi ^{(i)}(y)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96b3b1b66e72ec63d5b86b56b67816c31ee8160)




![{\displaystyle [\psi ^{(i)}(x),\psi ^{(j)}(y)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45cef605b79f8fcdf86d63798d4f096a1ed18ac)





![{\displaystyle {\mathcal {E}}(\pi ){\big [}\phi (x_{1})\cdots \phi (x_{n})|\Omega \rangle {\big ]}=\phi (x_{\pi ^{-1}(1)})\cdots \phi (x_{\pi ^{-1}(n)})|\Omega \rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bbce10a9840f658663e256cf3e100c160591f92)
![{\displaystyle {\mathcal {E}}(\pi ){\big [}\psi (x_{1})\cdots \psi (x_{n})|\Omega \rangle {\big ]}=\psi (x_{\pi ^{-1}(1)})\cdots \psi (x_{\pi ^{-1}(n)})|\Omega \rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c8ac30d497f0467d07906b7d0bec724c5132ffc)
