Ontology components
|
Read other articles:

لمعانٍ أخرى، طالع ليمستون (توضيح). ليمستون الإحداثيات 42°01′34″N 78°37′59″W / 42.0261°N 78.6331°W / 42.0261; -78.6331 [1] تاريخ التأسيس 7 ديسمبر 1877 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كاتاروغوس خصائص جغرافية المساحة 4.230049 كيل...

British cyclist (born 1976) For the American politician, see Chris Hoy (politician). SirChris HoyMBEHoy at the Homecoming Parade in Glasgow in 2012Personal informationFull nameChristopher Andrew HoyBorn (1976-03-23) 23 March 1976 (age 48)Edinburgh, ScotlandHeight1.85 m (6 ft 1 in)[1]Weight92 kg (203 lb; 14 st 7 lb)[1]Team informationDisciplineTrackRoleRiderAmateur teams1984–1986Scotia BMX1986–1991GT Factory BMX Team1992–1993Du...

Burial places of justices of the Supreme Court of the United States are located across 26 states and the District of Columbia. The state with the most U.S. Supreme Court justice burial sites is Virginia with 20 – 14 of which are at Arlington National Cemetery. Since it was established in 1789, 114 persons have served as a justice (associate justice or chief justice) on the Supreme Court; of these, 104 have died. The first death of a justice was that of James Wilson on August 2...

Championship banners, Lakers retired jerseys, and honored Minneapolis Lakers banner hanging in the rafters of Crypto.com Arena This page details the all-time statistics, records, and other achievements pertaining to the Los Angeles Lakers. The Los Angeles Lakers are an American professional basketball team currently playing in the National Basketball Association. Laker individual accomplishments NBA MVP Kareem Abdul-Jabbar – 1976, 1977, 1980 Magic Johnson – 1987, 1989, 1990 Shaquille O'Ne...

Miye Oni Miye Oni in azione con la maglia di Yale Nazionalità Regno Unito Nigeria Altezza 196 cm Peso 95 kg Pallacanestro Ruolo Guardia Squadra Osceola Magic Carriera Giovanili Viewpoint School2015-2016Suffield Academy2016-2019 Yale Bulldogs Squadre di club 2019-2022 Utah Jazz80 (145)2019-2020→ S.L.C. Stars23 (291)2022 N.O. Pelicans0 (0)2022-2023 London Lions2023- Osceola Magic Nazionale 2021- Nigeria Il simbolo → indica un trasferimento i...

MTV Video Music Award for Best R&BAwarded forMusic songsCountryUnited StatesPresented byMTVFirst awarded1993Currently held bySZA – Shirt (2023)Most awardsAlicia Keys, Beyoncé, En Vogue, Destiny's Child & The Weeknd (2)Most nominationsAlicia Keys (8)WebsiteVMA website The MTV Video Music Award for Best R&B was first awarded in 1993 under the name Best R&B Video, and it was given every year until 2006. The following year MTV revamped the VMAs and eliminated all the genre cat...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

No debe confundirse con Micronesia. Estados Federados de MicronesiaFederated States of Micronesia (inglés)Bandera Sello Lema: Peace, Unity, Liberty(inglés: «Paz, Unidad, Libertad») Himno: Patriots of Micronesia(inglés: «Patriotas de Micronesia») ¿Problemas al reproducir este archivo? Capital Palikir6°55′04″N 158°11′06″E / 6.9177777777778, 158.185 Ciudad más poblada Weno7°27′N 151°51′E / 7.450, 151.850Idiomas oficiales Inglés...

Diagnostic testing for SARS-CoV-2 virus infection Part of a series on theCOVID-19 pandemicScientifically accurate atomic model of the external structure of SARS-CoV-2. Each ball is an atom. COVID-19 (disease) SARS-CoV-2 (virus) Cases Deaths Timeline 2019 2020 January responses February responses March responses April responses May responses June responses July responses August responses September responses October responses November responses December responses 2021 January responses February...

Questa voce sull'argomento calciatori britannici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Jason LoweNazionalità Inghilterra Altezza183 cm Peso72 kg Calcio RuoloCentrocampista Squadra Port Vale CarrieraGiovanili 2003-2010 Blackburn Squadre di club1 2010-2011 Blackburn1 (0)2011→ Oldham Athletic7 (2)2011-2017 Blackburn172 (1)2017-2018 Birmingham City9 (0)2018-...

Many countries around the world maintain military units that are specifically trained to operate in a cyberwarfare environment. In several cases these units act also as the national computer emergency response team for civilian cybersecurity threats. Albania Military Cyber Security Unit (Një e Sigurisë Kibernetike)[1] Argentina Joint Cyber Defense Command of the Armed Forces Joint Staff (Comando Conjunto de Ciberdefensa del Estado Mayor Conjunto de las Fuerzas Armadas)[2] C...

Choi Seung-heeLahir24 November, 1911HongcheonMeninggal8 Agustus, 1969Korea UtaraKebangsaanKorea UtaraNama lainSai ShokiPekerjaanPenari, koreograferSuami/istriAn Mak Choi Seung-hee (1911-1969) adalah seorang penari, penyanyi, dan bintang film dari Korea.[1][2][3][4] Ia dianggap sebagai seorang entertainer pertama dari Korea dan Asia yang dikenal luas oleh dunia internasional pada abad ke-20. Ia merupakan pencipta jenis tari kreasi baru Korea yang dinamakan...

French actor You can help expand this article with text translated from the corresponding article in French. (November 2021) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unr...

Type of dance RenaissanceThe School of Athens (1509–1511) by Raphael Aspects Architecture Dance Fine arts Greek scholars Humanism Literature Magic Music Philosophy Science Technology Warfare Regions England France Germany Italy Poland Portugal Spain Scotland Northern Europe Low Countries History and study Age of Discovery Continuity thesis High Renaissance vte Renaissance dances belong to the broad group of historical dances, specifically those during the Renaissance period. During that per...

Arab physicist, mathematician and astronomer (c. 965 – c. 1040) Alhazen redirects here. For other uses, see Alhazen (disambiguation). AlhazenḤasan Ibn al-Haythamابن الهيثمBornc. 965 (0965) (c. 354 AH)[1]Basra, Buyid EmirateDiedc. 1040 (1041) (c. 430 AH)[1] (aged around 75)Cairo, Fatimid CaliphateKnown forBook of Optics, Doubts Concerning Ptolemy, Alhazen's problem, analysis,[2] Catoptrics,[3] horopter, Spherical aberratio...
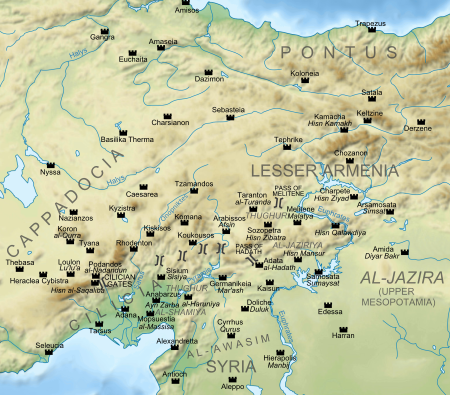
al-Thughur redirects here. For the frontiers of Islamic Spain, see Upper March, Central March, and Lower March. Muslim fortifications Thughur and Awasimاَلـثُّـغُـوْر وَالْـعَـوَاصِـمal-thughūr wa-l-ʿawāṣimCilicia, northern Syria and Upper Mesopotamia TypeFortified border zoneSite informationControlled byAbbasid Caliphate (750s–c. 930), Ikhshidids (c. 935–940s), Hamdanids (940s–962s), Mamluks of Egypt (14th century–1516)Site historyB...

American educational psychologist Charles Hubbard Judd (February 20, 1873 – July 18, 1946[1]) was an American educational psychologist who played an influential role in the formation of the discipline. Part of the larger scientific movement of this period, Judd pushed for the use of scientific methods to the understanding of education and, thus, wanted to limit the use of theory in the field. Judd was known for applying scientific methods to the study of educational issues. Born...

Humor through visualization rather than sound or words This image conveys a joke without the use of words. In comedy, a visual gag or sight gag is anything which conveys its humour visually, often without words being used at all. The gag may involve a physical impossibility or an unexpected occurrence.[1] The humor is caused by alternative interpretations of the goings-on.[2] Visual gags are used in magic, plays, and acting on television or movies. Types The most common type o...

Church in the United StatesEmmanuel ChurchEmmanuel Church in the City of BostonAddress15 Newbury Street Back Bay, Boston, MassachusettsCountryUnited StatesDenominationEpiscopalWebsiteWebsite of the ChurchHistoryStatusActiveFoundedJune 17, 1861 (1861-06-17)ConsecratedApril 24, 1862ArchitectureFunctional statusParish ChurchArchitect(s)Alexander Rice Esty, Francis Richmond AllenArchitectural typeNeo-GothicAdministrationDioceseMassachusettsClergyBishop(s)Alan M. GatesRectorPamela L...

British politician (1794–1878) For other people named Frederic Thesiger, see Frederic Thesiger (disambiguation). The Right HonourableThe Lord ChelmsfordPC, FRSLord High Chancellor of Great BritainIn office26 February 1858 – 11 June 1859MonarchVictoriaPrime MinisterThe Earl of DerbyPreceded byThe Lord CranworthSucceeded byThe Lord CampbellIn office6 July 1866 – 29 February 1868MonarchVictoriaPrime MinisterThe Earl of DerbyPreceded byThe Lord CranworthSucceeded byThe Lor...
