Only Folls Fall in Love |
Read other articles:

Thales RBE2 AESA. RBE2 (Radar à Balayage Electronique 2 plans) adalah very high performance radar multirole X band yang dikembangkan selama tahun 1990-an untuk pesawat tempur Dassault Rafale Prancis, yang menggabungkan fire control radar detection dan target tracking, yang merupakan hasil kolaborasi antara Thomson-CSF dan Dassault Electronics (sekarang Thales). RBE2 asli adalah passive electronically scanned array (PESA). Radar ini telah dikembangkan menjadi RBE2-AA, active electronically sc...

Wilayah Iceni Iceni atau Eceni adalah suku yang menghuni wilayah Britania antara abad ke-1 SM hingga abad ke-1 M. Iceni berbatasan dengan Corieltauvi di barat, Catuvellauni dan Trinovantes di selatan. Iceni tidak ditaklukan dalam invasi Romawi tahun 43, tetapi menjadi sekutu Romawi. Namun, Iceni bangkit melawan Romawi pada tahun 47 setelah Publius Ostorius Scapula mengancam melucuti mereka. Iceni dikalahkan oleh Ostorius dalam pertempuran yang sengit, tetapi masih dapat mempertahankan kemerde...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Bali PostPengemban Pengamal PancasilaTipeHarianFormatHarian koran pagiPemilikKelompok Media Bali PostPenerbitPT Bali PostDidirikan16 Agustus 1948 (umur 75)BahasaBahasa Ind...

The district duchy, also known as the district principality, was a type of the state under the patrimonial system, such as duchy or principality, formed in the feudal system, as a result of land partition between the members of a royal family.[1] It occurred in the Middle Ages and early modern period, notably in Europe, in states such as the Holy Roman Empire,[2] Duchy of Poland,[1][3] and Kievan Rus'.[4] Holy Roman Empire Bavaria Further information: D...

United States Navy admiral This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Clark H. Woodward – news · newspapers · books · scholar · JSTOR (June 2020) (Learn how and when to remove this template message) Clark H. WoodwardRADM Clark H. Woodward in 1919Birth nameClark Howell WoodwardNickname(s)WoodyBorn(1877-0...

Dominican baseball player (born 1977) Baseball player Fernando RodneyRodney with the Washington Nationals in 2019PitcherBorn: (1977-03-18) March 18, 1977 (age 47)Samaná, Dominican RepublicBatted: RightThrew: RightMLB debutMay 4, 2002, for the Detroit TigersLast MLB appearanceSeptember 28, 2019, for the Washington NationalsMLB statisticsWin–loss record48–71Earned run average3.80Strikeouts943Saves327 Teams Detroit Tigers (2002–2003, 2005–2009) Los Ang...

American actress (1902–1969) Thelma RitterRitter in All About Eve (1950)Born(1902-02-14)February 14, 1902New York City, U.S.DiedFebruary 5, 1969(1969-02-05) (aged 66)New York City, U.S.OccupationActressYears active1913–1968Spouse Joseph Moran (m. 1927)Children2 Thelma Ritter (February 14, 1902 – February 5, 1969) was an American character actress who was known for her strong New York City accent, diminutive size, and plain look favored wo...
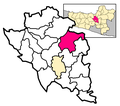
BringinKecamatanPeta lokasi Kecamatan BringinNegara IndonesiaProvinsiJawa TengahKabupatenSemarangPemerintahan • CamatKhabib Sholeh, S.pd,Populasi • Total- jiwaKode Kemendagri33.22.12 Kode BPS3322120 Luas61,89 km²Desa/kelurahan16 Bringin (Jawa: ꦧꦿꦶꦔꦶꦤ꧀, translit. Bringin) adalah sebuah kota kecamatan di Kabupaten Semarang, Jawa Tengah, Indonesia. Kecamatan ini berjarak sekitar 25 kilometer dari ibukota kabupaten Semarang ke arah tenggara. Ke...

Atsubetsu 厚別区Distrik kotaKantor Distrik Atsubetsu BenderaEmblemLokasi Distrik Atsubetsu di wilayah SapporoNegaraJepangWilayahHokkaidoPrefektur Hokkaido (Subprefektur Ishikari)KotaSapporoDidirikan6 November 1989Luas[1] • Total24,38 km2 (9,41 sq mi)Populasi (31 Oktober 2023) • Total124,075 • Kepadatan5.089,21/km2 (13,181,0/sq mi)Zona waktuUTC+09:00 (JST)Kode pos004-8612Alamat kantor distrik5-3-2 Atsubetsu Chūō-1-j...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

List of events ← 1890 1889 1888 1891 in the United States → 1892 1893 1894 Decades: 1870s 1880s 1890s 1900s 1910s See also: History of the United States (1865–1918) Timeline of United States history (1860–1899) List of years in the United States 1891 in the United States1891 in U.S. states States Alabama Arkansas California Colorado Connecticut Delaware Florida Georgia Idaho Illinois Indiana Iowa Kansas Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota Mississ...

Daong Cynoglossum Cynoglossum officinaleTaksonomiKerajaanPlantaeDivisiTracheophytaOrdoBoraginalesFamiliBoraginaceaeGenusCynoglossum Linnaeus, 1753 Cynoglossum atau bunga daong adalah genus tumbuhan berbunga kecil dalam keluarga Boraginaceae (keluarga borage). Cynoglossum officinale, daong biasa, berasal dari Asia, Afrika, dan Eropa. Tanaman ini telah diperkenalkan ke Amerika Utara, dan dianggap sebagai gulma yang mengganggu karena durinya menempel pada bulu domba dan hewan lain. Menelan tanam...

Isosceles triangle in which the duplicated side is in the golden ratio to the base side A golden triangle. The ratio a/b is the golden ratio φ. The vertex angle is θ = 36 ∘ {\displaystyle \theta =36^{\circ }} . Base angles are 72° each. Golden gnomon, having side lengths 1, 1, and ϕ {\displaystyle \phi } A golden triangle, also called a sublime triangle,[1] is an isosceles triangle in which the duplicated side is in the golden ratio φ {\displaystyle \varp...

English writer This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2021) (Learn how and when to remove this message) Ian HamiltonThe cover of Ian Hamilton's Collected PoemsBornRobert Ian Hamilton24 March 1938King's Lynn, Norfolk, EnglandDied27 December 2001 (2001-12-28) (aged 63)London, EnglandNationalityBritishEducationDarlington Grammar School...

Hypothetical aggregate building material, similar to concrete, formed from lunar regolith Laboratory-determined properties for lunarcrete[1][2] Compressive strength 39–75.7 N/mm2 (MPa) Young's modulus 21.4 kN/mm2 Density 2.6 g/cm3 Temperature coefficient 5.4 × 10−6 K−1 Lunarcrete, also known as mooncrete, an idea first proposed by Larry A. Beyer of the University of Pittsburgh in 1985, is a hypothetical construction aggregate, similar to concrete, formed from l...

Associazione Calcio MantovaStagione 2003-2004Sport calcio Squadra Mantova Allenatore Domenico Di Carlo Presidente Alberto Castagnaro Serie C21º posto nel girone A, promosso in Serie C1. Coppa Italia Serie Cottavi di finale Maggiori presenzeCampionato: Bellodi (33) Miglior marcatoreCampionato: Graziani (17 reti) StadioStadio Danilo Martelli 2002-2003 2004-2005 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Mantova nell...

Hungarian rabbi You can help expand this article with text translated from the corresponding article in Hebrew. (November 2015) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears ...