Nonconvex great rhombicuboctahedron

Nonconvex great rhombicuboctahedron
Type Uniform star polyhedron
Elements F = 26, E = 48
V = 24 (χ = 2)
Faces by sides 8{3}+(6+12){4}
Coxeter diagram
Wythoff symbol 3/2 4 | 2
3 4/3 | 2
Symmetry group Oh, [4,3], *432
Index references U17, C59, W85
Dual polyhedron Great deltoidal icositetrahedron
Vertex figure
4.4.4.3/2
Bowers acronym Querco
3D model of a nonconvex great rhombicuboctahedron

In geometry, the nonconvex great rhombicuboctahedron is a nonconvex uniform polyhedron, indexed as U17. It has 26 faces (8 triangles and 18 squares), 48 edges, and 24 vertices.[1] It is represented by the Schläfli symbol rr{4,3⁄2} and Coxeter-Dynkin diagram of . Its vertex figure is a crossed quadrilateral.

This model shares the name with the convex great rhombicuboctahedron, also called the truncated cuboctahedron.

An alternative name for this figure is quasirhombicuboctahedron. From that derives its Bowers acronym: querco.

Orthographic projections

Cartesian coordinates

Cartesian coordinates for the vertices of a nonconvex great rhombicuboctahedron centered at the origin with edge length 1 are all the permutations of

It shares the vertex arrangement with the convex truncated cube. It additionally shares its edge arrangement with the great cubicuboctahedron (having the triangular faces and 6 square faces in common), and with the great rhombihexahedron (having 12 square faces in common). It has the same vertex figure as the pseudo great rhombicuboctahedron, which is not a uniform polyhedron.


Truncated cube
Great rhombicuboctahedron
Great cubicuboctahedron
Great rhombihexahedron
Pseudo great rhombicuboctahedron

Great deltoidal icositetrahedron

Great deltoidal icositetrahedron
Type Star polyhedron
Face
Elements F = 24, E = 48
V = 26 (χ = 2)
Symmetry group Oh, [4,3], *432
Index references DU17
dual polyhedron Nonconvex great rhombicuboctahedron
3D model of a great deltoidal icositetrahedron

The great deltoidal icositetrahedron is the dual of the nonconvex great rhombicuboctahedron.

References

  1. ^ Maeder, Roman. "17: great rhombicuboctahedron". MathConsult.

Weisstein, Eric W. "Great Deltoidal Icositetrahedron". MathWorld.


Stub icon

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.

Read other articles:

Kantor India

Lihat pula: British Raj Bagian barat atau ujung taman dari gedung Jawatan Luar Negeri dan Persemakmuran pada 1866. Gedung tersebut kemudian diduduki oleh Jawatan Luar Negeri dan India, sementara Jawatan Dalam Negeri dan Kolonial menduduki ujung Whitehall. Kantor India (Inggris: India Officecode: en is deprecated ) adalah sebuah departemen pemerintahan Inggris yang dibuat pada tahun 1858 untuk mengurusi pemerintahan, melalui Viceroy dan para pejabat lainnya, dari provinsi-provinsi di India Bri...

 

Abu Bilal Mirdas

Abu Bilal MirdasMeninggal681Tawwaj/Darab, provinsi FarsZamanKekhalifahan UmayyahLawan politikUbaidillah bin ZiyadOrang tuaHudayr bin Amr (bapak)Udayya (ibu) Abu Bilal Mirdas ibn Udayya al-Tamimi (meninggal 681) adalah pemimpin Khawarij Basra yang quietisme selama tahun-tahun awal Kekhalifahan Umayyah. Dia adalah saudara laki-laki Urwa bin Udayya, salah satu penghasut gerakan Khawarij di Pertempuran Shiffin, yang diikuti oleh Abu Bilal sendiri. Setelah kekalahan kaum Khawarij dalam Pertempura...

 

Stasiun Minami-Kurume

Stasiun Minami-Kurume南久留米駅Stasiun Minami-Kurume pada 2006LokasiJepangKoordinat33°18′09″N 130°31′53″E / 33.30250°N 130.53139°E / 33.30250; 130.53139Koordinat: 33°18′09″N 130°31′53″E / 33.30250°N 130.53139°E / 33.30250; 130.53139Operator JR KyushuJalur■ Jalur Utama KyudaiLetak4.9 km dari KurumeJumlah peron1 peron pulauInformasi lainStatusMemiliki stafSitus webSitus web resmiSejarahDibuka24 Desember 1928 (19...

Orang Portugis

Bangsa Portugis (Portugis: Portugueses) merupakan bangsa asli Portugal yang secara genetik dan budaya dengan suku mediterania. Bangsa ini terutama menghuni di Portugal dan Brasil. Penduduk kecil Bangsa Portugis umumnya di Finlandia, Norwegia, Amerika Serikat, Austria, Argentina, Spanyol, Jerman, Denmark dan negara lainnya. Mereka menuturkan bahasa Portugis. Jumlah penduduk bangsa ini ialah lebih dari 15 juta jiwa umumnya menghuni Portugal. Di Indonesia, komunitas keturunan Portugis dalam juml...

 

Planes (film)

Planes: The MoviePoster rilis teatrikalSutradaraKlay Hall[1]ProduserTraci Balthazor-Flynn[2]SkenarioJeffrey M. Howard[3]CeritaJohn LasseterKlay HallJeffrey M. HowardPemeranDane CookStacy KeachPriyanka ChopraBrad GarrettCedric the EntertainerJulia Louis-DreyfusRoger Craig SmithJohn CleeseCarlos AlazraquiPenata musikMark Mancina[4]PenyuntingJeremy MiltonPerusahaanproduksiWalt Disney PicturesDisneyToon StudiosPixar Animation StudiosDistributorWalt Disney Stu...

 

Gosong pasir

Gosong pasir pasang-surut yang menghubungkan Pulau Waya dan Wayasewa di Kepulauan Yasawa, Fiji. Gumuk pasir di Frisian Utara Laut Wadden (Jerman) Gosong pasir, atau gosong saja, adalah bentukan daratan yang terkurung atau menjorok pada suatu perairan. Gosong biasa terbentuk dari pasir, geluh, atau kerikil. Bentukan geografi ini terjadi akibat adanya aliran dangkal dan sempit sehingga memungkinkan pengendapan material ringan dan mengarah pada pendangkalan tubuh air. Gosong dapat terbentuk di l...

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

コルク

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL（2017年4月） コルクを打ち抜いて作った瓶の栓 コルク（木栓、�...

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

 

Musgrave Park, Brisbane

Musgrave ParkMusgrave Park in South BrisbaneLocationBrisbane, Queensland, AustraliaArea6.3 hectares (16 acres)[1]Created1856 Musgrave Park is a park in South Brisbane, Queensland, Australia. The park is bordered by Edmonstone, Russell, and Cordelia Streets, and Brisbane State High School, and has an area of 63,225 square metres (680,550 sq ft).[1] The park is of cultural significance to Aboriginal Australians. The park and the former bowls clubhouse (now used as a c...

 

Brush rabbit

Species of mammal This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Brush rabbit – news · newspapers · books · scholar · JSTOR (January 2014) (Learn how and when to remove this message) Brush rabbit[1] Brush rabbit (Finley National Wildlife Refuge) Conservation status Least Concern  (IUCN 3.1)[...

KRI Teluk Hading (538)

KRI Teluk Hading (538) Sejarah Jerman Timur Nama CottbusAsal nama CottbusPembangun VEB Peenewerft, WolgastBiaya US$51 Juta (Rp791,34 Miliar)Nomor galangan 338Pasang lunas 22 November 1976Diluncurkan 10 Juni 1977Mulai berlayar 26 Mei 1978Dipensiunkan 2 Oktober 1990Identifikasi Nomor lambung: 634, 614Nasib dijual ke Indonesia 1993 Indonesia Nama Teluk HadingAsal nama Teluk Hading, Kabupaten Flores TimurDiperoleh 25 Agustus 1993Mulai berlayar 12 Juli 1994Identifikasi Nomor lambung: 538Motto Bra...

 

Orang Karen

Karen ကညီPerempuan Karen dengan Baju tradisionalDaerah dengan populasi signifikan Myanmar7,000,000[1] Thailand1,000,000[2] USA70,000+ Australia11,000+[3] Canada5,000[4] Sweden1,500Negara Lain100,000+BahasaKaren languages, termasuk S'gaw Karen, Pwo Karen, Karenni dan Pa'OAgamaChristianity, Theravada Buddhism, Animism Pusat Karen di Myanmar Orang Karen mengacu kepada beberapa kelompok bahasa etnis Sino-Tibet, banyak yang tidak ...

 

Hans Kelsen

Hans KelsenFonctionMember of the Constitutional Court of AustriaBiographieNaissance 11 octobre 1881PragueDécès 19 avril 1973 (à 91 ans)BerkeleyÉpoque Philosophie du XXe siècle (d)Nationalités autrichienne (11 octobre 1881 - 1918)autrichienne (1918-1936)tchécoslovaque (à partir de 1936)américaine (à partir du 28 juillet 1945)Formation Université de VienneUniversité de HeidelbergUniversité HarvardAkademisches GymnasiumActivités Avocat, professeur d'université, philosophe, ju...

Confine tra la Malaysia e Singapore

Confine tra la Malaysia e SingaporeCollegamento stradale Johor–Singapore visto dal punto di controllo Woodlands a Singapore verso Johor Bahru, Malesia nel 2006. La fine del territorio di Singapore e l'inizio del territorio malese possono essere chiaramente viste con le differenze nella superficie stradale e nei segni vicino alla sezione centrale della strada. Il vecchio complesso CIQ Johor Bahru è stato sostituito dal Sultan Iskandar Building 1 km nell'entroterra nel 2008.Dati general...

 

Bundesstraße 5

Dieser Artikel beschreibt die Bundesstraße 5 in Deutschland. Zur gleichnamigen Straße in Österreich siehe Waidhofener Straße. Vorlage:Infobox hochrangige Straße/Wartung/DE-B Bundesstraße 5 in Deutschland Karte Verlauf der B 5 Alle Koordinaten: OSM | WikiMap Basisdaten Betreiber: Deutschland Bundesrepublik Deutschland Straßenbeginn: Ellhöft(54° 54′ 14″ N, 8° 54′ 37″ O54.903858.910308) Straßenende: Frankfurt (Oder)(52° 2...

 

Jakob Friedrich Fries

German philosopher and mathematician (1773–1843) Jakob Friedrich FriesBorn23 August 1773 (1773-08-23)Barby (present-day Saxony-Anhalt, Germany)Died10 August 1843 (1843-08-11) (aged 69)Jena (present-day Thuringia, Germany)Alma materUniversity of LeipzigUniversity of JenaEra19th-century philosophyRegionWestern philosophySchoolPost-Kantianism[1]InstitutionsUniversity of JenaMain interestsMetaphysicsPsychologyPhilosophy of science[2]Philosophical logicNotable...

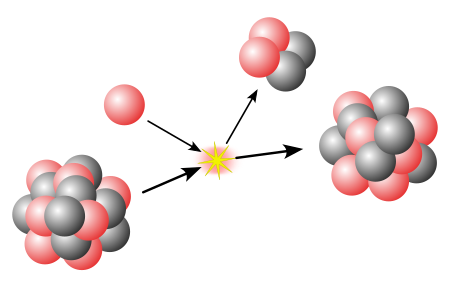
Spontaneous fission

Form of radioactive decay Nuclear physics Nucleus Nucleons p n Nuclear matter Nuclear force Nuclear structure Nuclear reaction Models of the nucleus Liquid drop Nuclear shell model Interacting boson model Ab initio Nuclides' classification Isotopes – equal Z Isobars – equal A Isotones – equal N Isodiaphers – equal N − Z Isomers – equal all the above Mirror nuclei – Z ↔ N Stable Magic Even/odd Halo Borromean Nuclear stability Binding energy p–n ratio Drip line ...

 

Tristan Tzara

Romanian-French poet (1896–1963) Tristan TzaraPortrait of Tristan Tzara, by Robert Delaunay (1923)BornSamuel (Samy) Rosenstock28 April 1896Moinești, RomaniaDied25 December 1963(1963-12-25) (aged 67)Paris, FrancePen nameS. Samyro, Tristan, Tristan Ruia, Tristan Țara, Tr. TzaraOccupationPoet, essayist, journalist, playwright, performance artist, composer, film director, politician, diplomatNationalityRomanianPeriod1912–1963GenreLyric poetry, epic poetry, free verse, prose poetry, par...