Non-Hermitian quantum mechanics

In physics, non-Hermitian quantum mechanics describes quantum mechanical systems where Hamiltonians are not Hermitian.

History

The first paper that has "non-Hermitian quantum mechanics" in the title was published in 1996 [1] by Naomichi Hatano and David R. Nelson. The authors mapped a classical statistical model of flux-line pinning by columnar defects in high-Tc superconductors to a quantum model by means of an inverse path-integral mapping and ended up with a non-Hermitian Hamiltonian with an imaginary vector potential in a random scalar potential. They further mapped this into a lattice model and came up with a tight-binding model with asymmetric hopping, which is now widely called the Hatano-Nelson model. The authors showed that there is a region where all eigenvalues are real despite the non-Hermiticity.

Parity–time (PT) symmetry was initially studied as a specific system in non-Hermitian quantum mechanics.[2][3] In 1998, physicist Carl Bender and former graduate student Stefan Boettcher published a paper[4] where they found non-Hermitian Hamiltonians endowed with an unbroken PT symmetry (invariance with respect to the simultaneous action of the parity-inversion and time reversal symmetry operators) also may possess a real spectrum. Under a correctly-defined inner product, a PT-symmetric Hamiltonian's eigenfunctions have positive norms and exhibit unitary time evolution, requirements for quantum theories.[5] Bender won the 2017 Dannie Heineman Prize for Mathematical Physics for his work.[6]

A closely related concept is that of pseudo-Hermitian operators, which were considered by physicists Paul Dirac,[7] Wolfgang Pauli,[8] and Tsung-Dao Lee and Gian Carlo Wick.[9] Pseudo-Hermitian operators were discovered (or rediscovered) almost simultaneously by mathematicians Mark Krein and collaborators[10][11][12][13] as G-Hamiltonian[clarification needed] in the study of linear dynamical systems. The equivalence between pseudo-Hermiticity and G-Hamiltonian is easy to establish.[14]

In the early 1960s, Olga Taussky, Michael Drazin, and Emilie Haynsworth demonstrated that the necessary and sufficient criteria for a finite-dimensional matrix to have real eigenvalues is that said matrix is pseudo-Hermitian with a positive-definite metric. [15] [16] In 2002, Ali Mostafazadeh showed that diagonalizable PT-symmetric Hamiltonians belong to the class of pseudo-Hermitian Hamiltonians.[17][18][19] In 2003, it was proven that in finite dimensions, PT-symmetry is equivalent to pseudo-Hermiticity regardless of diagonalizability,[20] thereby applying to the physically interesting case of non-diagonalizable Hamiltonians at exceptional points. This indicates that the mechanism of PT-symmetry breaking at exception points, where the Hamiltionian is usually not diagonalizable, is the Krein collision between two eigenmodes with opposite signs of actions.

In 2005, PT symmetry was introduced to the field of optics by the research group of Gonzalo Muga by noting that PT symmetry corresponds to the presence of balanced gain and loss.[21] In 2007, the physicist Demetrios Christodoulides and his collaborators further studied the implications of PT symmetry in optics.[22][23] The coming years saw the first experimental demonstrations of PT symmetry in passive and active systems.[24][25] PT symmetry has also been applied to classical mechanics, metamaterials, electric circuits, and nuclear magnetic resonance.[26][22] In 2017, a non-Hermitian PT-symmetric Hamiltonian was proposed by Dorje Brody and Markus Müller that "formally satisfies the conditions of the Hilbert–Pólya conjecture."[27][28]

References

  1. ^ Hatano, Naomichi; Nelson, David R. (1996-07-15). "Localization Transitions in Non-Hermitian Quantum Mechanics". Physical Review Letters. 77 (3): 570–573. arXiv:cond-mat/9603165. Bibcode:1996PhRvL..77..570H. doi:10.1103/PhysRevLett.77.570. S2CID 43569614.
  2. ^ N. Moiseyev, "Non-Hermitian Quantum Mechanics", Cambridge University Press, Cambridge, 2011
  3. ^ "Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects". Wiley.com. 2015-07-20. Retrieved 2018-06-12.
  4. ^ Bender, Carl M.; Boettcher, Stefan (1998-06-15). "Real Spectra in Non-Hermitian Hamiltonians Having $\mathsc{P}\mathsc{T}$ Symmetry". Physical Review Letters. 80 (24): 5243–5246. arXiv:physics/9712001. Bibcode:1998PhRvL..80.5243B. doi:10.1103/PhysRevLett.80.5243. S2CID 16705013.
  5. ^ Bender, Carl M. (2007). "Making sense of non-Hermitian Hamiltonians". Reports on Progress in Physics. 70 (6): 947–1018. arXiv:hep-th/0703096. Bibcode:2007RPPh...70..947B. doi:10.1088/0034-4885/70/6/R03. ISSN 0034-4885. S2CID 119009206.
  6. ^ "Dannie Heineman Prize for Mathematical Physics".
  7. ^ Dirac, P. A. M. (18 March 1942). "Bakerian Lecture - The physical interpretation of quantum mechanics". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 180 (980): 1–40. Bibcode:1942RSPSA.180....1D. doi:10.1098/rspa.1942.0023.
  8. ^ Pauli, W. (1 July 1943). "On Dirac's New Method of Field Quantization". Reviews of Modern Physics. 15 (3): 175–207. Bibcode:1943RvMP...15..175P. doi:10.1103/revmodphys.15.175.
  9. ^ Lee, T.D.; Wick, G.C. (February 1969). "Negative metric and the unitarity of the S-matrix". Nuclear Physics B. 9 (2): 209–243. Bibcode:1969NuPhB...9..209L. doi:10.1016/0550-3213(69)90098-4.
  10. ^ M. G. Krein, “A generalization of some investigations of A. M. Lyapunov on linear differential equations with periodic coefficients,” Dokl. Akad. Nauk SSSR N.S. 73, 445 (1950) (Russian).
  11. ^ M. G. Krein, Topics in Differential and Integral Equations and Operator Theory (Birkhauser, 1983).
  12. ^ I. M. Gel’fand and V. B. Lidskii, “On the structure of the regions of stability of linear canonical systems of differential equations with periodic coefficients,” Usp. Mat. Nauk 10:1(63), 3−40 (1955) (Russian).
  13. ^ V. Yakubovich and V. Starzhinskii, Linear Differential Equations with Periodic Coefficients (Wiley, 1975), Vol. I.
  14. ^ Zhang, Ruili; Qin, Hong; Xiao, Jianyuan (2020-01-01). "PT-symmetry entails pseudo-Hermiticity regardless of diagonalizability". Journal of Mathematical Physics. 61 (1): 012101. arXiv:1904.01967. Bibcode:2020JMP....61a2101Z. doi:10.1063/1.5117211. ISSN 0022-2488. S2CID 102483351.
  15. ^ Taussky, Olga; Parker, W. (1960). "Problem 4846". The American Mathematical Monthly. 67 (2): 192–193. doi:10.2307/2308556.
  16. ^ Drazin, Michael (1962). "Criteria for the reality of matrix eigenvalues". Mathematische Zeitschrift. 78 (1): 449–452. doi:10.1007/BF01195188.
  17. ^ Mostafazadeh, Ali (2002). "Pseudo-Hermiticity versus symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian". Journal of Mathematical Physics. 43 (1): 205–214. arXiv:math-ph/0107001. Bibcode:2002JMP....43..205M. doi:10.1063/1.1418246. ISSN 0022-2488. S2CID 15239201.
  18. ^ Mostafazadeh, Ali (2002). "Pseudo-Hermiticity versus PT-symmetry. II. A complete characterization of non-Hermitian Hamiltonians with a real spectrum". Journal of Mathematical Physics. 43 (5): 2814–2816. arXiv:math-ph/0110016. Bibcode:2002JMP....43.2814M. doi:10.1063/1.1461427. ISSN 0022-2488. S2CID 17077142.
  19. ^ Mostafazadeh, Ali (2002). "Pseudo-Hermiticity versus PT-symmetry III: Equivalence of pseudo-Hermiticity and the presence of antilinear symmetries". Journal of Mathematical Physics. 43 (8): 3944–3951. arXiv:math-ph/0107001. Bibcode:2002JMP....43.3944M. doi:10.1063/1.1489072. ISSN 0022-2488. S2CID 7096321.
  20. ^ Scolarici, G. (2003-10-01). "On the pseudo-Hermitian nondiagonalizable Hamiltonians". Journal of Mathematical Physics. 44 (10): 4450–4459. arXiv:quant-ph/0211161. doi:10.1063/1.1609031.
  21. ^ Ruschhaupt, A; Delgado, F; Muga, J G (2005-03-04). "Physical realization of -symmetric potential scattering in a planar slab waveguide". Journal of Physics A: Mathematical and General. 38 (9): L171–L176. arXiv:1706.04056. doi:10.1088/0305-4470/38/9/L03. ISSN 0305-4470. S2CID 118099017.
  22. ^ a b Bender, Carl (April 2016). "PT symmetry in quantum physics: from mathematical curiosity to optical experiments". Europhysics News. 47, 2 (2): 17–20. Bibcode:2016ENews..47b..17B. doi:10.1051/epn/2016201.
  23. ^ Makris, K. G.; El-Ganainy, R.; Christodoulides, D. N.; Musslimani, Z. H. (2008-03-13). "Beam Dynamics in $\mathcal{P}\mathcal{T}$ Symmetric Optical Lattices". Physical Review Letters. 100 (10): 103904. Bibcode:2008PhRvL.100j3904M. doi:10.1103/PhysRevLett.100.103904. PMID 18352189.
  24. ^ Guo, A.; Salamo, G. J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G. A.; Christodoulides, D. N. (2009-08-27). "Observation of $\mathcal{P}\mathcal{T}$-Symmetry Breaking in Complex Optical Potentials". Physical Review Letters. 103 (9): 093902. Bibcode:2009PhRvL.103i3902G. doi:10.1103/PhysRevLett.103.093902. PMID 19792798.
  25. ^ Rüter, Christian E.; Makris, Konstantinos G.; El-Ganainy, Ramy; Christodoulides, Demetrios N.; Segev, Mordechai; Kip, Detlef (March 2010). "Observation of parity–time symmetry in optics". Nature Physics. 6 (3): 192–195. Bibcode:2010NatPh...6..192R. doi:10.1038/nphys1515. ISSN 1745-2481.
  26. ^ Miller, Johanna L. (October 2017). "Exceptional points make for exceptional sensors". Physics Today. 10, 23 (10): 23–26. Bibcode:2017PhT....70j..23M. doi:10.1063/PT.3.3717.
  27. ^ Bender, Carl M.; Brody, Dorje C.; Müller, Markus P. (2017-03-30). "Hamiltonian for the Zeros of the Riemann Zeta Function". Physical Review Letters. 118 (13): 130201. arXiv:1608.03679. Bibcode:2017PhRvL.118m0201B. doi:10.1103/PhysRevLett.118.130201. PMID 28409977. S2CID 46816531.
  28. ^ "Quantum Physicists Attack the Riemann Hypothesis | Quanta Magazine". Quanta Magazine. Retrieved 2018-06-12.

Read other articles:

Ruskin Monument

Monument to John Ruskin in Keswick, Cumbria, UK Ruskin MonumentArtistMr. Bromley and his nephew, stonecuttersYear1900MediumBorrowdale slateDesignationGrade IILocationKeswick, CumbriaCoordinates54°35′25″N 3°08′28″W / 54.59033°N 3.14098°W / 54.59033; -3.14098 Listed Building – Grade IIDesignated24 May 1977Reference no.1327119[1] Websitehttps://historicengland.org.uk/listing/the-list/list-entry/1327119 The Ruskin Monument is a memorial to John R...

 

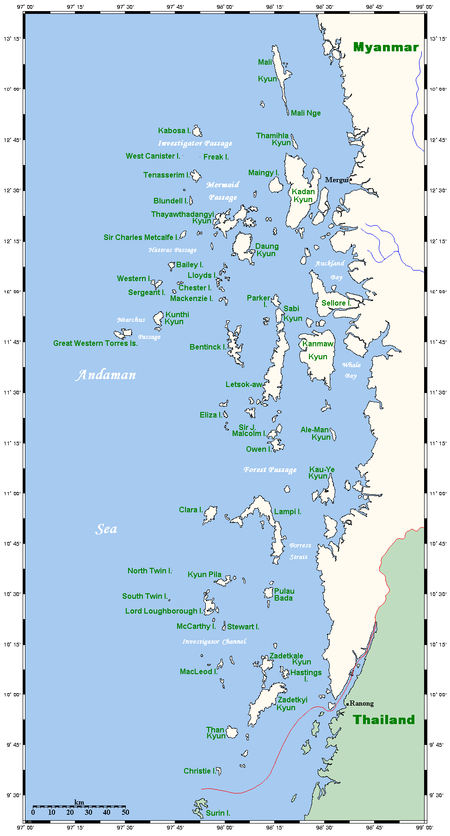
Archipelago

Collection of islands Island chain redirects here. For the strategy, see Island chain strategy. For other uses, see Archipelago (disambiguation). Not to be confused with arpeggio or a cappella. The Aegean Sea with its large number of islands is the origin of the term archipelago. The Mergui Archipelago in Myanmar An archipelago (/ˌɑːrkəˈpɛləɡoʊ/ ⓘ AR-kə-PEL-ə-goh),[1] sometimes called an island group or island chain, is a chain, cluster, or collection of islands, or s...

 

Reza Artamevia

Reza ArtameviaReza pada tahun 2017LahirReza Artamevia Adriana Eka Suci29 Mei 1975 (umur 48)Jakarta, IndonesiaKebangsaanIndonesiaNama lainReza ArtameviraAlmamaterUniversitas PancasilaPekerjaanPenyanyiaktrispolitikusTahun aktif1992–sekarangPartai politikNasDem (2023–sekarang)Perindo (2019–2023)Suami/istriAdjie Massaid ​ ​(m. 1999; c. 2005)​Anak2, termasuk Aaliyah MassaidKarier musikGenreR&Bsoulpop rockInstrumenVokal Label...

David Bushnell

American inventor who built the Turtle submersible (1740–1824/1826) For the historian, see David Bushnell (historian). For the entrepreneur, see David P. Bushnell. David BushnellBorn(1740-08-30)August 30, 1740Westbrook, ConnecticutDied1824/1826WarrentonNationalityAmericanOccupationInventorKnown forBuilding Turtle submersible A diagram of Bushnell's American Turtle David Bushnell (August 30, 1740 – 1824 or 1826), of Westbrook, Connecticut, was an American inventor, a patriot, a teache...

 

Steve Keen

Steve KeenSteve Keen.BiographieNaissance 28 mars 1953 (71 ans)SydneyNationalité AustralienneFormation Université de SydneyActivité ÉconomisteAutres informationsA travaillé pour Université occidentale de Sydney (1996-2013)Université KingstonInfluencé par Hyman Minsky, Joseph Schumpeter, John Maynard Keynes, Piero Sraffa, Karl Marx, Augusto Graziani, Thorstein Veblen, François QuesnayŒuvres principales Debunking Economics (d)modifier - modifier le code - modifier Wikidata Steve K...

 

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

The Age of Innocence (film 1993)

Untuk kegunaan lain, lihat The Age of Innocence. The Age of InnocenceTheatrical release posterSutradaraMartin ScorseseProduserBarbara De FinaSkenarioJay CocksMartin ScorseseBerdasarkanThe Age of Innocenceoleh Edith WhartonPemeran Daniel Day-Lewis * Michelle Pfeiffer * Winona Ryder NaratorJoanne WoodwardPenata musikElmer BernsteinSinematograferMichael BallhausPenyuntingThelma SchoonmakerDistributorColumbia PicturesTanggal rilis 17 September 1993 (1993-09-17) Durasi139 minutesNegaraU...

 

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

Bukhori Yusuf

Bukhori YusufBukhori Yusuf sebagai Calon Anggota Legislatif DPR RI dari Partai Keadilan Sejahtera untuk Pemilihan Umum Legislatif tahun 2019 Anggota Dewan Perwakilan RakyatRepublik IndonesiaMasa jabatan1 Oktober 2019 – Mei 2023Perolehan suara52.790 (2019)[1]PenggantiWisnu Wijaya Adi PutraDaerah pemilihanJawa Tengah IMasa jabatan1 Oktober 2009 – 30 September 2014Daerah pemilihanSumatera Selatan II Informasi pribadiLahir5 Maret 1965 (umur 59)Jepara, Jawa Tenga...

Oleoylethanolamide

Oleoylethanolamide Names Preferred IUPAC name (9Z)-N-(2-Hydroxyethyl)octadec-9-enamide Identifiers CAS Number 111-58-0 Y 3D model (JSmol) Interactive image ChEBI CHEBI:77362 ChemSpider 4446574 N ECHA InfoCard 100.003.532 IUPHAR/BPS 2661 PubChem CID 5283454 UNII 1HI5J9N8E6 Y CompTox Dashboard (EPA) DTXSID1044516 InChI InChI=1S/C20H39NO2/c1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-20(23)21-18-19-22/h9-10,22H,2-8,11-19H2,1H3,(H,21,23)/b10-9- NKey: BOWVQLFMWHZBEF-KTKRTIGZ...

 

المكتبة الوطنية الباكستانية

المكتبة الوطنية الباكستانية إحداثيات 33°43′36″N 73°06′06″E / 33.726696°N 73.101736°E / 33.726696; 73.101736   معلومات عامة الدولة جمهورية باكستان الإسلامية سنة التأسيس 1951 النوع مكتبة وطنية  معلومات أخرى الموقع الإلكتروني الموقع الرسمي تعديل مصدري - تعديل   المكتبة الوطنية ال...

 

Snowy Road

Snowy RoadPoster teatrikalNama lainHangul눈길 Alih Aksara yang DisempurnakanNungil SutradaraLee Na-jeongProduserHam Yeong-hunDitulis olehYoo Bo-raPemeranKim Sae-ron Kim Hyang-giPenata musikNam Hye-seungSinematograferPark SungPenyuntingKim Young-juPerusahaanproduksiKBSat9 FilmsDistributorCGV ArthouseTanggal rilis Mei 2015 (2015-05) (JIFF) 01 Maret 2017 (2017-03-01) Durasi122 menitNegaraKorea SelatanBahasaKoreanJepangPendapatankotorUS$866,692[1] Snowy Road (H...

FC Encamp

FC EncampNama lengkapFútbol Club EncampJulukan-Berdiri1950StadionEstadio Comunal de AixovallAndorra la Vella Andorra(Kapasitas: 1,800)KetuaSalvador Cervos PiaManajer>Liga2.a Divisió2021–22Segona Divisió, 6. Kostum kandang Kostum tandang FC Encamp adalah Andorra n sepak bola klub yang berbasis di Encamp. Untuk musim 2007/08 mereka telah diturunkan ke Segona Divisió, divisi 2 terbaik. Pada 2008/09, mereka dipromosikan kembali ke Primera Divisió. Prestasi Campionat de Lliga: 2 1996, 20...

 

Emidio Taliani

Emidio TalianiKardinal-Imam San Bernardo alle TermeTaliani pada 1895.GerejaGereja Katolik RomaPenunjukan12 November 1903Masa jabatan berakhir24 Agustus 1907PendahuluGiuseppe Melchiorre SartoPenerusPietro GasparriImamatTahbisan imam20 Oktober 1861Tahbisan uskup29 Juni 1896oleh Lucido Maria ParocchiPelantikan kardinal22 Juni 1903oleh Paus Leo XIIIPeringkatKardinal-ImamInformasi pribadiNama lahirEmidio TalianiLahir19 April 1838Montegallo, Negara GerejaWafat24 Agustus 1907(1907-08-24) (umur&...

 

Courts of Indiana

Courts of Indiana include: State courts of Indiana The E. Ross Adair Federal Building, seat of the Fort Wayne division of the U.S. District Court for the Northern District of Indiana Indiana Supreme Court[1] Indiana Court of Appeals (5 districts; previously Indiana Appellate Court)[2] Indiana Tax Court[3] Indiana Circuit Courts (91 circuits)[4][5] Indiana Superior Courts (177 divisions)[4][5] Indiana city and town courts[4][5...

Jerman Barat

Halaman ini berisi artikel tentang Republik Federal Jerman pada tahun 1949 hingga 1990. Untuk Republik Federal Jerman setelah penyatuan kembali, lihat Jerman. Untuk Republik Federal Jerman pada 1919 hingga 1933, lihat Republik Weimar. Republik Federal JermanBundesrepublik Deutschland1949–1990 Bendera Lambang Semboyan: Einigkeit und Recht und Freiheit Persatuan dan keadilan dan kebebasanLagu kebangsaan: Ich hab' mich ergeben(Saya menyerah atas kelakuannya diri sendiri)(1949–1952)...

 

San Wai (San Tin)

For other places with the same name, see San Wai. Hon Lo (漢廬), at No. 61 San Wai Tsuen, is a residence built in 1931. Nos. 35 and 36 San Wai Tsuen, built in 1932. San Wai (Chinese: 新圍) or San Wai Tsuen (新圍村) is a village in the San Tin area of Yuen Long District, Hong Kong. Administration San Wai is one of the villages represented within the San Tin Rural Committee. For electoral purposes, San Wai is part of the San Tin constituency, which is currently represented by Man Fu-...

 

Big Apple

54th and Broadway The Big Apple adalah julukan untuk Kota New York, Amerika Serikat. Julukan ini pertama dipopulerkan pada 1920-an oleh John J. Fitz Gerald, seorang penulis berita olahraga untuk New York Morning Telegraph. Popularitasnya sejak 1970-an terjadi karena kampanye promosi oleh New York Convention and Visitors Bureau yang sekarang bernama NYC & Company. Kota lain Manhattan, Kansas, menyebut dirinya The Little Apple pada karya promosinya. Minneapolis, Minnesota menyebut dirinya T...

Constitutional Charter of 1826

Second constitution in Portuguese history King Pedro IV of Portugal holding the Constitutional Charter. The monument is in Porto. The Charter of 1826 or Carta Constitucional, often simply referred to as the Carta, was the second constitution in Portuguese history. It was given to the country in 1826 by King Dom Pedro IV. The constitution remained in force, with the exceptions of the periods 1828–1834 and 1838–1842, until the fall of the monarchy in 1910.[1] It was modified in 1852...

 

Chronologie de l'invasion de l'Ukraine par la Russie (juillet 2023)

Pour un article plus général, voir Invasion de l'Ukraine par la Russie. Cet article fait partie de la chronologie de l'invasion de l'Ukraine par la Russie et présente une chronologie des événements clés de ce conflit durant le mois de juillet 2023. Pour les événements précédents, voir Chronologie de l'invasion de l'Ukraine par la Russie (juin 2023). Pour les événements suivants, voir Chronologie de l'invasion de l'Ukraine par la Russie (août 2023). Invasion de l'Ukraine en carte...