Localized molecular orbitals
|
Read other articles:

American dairy cooperative Northwest Dairy AssociationDarigold corporate offices in SeattleTrade nameDarigoldCompany typeAgricultural marketing cooperativeIndustryAgricultureFounded1918HeadquartersSeattle, Washington, USArea servedWashington, Oregon, Idaho, California, Utah, Nevada, and HawaiiWebsitedarigold.com Northwest Dairy Association (formerly the Northwest Dairymen's Association; trading as Darigold, Inc.) is an American dairy agricultural marketing cooperative. Headquartered in Seattl...

Bristol RoversNama lengkapBristol RoversJulukanThe Pirates, The GasBerdiri1883; 140 tahun lalu (1883) (sebagai the Black Arabs)StadionMemorial StadiumHorfield, Bristol(Kapasitas: 12,011 (2,500 tempat duduk)[1])KetuaNick Higgs[2]ManagerJohn WardLigaLiga Dua Inggris2012–13ke-14, Liga Dua InggrisPencetak gol terbanyakGeoff Bradford (242) Kostum kandang Kostum tandang Musim ini Bristol Rovers Football Club adalah klub sepak bola profesional Inggris yang berbasis di kota Bri...

Pour les articles homonymes, voir DR1. DR1CaractéristiquesCréation 2 octobre 1951Propriétaire DRSlogan Vi mødes på DR1 ! (litt.) Rendez-vous sur DR1! Nous nous retrouvons sur DR1 !Langue DanoisPays DanemarkStatut Généraliste nationale publiqueSiège social CopenhagueAncien nom Statsradiofonien Fjersyn (1951-1959)DR TV (1959-1996)Site web http://www.dr.dk/tv/live/dr1DiffusionAire Danemark Suède (sud) Allemagne (Schleswig-Holstein)Diffusion Numérique terrestre, satellite, c�...

The following active airports serve the Edmonton Metropolitan Region in Alberta, Canada.[1][2] Airport names in italics are part of the National Airports System.[3] Communities in parentheses () indicates the airport is not in a community. Location of the Edmonton Metropolitan Region in Alberta Land Airport name ICAO/TC LID (IATA) Location Coordinates Edmonton International Airport CYEG (YEG) Nisku, Leduc County 53°18′36″N 113°34′46″W / 53.31...

US Navy salvage ship History United States BuilderBasalt Rock Company Laid down26 October 1942 Launched1 April 1943 Commissioned11 January 1944 Decommissioned23 April 1947 In service1 December 1950 Out of service7 August 1992 Stricken16 March 1994 FateSold for scrap, 30 November 2005 General characteristics Tonnage1,441 tons Displacement1,530 tons Length213 ft 6 in (65.07 m) Beam39 ft (12 m) Draught14 ft 4 in (4.37 m) Propulsiondiesel-electric, twin scr...

King of Babylon Zababa-šuma-iddinaKing of BabylonDetail from unfinished kudurru found at SusaReign1158 BCPredecessorMarduk-apla-iddina ISuccessorEnlil-nādin-aḫeHouseKassite Zababa-šuma-iddina[nb 1] was the 35th and next to last king of the Kassite or 3rd dynasty of Babylon, who reigned for just one year,[i 1] ca. 1158 BC (short chronology). He was without apparent ties to the royal family and there is uncertainty concerning the circumstances of his coming to power. Biogra...

The series Danny Phantom centers on young Danny Fenton and his coming-of-age story as a half-ghost superhero in the town of Amity Park. Over the course of the series, he betters both himself and his powers as he deals with ghosts, balancing his normal and heroic life[1][2] in a community that does not initially trust him.[3] His companions are his best friends: Sam Manson, a vegetarian goth girl who is entranced by the weird and supernatural and Tucker Foley, a lighth...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Steel roller coaster at Kennywood For the Dreamworld roller coaster formerly named Sky Rocket, see Escape from Madagascar. Sky RocketKennywoodLocationKennywoodCoordinates40°23′11″N 79°51′53″W / 40.38639°N 79.86472°W / 40.38639; -79.86472StatusOperatingOpening dateJune 29, 2010 (2010-06-29)General statisticsTypeSteelManufacturerPremier RidesLift/launch systemLSM launchHeight95 ft (29 m)Length2,100 ft (640 m)Speed50 mph...

Samsung Galaxy A23Bagian depan Samsung Galaxy A23MerekSamsung GalaxyPembuatSamsung ElectronicsSeriGalaxy A seriesJaringanGSM / HSPA / LTERilis pertama4 Maret 2022; 2 tahun lalu (2022-03-04)PendahuluSamsung Galaxy A22Samsung Galaxy A22 5GTerkaitSamsung Galaxy A13Samsung Galaxy A33 5GSamsung Galaxy A53 5GSamsung Galaxy A73 5GTipePonsel cerdasFaktor bentukSlateDimensi1.645 mm (64,8 in) H 769 mm (30,3 in) W 84 mm (3,3 in) DBerat195 g (6,9 oz)Sistem Ope...
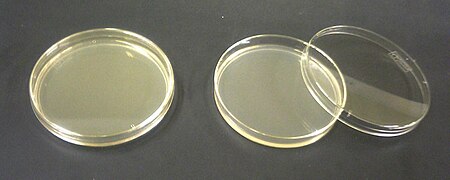
L'agar agar (noto anche come agar, dal nome malese delle alghe rosse) è un polisaccaride usato come gelificante naturale e ricavato da alghe rosse appartenenti a diversi generi (tra i quali Gelidium, Gracilaria, Gelidiella, Pterocladia, Sphaerococcus). Dal punto di vista chimico è un polimero costituito principalmente da unità di D-galattosio (è quindi detto poligalattoside). Indice 1 Utilizzo in cucina 2 Altri usi 3 Note 4 Voci correlate 5 Altri progetti 6 Collegamenti esterni Utilizzo i...

Sinagoga vecchia di EssenAlte Synagoge EssenLa sinagoga in una foto del 2014Stato Germania LocalitàEssen Coordinate51°27′23.04″N 7°01′00.01″E / 51.4564°N 7.01667°E51.4564; 7.01667Coordinate: 51°27′23.04″N 7°01′00.01″E / 51.4564°N 7.01667°E51.4564; 7.01667 ReligioneEbraismo ArchitettoEdmund Körner Stile architettonicoArt Nouveau e neoromanico Modifica dati su Wikidata · Manuale La Sinagoga vecchia di Essen, costruita nel 1913...

Sisters of the SunEpisode Cosmos: A Spacetime OdysseyNomor episodeEpisode 8SutradaraBrannon BragaPenulisAnn DruyanSteven SoterNaratorNeil deGrasse TysonProduserLivia HanichSteven HoltzmanMusikAlan SilvestriPenyuntingJohn DuffyMichael O'HalloranEric LeaTanggal siar27 April 2014 (2014-04-27)Durasi44 menitBintang tamu Kirsten Dunst sebagai Cecilia Payne Marlee Matlin sebagai Annie Jump Cannon Kronologi episode ← SebelumnyaThe Clean Room Selanjutnya →The Electric Boy Daftar epi...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (نوفمبر 2020) اليهودية الإنسانية ((بالعبرية: יהדות הומניסטית) (ياهادوت أنسانيتيستيت) هي �...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Джило Высшая точка Абсолютная высота4116 м Расположение 37°29′09″ с. ш. 44°00′15″ в. д.HGЯO Страна Турция ИльХаккяри Горная системаВосточный Тавр Джило Джило — третья по высоте гора в Турции (4116 м)[1][2]. Расположена в Восточном Тавре в районе Юксекова в...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019)Learn how and when to remove this message كأس مولدوفا 2008–09 تفاصيل الموسم كأس مولدوفا النسخة 18 البلد مولدوفا التار...

دروجكيفكا (بالأوكرانية: Дружківка) دروجكيفكا (فولغوغراد) دروجكيفكا (فولغوغراد) تاريخ التأسيس 1781 تقسيم إداري البلد أوكرانيا [1] خصائص جغرافية إحداثيات 48°37′13″N 37°31′40″E / 48.620277777778°N 37.527777777778°E / 48.620277777778; 37.527777777778 [2] المساحة 46.53 كيلوم...

لمعانٍ أخرى، طالع الرفيق (توضيح). هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. جزء من سلسلة مقالات حولالله في الإسلام مصطلحاتالتسبيح: سبحان الله التكبير: الله أكبر الحمد: الحمد لله التشهّد: لا إله إلّا الله تعابير �...

American federal law enacted in 1882 For Chinese Exclusion Act in Canada, see Chinese Immigration Act, 1923. Not to be confused with Immigration Act of 1924. First page of the Chinese Exclusion Act passed by Congress in 1882[1] Chinese Exclusion ActNicknamesChinese Exclusion ActEnacted bythe 47th United States CongressEffectiveMay 6, 1882CitationsPublic lawPub. L.Tooltip Public Law (United States) 47–126Statutes at Large22 Stat. 58, Chap. 126Legislative historyIn...





![{\displaystyle \sum _{i}^{n}[\langle \phi _{i}|{\vec {r}}|\phi _{i}\rangle ]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adb87386c95550dd75b9a10663cced1d70b9fca9)





