Li Ye (mathematician)
|
Read other articles:

1914 battle of the Zaian War 32°51′27″N 05°37′21″W / 32.85750°N 5.62250°W / 32.85750; -5.62250 Battle of El HerriPart of the Zaian WarLocation of the battle shown on a 1953 map.Date13 November 1914LocationEl Herri, near Khénifra, MoroccoResult Zaian victoryBelligerents France Zaian ConfederationCommanders and leaders René Laverdure † Mouha ou Hammou ZayaniStrength 43 officers and 1,187 men[1] Estimated by the French at 5,000 tribe...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Negara bagian dan wilayah federal di Malaysia – berita · surat kabar · buku · cendekiawan · JSTOR Pembagian administratif Malaysia Tingkat I Negara bagian • Wilayah persekutuan Tingkat II Distrik &...

Bandar Udara LloydminsterBandar Udara LloydminsterIATA: YLLICAO: CYLLWMO: 71871InformasiJenisPublicPengelolaCity of LloydminsterMelayaniLloydminster, AlbertaKetinggian dpl699 mdplSitus webwww.lloydminster.ca/airport.htmlPetaCYLLLokasi di AlbertaLandasan pacu Arah Panjang Permukaan kaki m 08/26 5,579 1,700 Asphalt 12/30 1,500 457 Turf Statistik (2010)Pergerakan pesawat12,857Sumber: Canada Flight Supplement[1]Environment Canada[2]Movements from Statistics Canada[3&...

Ajaccio Aiacciu BenderaLambang kebesaranAjaccio Lokasi di Region Korsika Ajaccio Koordinat: 41°55′36″N 8°44′13″E / 41.9267°N 8.7369°E / 41.9267; 8.7369NegaraPrancisRegionKorsikaDepartemenCorse-du-SudArondisemenAjaccioAntarkomunePays AjaccienPemerintahan • Wali kota (2008–2014) Simon RenucciLuas • Land182,03 km2 (3,167 sq mi) • Populasi265.153 • Kepadatan Populasi27,9/km2 (21/sq mi)Kode IN...
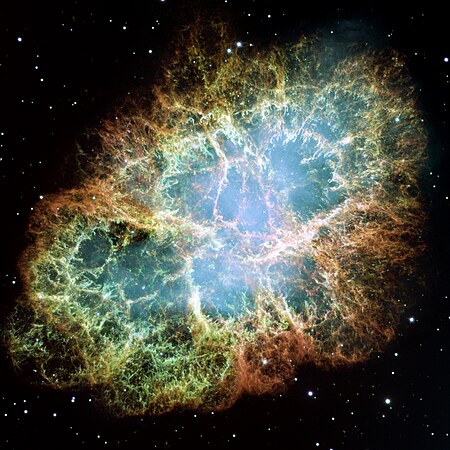
Bagian dari seriKosmologi fisik Ledakan Dahsyat · Alam semesta Umur alam semesta Kronologi alam semesta Alam semesta awal Masa Planck Masa penyatuan agung Nukleosintesis Big Bang Inflasi Zaman Kegelapan Latar belakang Cosmic background radiation (CBR) Gravitational wave background (GWB) Cosmic microwave background (CMB) · Cosmic neutrino background (CNB) Cosmic infrared background (INB) Ekspansi · Masa depan Hukum Hubble · Pergeseran merah Ekspansi alam semesta Metrik ...

لمعانٍ أخرى، طالع تصفيات كأس العالم 2002 (توضيح). تصفيات كأس العالم 2002تفاصيل المسابقةالتواريخ4 مارس 2000 – 25 نوفمبر 2001الفرق199إحصائيات المسابقةالمباريات الملعوبة777الأهداف المسجلة2٬452 (3٫16 لكل مباراة)→ 1998 2006 ← منتخبات تأهلت لكاس العالم منتخبات فشلت في ا...

الاتحاد السويدي لكرة القدم الاسم المختصر SvFF الرياضة كرة القدم أسس عام 1904 (منذ 120 سنة) المقر بلدية سولنا الانتسابات الفيفا : 1904 اليويفا : 1954 رمز الفيفا GEO الموقع الرسمي www.svenskfotboll.se تعديل مصدري - تعديل تأسس الاتحاد السويدي لكرة القدم (بالسويدية: Svenska Fotbollförbundet) في...

Shawn AshmoreLahirShawn Robert Ashmore7 Oktober 1979 (umur 44)Richmond, British Columbia, KanadaPekerjaanAktorTahun aktif1991 – sekarang Shawn Robert Ashmore (lahir 7 Oktober 1979)[1] adalah aktor asal Kanada. Ia dikenal karena perannya sebagai Jake dalam serial televisi Animorphs dan Iceman dalam film X-Men. Ia adalah saudara kembar dari aktor Aaron Ashmore. Filmografi Film Tahun Film Peran Catatan 1991 Married to It Student in pageant 1993 Gross Misconduct young Brian S...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Pemilihan Member Single ke-10 JKT48Logo Pemilihan Member Single ke-10 JKT48 bersama Honda The Power of DreamsTanggal26 Maret 2015 - 30 April 2015 (pemungutan suara)2 Mei 2015 (...

British physicist For other people named Paul Davies, see Paul Davies (disambiguation). Paul DaviesAMDavies in 2016BornPaul Charles William Davies (1946-04-22) 22 April 1946 (age 77)London, United KingdomAlma materUniversity College LondonKnown forFulling–Davies–Unruh effectBunch–Davies vacuum stateMoving MirrorsAwardsTempleton Prize (1995)Kelvin Medal (2001)Faraday Prize (2002)Klumpke-Roberts Award (2011)Scientific careerFieldsPhysicsInstitutionsArizona State UniversityU...

سيرغي أوستابينكو معلومات شخصية الميلاد 23 فبراير 1986 (العمر 38 سنة)ألماتي الطول 1.90 م (6 قدم 3 بوصة) مركز اللعب مهاجم الجنسية كازاخستان الرقم 21 مسيرة الشباب سنوات فريق FC Alma-Ata [الإنجليزية] المسيرة الاحترافية1 سنوات فريق م. (هـ.) 2003−2006 FC Alma-Ata [الإنجليزية] 98 (21)...

American politician For the NYPD Police Commissioner, see Douglas Imrie McKay. For the ice hockey player, see Doug McKay. For the Australian cricketer, see Douglas McKay (cricketer). Douglas McKay35th United States Secretary of the InteriorIn officeJanuary 21, 1953 – April 15, 1956PresidentDwight D. EisenhowerPreceded byOscar L. ChapmanSucceeded byFred A. Seaton25th Governor of OregonIn officeJanuary 10, 1949 – December 27, 1952Preceded byJohn HallSucceeded byPaul L. Pat...

Van Cliburn nel 1962 a Caesarea in Israele. 2 volte vincitore ai Grammy awards Van Cliburn, pseudonimo di Harvey Lavan Cliburn Jr. (Shreveport, 12 luglio 1934 – Fort Worth, 27 febbraio 2013), è stato un pianista statunitense. È noto al grande pubblico per aver partecipato al primo Concorso internazionale Čajkovskij (inaugurato a Mosca nel 1958) - la cui giuria era tra gli altri composta anche da giganti della tastiera quali Svjatoslav Richter ed Ėmil' Gilel's[1] - e averlo vinto...

English cricketer and rugby union player John RaphaelRaphael in 1909Personal informationFull nameJohn Edward RaphaelBorn(1882-04-30)30 April 1882Brussels, BelgiumDied11 June 1917(1917-06-11) (aged 35)Rémy, FranceBattingRight-handedBowlingRight-arm slow-mediumRoleBatsmanRelationsRichard Raphael (cousin)Domestic team information YearsTeam1901–1902London County1903–1909Surrey1903–1905Oxford University1905–1913MCC Career statistics Competition First-class Matches 77 Runs scored...

American television series For other uses, see Highway to Heaven (disambiguation). Highway to HeavenGenreFantasyFamily dramaCreated byMichael LandonDirected byMichael LandonVictor FrenchDan GordonWilliam F. ClaxtonStarringMichael LandonVictor FrenchComposerDavid RoseCountry of originUnited StatesOriginal languageEnglishNo. of seasons5No. of episodes111 (list of episodes)ProductionExecutive producerMichael LandonProducerKent McCrayCamera setupSingle-cameraRunning time48–49 minutesProduction ...

SDN 15 BotumoitoSekolah Dasar Negeri 15 BotumoitoInformasiJenisSekolah DasarNomor Pokok Sekolah Nasional40502693Kepala SekolahRahmin Abd. DunggioModeratorNurhayati HilalaJumlah kelas5Rentang kelasI-VIKurikulumkurikulum KTSPStatusNegeriAlamatLokasi, Boalemo, Gorontalo, IndonesiaTel./Faks.081356101330Koordinat0°30′43″N 122°12′48″E / 0.5119350°N 122.2134000°E / 0.5119350; 122.2134000Situs webhttp://pgribotumoito.blogspot.comSurelrahmin.dunggio@y...

State park in Oregon Fogarty Creek State Recreation AreaView of Fogarty Creek, the US Highway 101 overpass, and the Pacific OceanShow map of OregonShow map of the United StatesTypePublic, stateLocationLincoln County, OregonNearest cityLincoln CityCoordinates44°50′32″N 124°02′44″W / 44.842335°N 124.04567°W / 44.842335; -124.04567[1]Area165.08 acres (66.81 ha)[2]Created1950s[3]Operated byOregon Parks and Recreation Fogar...

Ken Kesey's Merry Band of Pranksters' 1960s hippie-bus Motor vehicle FurthurKen Kesey's original Furthur in 1964OverviewTypeSchool busManufacturerInternational HarvesterProduction1939 (1939)AssemblyUnited States Inside Furthur, psychedelic paintings Furthur is a 1939 International Harvester school bus purchased by author Ken Kesey in 1964 to carry his Merry Band of Pranksters cross-country, filming their counterculture adventures as they went. The bus featured prominently in Tom Wolfe's ...

UFC mixed martial arts event in 2010 UFC Fight Night: Maynard vs. DiazThe poster for UFC Fight Night: Maynard vs. DiazInformationPromotionUltimate Fighting ChampionshipDateJanuary 11, 2010VenuePatriot CenterCityFairfax, VirginiaAttendance8,078[1]Total gate$753,962[1]Event chronology UFC 108: Evans vs. Silva UFC Fight Night: Maynard vs. Diaz UFC 109: Relentless UFC Fight Night: Maynard vs. Diaz (also known as UFC Fight Night 20) was a mixed martial arts event held by the Ultima...

30th Army may refer to: 30th Army (People's Republic of China) 30th Army (Soviet Union) Thirtieth Army (Japan), a unit of the Imperial Japanese Army Topics referred to by the same termThis disambiguation page lists articles about military units and formations which are associated with the same title. If an internal link referred you to this page, you may wish to change the link to point directly to the intended article.



