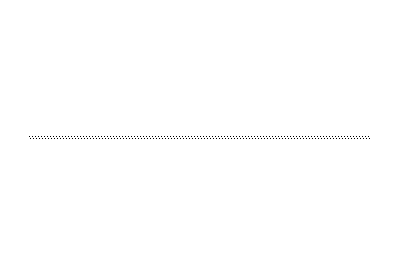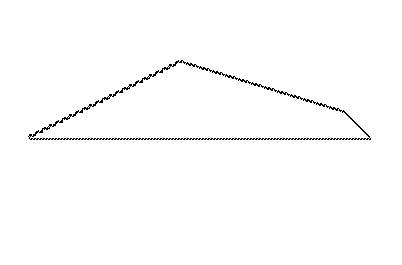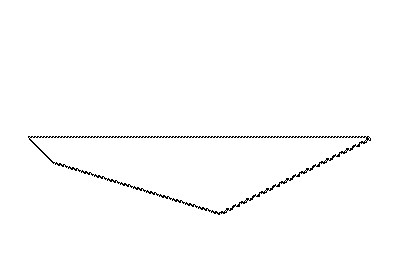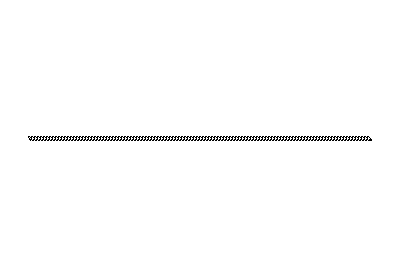Langton's ant
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Amani Swissiأماني السويسيNama lahirAmani SwissiLahir11 April 1983 (umur 40) Sfax, TunisiaGenreMusik ArabPekerjaanpenyanyiaktrisTahun aktif2005 – sekarangLabelRotana Records Amani Swissi (Arab: أماني السويسيcode: ar is de...

All Channels That Available In India (Mixture Of All Dth Like Tata Play, Dish TV, D2h etc.) See also: List of news channels in India This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Hindi television channels – news · newspapers · books · scholar · JSTOR (August 2022) (Learn how and when to remove this template message)...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Football tournament season 1974–75 Coppa ItaliaFiorentina's winning squadTournament detailsCountry ItalyDates28 Aug 1974 – 28 June 1975Teams36Final positionsChampionsFiorentina (4th title)Runner-upMilanTournament statisticsMatches played95Goals scored208 (2.19 per match)Top goal scorer(s)Pierino Prati Pietro Anastasi (8 goals)← 1973–741975–76 → The 1974–75 Coppa Italia was the 28th Coppa Italia, the major Italian domestic cup. The competitio...

Election for the Governor of Vermont 1787 Vermont Republic gubernatorial election ← 1786 October 11, 1787 (1787-10-11) 1788 → Nominee Thomas Chittenden Party Independent Governor before election Thomas Chittenden Independent Elected Governor Thomas Chittenden Independent Elections in Vermont Federal government Presidential elections 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 188...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

Voce principale: Associazione Sportiva Dilettantistica Acireale Calcio. Associazione Sportiva AcquapozzilloStagione 1971-1972Sport calcio Squadra Acquapozzillo Allenatore Francesco Lamberti poi Antonino Abate Presidente Francesco Gravina Serie C15º posto nel girone C. Maggiori presenzeCampionato: Dugaro, Manini (38) Miglior marcatoreCampionato: Frieri (8) 1970-1971 1972-1973 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Sporti...

Borough in Estonia Small borough in Tartu County, EstoniaVarnjaSmall boroughVarnjaLocation in EstoniaCoordinates: 58°29′30″N 27°14′20″E / 58.49167°N 27.23889°E / 58.49167; 27.23889CountryEstoniaCountyTartu CountyMunicipalityPeipsiääre ParishPopulation (2011 Census[1]) • Total171 Drone video of Varnja village in August 2021 Varnja is a small borough (Estonian: alevik) in Peipsiääre Parish, Tartu County, in northeastern Estonia. A...

Cet article est une ébauche concernant une chanson. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Rock 'n' Roll Kids Chanson de Paul Harrington & Charlie McGettigan au Concours Eurovision de la chanson 1994 Sortie 1994 Durée 3:00 Auteur Brendan Graham Compositeur Brendan Graham Chansons représentant l'Irlande au Concours Eurovision de la chanson In Your Eyes(1993) Dreamin'(1995) Chansons ayant remp...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Roman d'Énéas Miniature prise du manuscrit 60 français de la Bibliothèque nationale de France. Auteur Anonyme Pays France Genre Roman Date de parution Environ 1160 modifier Le Roman d'Énéas est un roman anonyme ; la date de rédaction du premier manuscrit est estimée à 1160. On considère ce texte comme un des plus anciens romans français (ou le plus ancien selon la définition que l'on donne au mot « roman »[1]). L'histoire Le Roman d'Énéas est une adaptati...

Croatian footballer (born 1987) Marin Tomasov Tomasov with TSV 1860 München in 2013Personal informationDate of birth (1987-08-31) 31 August 1987 (age 36)Place of birth Zadar, SR Croatia, YugoslaviaHeight 1.84 m (6 ft 0 in)Position(s) WingerTeam informationCurrent team AstanaNumber 10Youth career NK Sv. Mihovil ZadarSenior career*Years Team Apps (Gls)2006–2009 Zadar 72 (12)2009–2012 Hajduk Split 76 (15)2012–2015 1860 München 51 (3)2015–2018 Rijeka 53 (16)2016–20...

منتخب إسكتلندا تحت 21 سنة لكرة القدم بلد الرياضة إسكتلندا الفئة كرة قدم تحت 21 سنة للرجال [لغات أخرى] رمز الفيفا SCO مشاركات تعديل مصدري - تعديل منتخب إسكتلندا تحت 21 سنة لكرة القدم هو الممثل الرسمي لـ اسكتلندا في بطولات كرة القدم تحت 21 سنة.[1][2][3&...

مجموعة دراسة الحركة التفاعلية الاختصار (بالروسية: ГИРД) البلد الاتحاد السوفيتي المقر الرئيسي موسكو تاريخ التأسيس 15 سبتمبر 1931 تاريخ الحل 1933 المدير سيرجي كوروليوففريدريك تساندريوري بابيدناستيف [لغات أخرى]ميخائيل تيخونرافوف تعديل مصدري - ...

Step bt Stepsingolo discograficoScreenshot tratto dal video del branoArtistaWhitney Houston Pubblicazione24 febbraio 1997 Durata4:12 Album di provenienzaColonna sonora di Uno sguardo dal cielo GenereContemporary R&BPop EtichettaArista Records ProduttoreStephen Lipson Registrazione1996 FormatiCD CertificazioniDischi d'oro Germania[1](vendite: 250 000+) Whitney Houston - cronologiaSingolo precedenteI Believe in You and Me(1996)Singolo successivoMy Heart Is Calling(199...

A typically wooden shaft used for playing cue sports A woman using a cue stick to push a billiard ball forward to move an object ball. A pool cue and its major parts.[1]: 71–72 [2] A cue stick (or simply cue, more specifically billiards cue, pool cue, or snooker cue) is an item of sporting equipment essential to the games of pool, snooker and carom billiards. It is used to strike a ball, usually the cue ball. Cues are tapered sticks, typically about 57–59&#...
Questa voce o sezione sull'argomento album pop non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Soggetti smarritialbum in studioArtistaRenato Zero Pubblicazione31 marzo 1986 Durata48:39 Dischi1 Tracce10 GenerePopFunk EtichettaZerolandia/RCA, PL 34387 ProduttoreRenato Zero e Piero Pintucci RegistrazioneLogi...

H-class submarine operated by the Royal Navy, This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2018) (Learn how and when to remove this message) HNLMS O 8 History United Kingdom NameHMS H6 BuilderCanadian Vickers, Montreal Laid down1914[1] Launched12 May 1915[1] Commissioned10 June 1915[1] FateSold to the Netherlands on 4 May 1917...

Freeman Dyson nel 2005 Premio Wolf per la fisica 1981 Freeman John Dyson (Crowthorne, 15 dicembre 1923 – Princeton, 28 febbraio 2020) è stato un fisico e matematico britannico naturalizzato statunitense, conosciuto principalmente per i suoi studi in elettrodinamica quantistica, fisica dello stato solido e ingegneria nucleare. Ha teorizzato vari concetti che portano il suo nome; i più importanti sono la trasformazione di Dyson, l'albero di Dyson, la serie di Dyson e la sfera di Dyson. Indi...

جزء من سلسلة مقالات حولالمطبخ العربي حسب البلد الجزيرة العربية البحرين الإمارات الكويت سلطنة عمان قطر السعودية اليمن المغرب الكبير الجزائر ليبيا موريتانيا المغرب تونس الشام العراق الأردن لبنان فلسطين سوريا نهر النيل مصر السودان القرن الأفريقي جيبوتي الصومال المحيط اله�...