Kappa calculus
|
Read other articles:

Chiaki MukaiKebangsaanJepangPekerjaanDokterKarier luar angkasaAntariksawan NASDA/JAXAWaktu di luar angkasa23 hari 15 jam 39 menitSeleksiGrup NASDA 1985MisiSTS-65, STS-95Lambang misi Chiaki Mukai, M.D., Ph.D. (向井千秋code: ja is deprecated , Mukai Chiaki, lahir 6 Mei 1952) adalah antariksawan NASDA sekaligus astronaut wanita pertama Jepang. Ia adalah dokter spesialis bedah lulusan Universitas Keio. Pendidikan Chiaki Mukai dilahirkan sebagai Chiaki Naito (内藤千秋code: ja is deprecate...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of World Heritage Sites in Serbia di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat...

United States historic placeJohn Turn FarmU.S. National Register of Historic Places John Turn Farm barn, HABS photo, 1970Show map of PennsylvaniaShow map of the United StatesLocationNortheast of Stroudsburg, Middle Smithfield Township, PennsylvaniaCoordinates41°3′30″N 75°1′25″W / 41.05833°N 75.02361°W / 41.05833; -75.02361Area6 acres (2.4 ha)Built byTurn, John, Sr.NRHP reference No.79000249[1]Added to NRHPJuly 23, 1979 John Turn Farm...

Untuk kegunaan lain, lihat Dunia (disambiguasi). Kelereng Biru Bumi. Dunia, buana, jagat, atau rat adalah nama umum yang digunakan untuk menyebut keseluruhan peradaban manusia, pengalaman manusia, sejarah manusia, atau keadaan manusia secara umum di seluruh Bumi,[1] atau mengenai segala sesuatu yang terdapat di dalamnya. Dalam konteks filosofi, dunia bisa merujuk pada keseluruhan fisik alam semesta, atau sebuah konsep ontologi. Dalam konteks teologi, dunia biasanya mengacu pada materi...
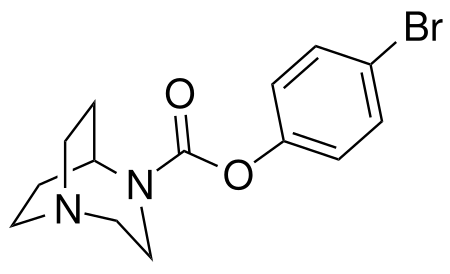
Chemical compound SSR-180,711Identifiers IUPAC name (4-bromophenyl) 1,4-diazabicyclo[3.2.2]nonane-4-carboxylate CAS Number298198-52-4 YPubChem CID9928899ChemSpider7973126UNIIQF4P1U1666Chemical and physical dataFormulaC14H21BrN2O2Molar mass329.238 g·mol−13D model (JSmol)Interactive image SMILES c1cc(ccc1OC(=O)N2CCN3CCC2CC3)Br InChI InChI=1S/C14H17BrN2O2/c15-11-1-3-13(4-2-11)19-14(18)17-10-9-16-7-5-12(17)6-8-16/h1-4,12H,5-10H2Key:RXLOZRCLQMJJLC-UHFFFAOYSA-N (verify) SSR...

Kris WuWu pada tahun 2017Nama asal吴亦凡LahirLi Jiaheng (李嘉恒)6 November 1990 (umur 33)Guangzhou, TiongkokKebangsaanKanadaNama lainWu Yi FanAlmamaterSir Winston Churchill Secondary SchoolPekerjaanPenyanyipenulis laguaktormodelTahun aktif2012–sekarangKarier musikAsalSeoul, Korea SelatanGenreHip hopR&BInstrumenVokalLabelAce Unit CultureInterscopeUniversal Music ChinaGo EastSMArtis terkaitExoExo-MSM Town Kris Wu Li Jiaheng Hanzi sederhana: 李嘉恒 Hanzi tradi...

Sulawesi Selatan IIIDaerah Pemilihan / Daerah pemilihanuntuk Dewan Perwakilan RakyatRepublik IndonesiaWilayah Daftar Kabupaten : Enrekang Luwu Luwu Timur Luwu Utara Pinrang Sidenreng Rappang Tana Toraja Toraja Utara Kota : Palopo ProvinsiSulawesi SelatanPopulasi2.679.554 (2023)[1]Elektorat1.920.090 (2024)[2]Daerah pemilihan saat iniDibentuk2009Kursi7Anggota La Tinro La Tunrung (Gerindra) Sarce Bandaso Tandiasik (PDI-P) Muhammad Fauzi (Golkar) ...

Swiss road cyclist Michael SchärSchär at the 2012 Critérium du DauphinéPersonal informationFull nameMichael SchärBorn (1986-09-29) 29 September 1986 (age 37)Geuensee, Lucerne, SwitzerlandHeight1.98 m (6 ft 6 in)Weight78 kg (172 lb; 12 st 4 lb)Team informationCurrent teamLidl–TrekDisciplineRoadRoleRider (retired)Directeur sportifRider typeDomestiqueAmateur team2006Hadimec Professional teams2006Phonak2007–2009Astana2010–2020BMC R...

История Грузииსაქართველოს ისტორია Доисторическая Грузия Шулавери-шомутепинская культураКуро-араксская культураТриалетская культураКолхидская культураКобанская культураДиаухиМушки Древняя история КолхидаАриан-КартлиИберийское царство ФарнавазидыГруз�...

Halaman ini memuat daftar paroki di Keuskupan Agung Palembang. Daftar ini tidak dimaksudkan sebagai suatu daftar yang lengkap atau selalu terbarui. Jika Anda melihat artikel yang seharusnya tercantum di sini, silakan sunting halaman ini dan tambahkan pranala ke artikel tersebut. Gunakan perubahan terkait untuk melihat perubahan terbaru dari artikel-artikel yang tercantum pada halaman ini.[1] Daftar Dekanat I Gambar Paroki Pelindung Lokasi Stasi/Kapel Paroki Katedral Palembang Santa Ma...

Suku Dayak MeratusDaerah dengan populasi signifikanKalimantan Selatan: 35.838 (BPS - sensus th. 2000) Kalimantan TimurBahasaMeratus, Banjar, IndonesiaAgama • Kaharingan, Kristen dan KatolikKelompok etnik terkaitDayak Ngaju, Banjar Litografi berjudul Orang-Boekit uit de Afdeeling Amoentai en Dajaksche vrouw uit Longwai (Orang Bukit dari afdeeling Amuntai dan wanita Dayak Modang dari Long Wai) berdasarkan gambar oleh Carl Bock (1887) Suku Dayak Meratus adalah nama kolektif untuk sekumpu...

Class of polyethylenes HDPE has SPI resin ID code 2 High-density polyethylene (HDPE) or polyethylene high-density (PEHD) is a thermoplastic polymer produced from the monomer ethylene. It is sometimes called alkathene or polythene when used for HDPE pipes.[1] With a high strength-to-density ratio, HDPE is used in the production of plastic bottles, corrosion-resistant piping, geomembranes and plastic lumber. HDPE is commonly recycled, and has the number 2 as its resin identification cod...

Chief queen consort of Burma Hanthawaddy Mibaya ဟံသာဝတီ မိဖုရားChief queen consort of BurmaTenure10 November 1581 – 19 December [O.S. 9 December] 1599PredecessorSanda DewiSuccessorThiri Maha Dhamma Yaza Dipadi DewiBornc. 1536 c. 898 METoungoo (Taungoo)DiedJune 1606 1st Waso 968 METoungooSpouseNanda BayinIssue1. Thakin Gyi[1] 2. Min Htwe (daughter) 3. Mingyi Swa 4. Khin Ma Hnaung (daughter) 5. Khin Pu (daughter) 6. Minye Kyawswa II 7. Tha...

Former Spanish colony in the Caribbean Spanish SantiagoSantiago1509–1655 FlagStatusColony of Spain; part of the Spanish West Indies, Captaincy General of Santo DomingoCapitalVilla de la VegaCommon languagesSpanishTaínoGovernment• King of Spain Ferdinand II of Aragon (First) Charles II of Spain (Last) Governor • 1510–1514 Juan de Esquivel (First)• 1656–1660 Cristóbal Arnaldo Isasi (Last) History • Established 1509• Disestablished 1655 C...

American Air Force general (born 1942) This article is about the U.S. Air Force general. For other people with the same name, see Richard Myers (disambiguation). Richard MyersGeneral Richard Myers in 2002Born (1942-03-01) 1 March 1942 (age 82)Kansas City, Missouri, United StatesAllegianceUnited StatesService/branchUnited States Air ForceYears of service1965–2005RankGeneralCommands heldChairman of the Joint Chiefs of StaffVice Chairman of the Joint Chiefs of StaffNorth American Aer...

Годы 1979 · 1980 · 1981 · 1982 — 1983 — 1984 · 1985 · 1986 · 1987 Десятилетия 1960-е · 1970-е — 1980-е — 1990-е · 2000-е Века XIX век — XX век — XXI век 2-е тысячелетие XVIII век XIX век XX век XXI век XXII век 1890-е 1890 1891 1892 1893 1894 1895 1896 1897 1898 1899 1900-е 1900 1901 1902 1903 1904 1905 1906 1907 1908 1909 1910-е 1910 1911 1912 1913 1914 1915 1916 1...

André FranquinNegara Belgia AreaPenulisKarya terkenal'Spirou et Fantasio Gaston Lagaffe Idées noireshttp://www.tintin.com André Franquin (3 Januari 1924 – 5 Januari 1997) adalah seorang pemberi pengaruh dan artis di bidang komik yang berkebangsaan Belgia, di mana karyanya yang terkenal adalah Gaston dan Marsupilami, yang diciptakannya ketika ia bekerja di Spirou et Fantasio komic dari tahun 1947 hingga 1969, yang mana masa-masa itu adalah masa keemasan di bidang perkom...

الدوري الإسكتلندي الدرجة الرابعة 2014–15 تفاصيل الموسم الدوري الإسكتلندي الدرجة الرابعة [لغات أخرى] البلد المملكة المتحدة الدوري الإسكتلندي الدرجة الرابعة 2013–14 الدوري الإسكتلندي الدرجة الرابعة 2015–16 تعديل مصدري - تعديل الدوري الإسكتلندي الدرجة ...

A map of the Zuidvleugel, with The Hague in the north-west and Rotterdam in the south-east. Zuidvleugel (Dutch pronunciation: [ˈzœytˌfløːɣəl], literally south wing) is the band of cities and towns located along the southern wing of the Randstad in the Netherlands. It is that part of the Randstad that is located in the Province of South Holland. This developing conurbation extends around 60 kilometres from Dordrecht to Leiden. The two main focal points are the area around Rotter...

Place in Upper Carniola, SloveniaMartinj VrhMartinj VrhLocation in SloveniaCoordinates: 46°11′26.88″N 14°7′58.9″E / 46.1908000°N 14.133028°E / 46.1908000; 14.133028Country SloveniaTraditional RegionUpper CarniolaStatistical regionUpper CarniolaMunicipalityŽeleznikiElevation781.3 m (2,563.3 ft)Population (2002) • Total232[1] Martinj Vrh (pronounced [maɾˈtiːɱ ˈʋəɾx]; in older sources also Sveti Martinj Vrh,&...











































![{\displaystyle (\kappa x.f)\circ \operatorname {lift} _{\tau }(c)=f[c/x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd7abb4a97cac1b0ca1beba0ac15725baf91bcd7)
















